文章目录
- 贝塞尔曲线
- 1.伯恩斯坦多项式法
- 2.德卡斯特里奥算法(de Casteljau Algorithm)
- 贝塞尔曲面
- 实验结果
贝塞尔曲线
给出一系列点(一般称为控制点),贝塞尔曲线可以利用这些点得到一个平滑的曲线,贝塞尔曲线不是一个表达式,而是由一系列离散的点构成的(类似移动最小二乘法)。
贝塞尔曲线通常有两种求解方法:
1.伯恩斯坦多项式法
对于n阶贝塞尔曲线(有n+1个控制点)而言,贝塞尔曲线上的点B(t):

2.德卡斯特里奥算法(de Casteljau Algorithm)
这种方法通过线性插值进行递归的方法求得贝塞尔曲线上的点。
贝塞尔曲线上的点
P
i
,
j
(线性插值)
P_{i, j}(线性插值)
Pi,j(线性插值):
P
i
,
j
=
(
1
−
t
)
P
i
−
1
,
j
+
t
P
i
−
1
,
j
+
1
P_{i, j}=(1-t) P_{i-1, j}+t P_{i-1, j+1}
Pi,j=(1−t)Pi−1,j+tPi−1,j+1
贝塞尔曲面
先由控制点得到的贝塞尔曲线的点P,对点P再进行贝塞尔曲线就得到了贝塞尔曲面。
实验结果
控制点

贝塞尔曲线
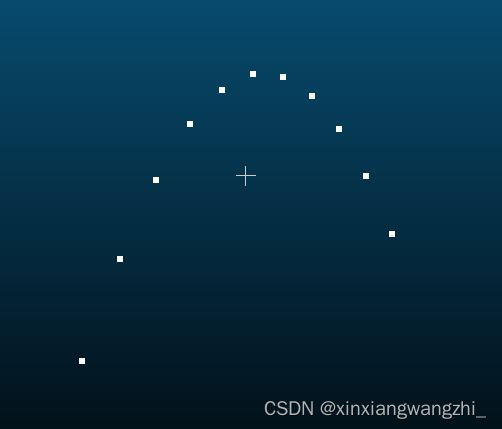
曲面控制点

贝塞尔曲面

参考链接:
1
2
3