前面的顺序表是顺序存储（类似于数组），下面的链表是链式存储。物理是否相邻就看其存储地址（格子）是否相邻挨在一起。逻辑是否相邻看其前驱后继。

例如上面3个数据

如果存在顺序表中，那就是100的后继是200,200的后继是150，有100,200,150三个格子的有效数据，且这三个格子是按前驱，后继有序的相连着，这就是逻辑相邻。而格子的地址挨在一起就是物理相邻。如下图，3个格子挨在一起

如果存在链表中，那么每个格子的前驱，后继都不变也就是仍然逻辑相邻，100的后继还是200，但200的这个格子地址就不一定和100的格子地址挨在一起了。200的格子地址可能比100的格子地址大，也可能比100的格子地址小，其在哪里都有可能。

那要寻找100的后继200这个数字要怎么找——

前面顺序表找后继可以直接用下标i，因为其地址是相邻挨在一起的。

而在链表里面，你也不知道地址在哪里，那么就需要一开始就把它的地址标记起来。

那么链表里的格子就要再加一个东西，在每一个当前数据格子的下面再加一层，将当前数据的后继数据的地址存在里面。（当前数据，后继地址）

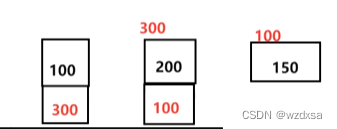
假设现在150是最后一个数据，按理说150的下面应该登记写上它下一个数据的地址，但150后面没有下一个数据了，所以150的下面就应该写一个空(NULL).表示其为末尾元素，没有后继了。

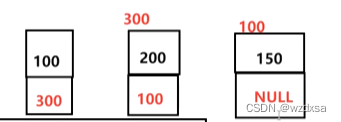
现在单链表的形式就成了，保存了地址为300，就指向地址为300的数据200，保存了地址为100，就指向地址为100的数据150，保存地址为空，就完了。

那么单链表的结构就长成这个样子

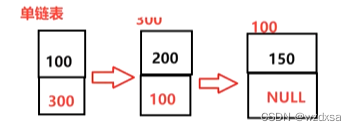
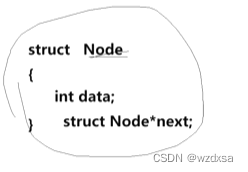
现在来看图写话，写出单链表的结构体struct Node，包含2个成员，整型数据类型的数据（名为date）和单链表结构体类型的指针（名为next）。

（（*）为指针，其前面写的为指针的类型，即指针指向的东西的数据类型是什么，后面写的为指针的名字，先给指针起个名字叫next，就是下一个地址的意思；而指针的类型还是跟它一样的struct Node，因为它指向单链表中的下一组跟它当前的结构样子是长的一样的，单链表中每一组都包含2个成员，数据和指针。而跟它长相一样的结构就又还是定义了的struct Node）。如图

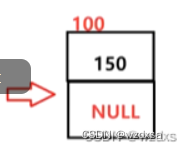
所以单链表的结构体设计就长成这样

现在来分析一下这个单链表带不带头结点——

头结点就是用来指向表中的第一个数据。因为如果要访问单链表中这一串数据，要先指向第一个数据后，再通过其下面的指针访问每个后继。

所以需要一个头指针（即头结点）指向第一个数据的存储地址。

假设这个头指针的名字叫plist,那么通过plist所指的地方，就能找到第一个数据100。接着再访问每个后继，直到后继为空，则前面找到的所有数据就是单链表里面所存储的数据。

那么现在单链表就是长成这个样子

接下来在这种形式的单链表中，数据应该怎么插入——

例如在100前面插入一个数据10，插入完后的样式应该是这样

那么现在plist就要指向数据10的地址，因为10变成了第一个数据，然后数据10的next指向数据100的地址。

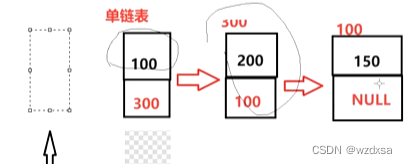
现在plist就要从指向100的地址改变为指向10的地址，也就是plist指针指向变了。C语言里面学过要改变指针的指向需要——传指针解引用。而plist本身就是一个指针，再传指针就变成了二级指针。同理删除是直接穿过要删除的数据指向下一个数据，也要改变指针方向。但二级指针就更复杂一些

所以需要一个做任何操作都永远不改变plist指向的方法，让plist一直指向头结点——加一个头结点，这个头结点里面的数据永远不用，不算作第一个数据，也就是头结点里没有不放数据。真正的有效数据从头结点的下一个节点开始，也就是100仍然是第一个数据，头结点的next指向第一个有效数据的地址。

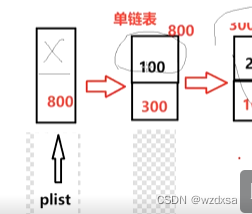
现在要往100前面插入数据或是直接删除数据100，plist都不用改动，只改变头结点的next指向就好了。

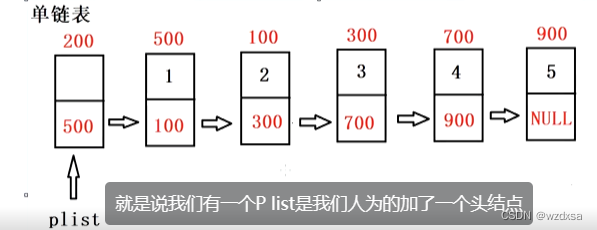
所以上图就是单链表的最终结构设计，单链表的处理必须要带有头结点。这里plist指向头结点的地址200.在对第一个数据结点做任何操作时它都不会变。

 而其实现函数跟顺序表差不多，因为它们都属于——线性表。线性表分为顺序存储和链式存储。

链式存储就是这个单链表。