前缀和与差分算法：

  前缀和与差分算法主要是为了快速求出某个区间的和，例如有一个数组a[10]={0，1，2，3，4，5，6，7，8，9}，我们需要求a[3]到a[7]的和，传统的办法是求a[3]+a[4]+a[5]+a[6]+a[7]，但是这样求复杂度是O(n)，如果我们建立了一个前缀数组S[9]={a[0]，a[0]+a[1]，a[0]+a[1]+a[2]，a[0]+a[1]+a[2]+a[3]，……，a[0]+a[1]+……+a[9]}，那么我们要求a[3]到a[7]的和可以用差分思想S[7]-S[2]即可求出

1、校门外的树

NC16649 校门外的树

题目描述
  某校大门外长度为L的马路上有一排树，每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴，马路的一端在数轴0的位置，另一端在L的位置；数轴上的每个整数点，即0，1，2，……，L，都种有一棵树。

  由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的树（包括区域端点处的两棵树）移走。你的任务是计算将这些树都移走后，马路上还有多少棵树。

输入描述:
  第一行有两个整数：L（1 <= L <= 10000）和 M（1 <= M <= 100），L代表马路的长度，M代表区域的数目，L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数，用一个空格隔开，表示一个区域的起始点和终止点的坐标。

输出描述:
  包括一行，这一行只包含一个整数，表示马路上剩余的树的数目。

示例1
输入
500 3
150 300
100 200
470 471

输出
298

备注:
对于20%的数据，区域之间没有重合的部分；
对于其它的数据，区域之间有重合的情况。

解题思路：
下面通过样例来解释
输入
10 3
2 5
3 6
8 8

输出
5

1、一个数组初始化为0，a[11]={0}，左边界+1，右边界后1格-1

2、例如2 5，那么a[2]++,a[6]–，3 6，那么a[3]++，a[7]–，8 8，那么a[8]++,a[9]–，处理完后结果如下：

a[0]	a[1]	a[2]	a[3]	a[4]	a[5]	a[6]	a[7]	a[8]	a[9]	a[10]
0	0	1	1	0	0	-1	-1	1	-1	0

进行前缀和后：

a[0]	a[1]	a[2]	a[3]	a[4]	a[5]	a[6]	a[7]	a[8]	a[9]	a[10]
0	0	1	2	2	2	1	0	1	0	0

a[i]代表的值就是被移走的次数，可见a[0]，a[1]，a[7]，a[10]没有被移走，答案是4

3、模拟上面过程即可

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,m;
    cin>>n>>m;
    int a[10010]={0};
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        a[x]++;//起点+1
        a[y+1]--;//终点-1
    }
    int ans=0;
    for(int i=0;i<=n;i++){//从0到n
        if(i){//前缀和
            a[i]+=a[i-1];
        }
        if(a[i]==0){//没有被移走的
            ans++;
        }
    }
    cout<<ans<<endl;
}

2、值周

NC24636 值周

题目背景
你是能看见第3题的friends哦 ——taoyc

题目描述
  JC内长度为L的马路上有一些值周同学，每两个相邻的同学之间的间隔都是1米。我们可以把马路看成一个数轴，马路的一端在数轴0的位置，另一端在L的位置；数轴上的每个整数点，即0,1,2,…L，都有一个值周同学。 由于水宝宝有用一些区间来和ssy搞事情，所以为了避免这种事走漏风声，水宝宝要踹走一些区域的人。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的人（包括区域端点处的两个人）赶走。你的任务是计算将这些人都赶走后，马路上还有多少个人。

输入描述:
  第一行有2个整数L和M，L代表马路的长度，M代表区域的数目，L和M之间用一个空格隔开。 接下来的M行每行包含2个不同的整数，用一个空格隔开，表示一个区域的起始点和终止点的坐标

输出描述:
  1个整数，表示马路上剩余的人的数目。

示例1
输入
500 3
150 300
100 200
470 471

输出
298

说明
对于所有的数据，1≤L≤100000000
对于10%的数据，1<=M<=100
对于20%的数据，1<=M<=1000
对于50%的数据，1<=M<=100000
对于100%的数据，1<=M<=1000000

解题思路：
这题和第一题校门外的树做法是一模一样的，只是数据量的问题，第一用暴力做法也可以通过，这题必须要用前缀和做法降低时间复杂度，详解看第一题即可

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n,m;
    cin>>n>>m;
    int a[100000010]={0};
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        a[x]++;
        a[y+1]--;
    }
    int ans=0;
    for(int i=0;i<=n;i++){
        if(i){
            a[i]+=a[i-1];
        }
        if(a[i]==0){
            ans++;
        }
    }
    cout<<ans<<endl;
    
}

3、中位数图

NC19913 中位数图

题目描述
  给出1~n的一个排列，统计该排列有多少个长度为奇数的连续子序列的中位数是b。中位数是指把所有元素从小到大排列后，位于中间的数。

输入描述:
第一行为两个正整数n和b ，第二行为1~n 的排列。

输出描述:
输出一个整数，即中位数为b的连续子序列个数。

示例1
输入
7 4
5 7 2 4 3 1 6

输出
4

备注:
对于30%的数据中，满足 n≤100；
对于60%的数据中，满足 n≤1000；
对于100%的数据中，满足 n≤100000,1≤b≤n。

解题思路：
下面模拟样例
1、如果大于中位数，那么标记为1，如果等于，那么标记为0，小于标记为-1，样例的数组如下：

a[0]	a[1]	a[2]	a[3]	a[4]	a[5]	a[6]
1	1	-1	0	-1	-1	1

前缀和后：

a[0]	a[1]	a[2]	a[3]	a[4]	a[5]	a[6]
1	2	1	1	0	-1	0

2、我们以a[3]为中介点，因为从a[3]开始，区间开始包括了要求的中位数，a[0]~a[2]记录状态的数量，a[3]~a[n-1]用来计算答案

3、需要用一个map来储存a[3]之前各种状态的值，默认m[0]=1,那么最终值如下表

m[0]	m[1]	m[2]	m[3]
1	2	1	0

4、枚举到a[3]时，前缀和后a[3]的状态是1，那么ans+=m[1]，为什么呢？因为差分后如果状态是0，那么中位数就是要求的数，前缀和后a[0]=1,a[2]=1,a[3]=1，那么1~3,3~3都是符合要求的答案，a[4]=0,m[0]=1,那么ans+=m[0]，它的意思代表着*43，那个*有多少种方案，a[5]时，它的意思是*431，那个*有多少种方案

5、差分有点难理解，还是得靠自己揣摩，加油！

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,b;
    cin>>n>>b;
    int a[100010]={0};//a[i]的值为1时，代表a[i]原本的值大于1，为0时代表等于，-1代表小于
    unordered_map<int,int> m;//记录状态的数量
    m[0]=1;//状态0默认是1
    for(int i=0;i<n;i++){
        cin>>a[i];
        if(a[i]>b){
            a[i]=1;
        }else if(a[i]==b){
            a[i]=0;
        }else{
            a[i]=-1;
        }
    }
    int sum=0;
    int flag=1;
    long long ans=0;
    for(int i=0;i<n;i++){
        sum+=a[i];//前缀和
        if(a[i]==0){
            flag=0;
        }
        if(flag){//还没有包含则添加状态
            m[sum]++;
        }else{//包含了则计算答案
            ans+=m[sum];
        }
    }
    cout<<ans<<endl;
}

4、激光炸弹

NC20032 激光炸弹

题目描述
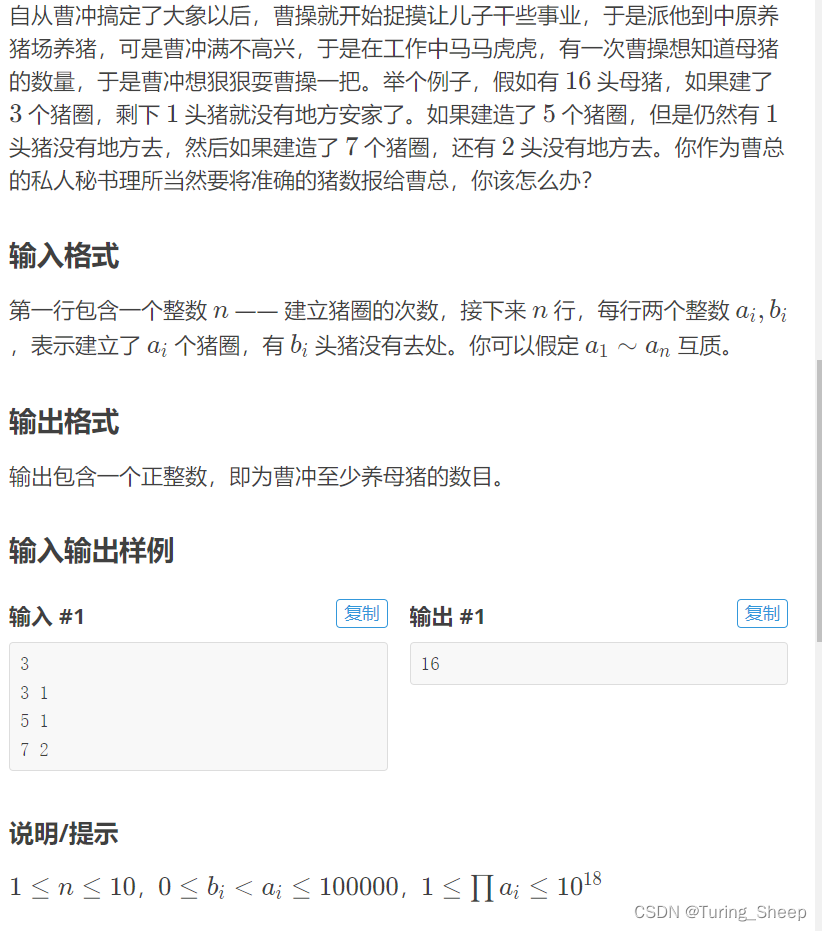
一种新型的激光炸弹，可以摧毁一个边长为R的正方形内的所有的目标。
现在地图上有n(N ≤ 10000)个目标，用整数X_i,Y_i(其值在[0,5000])表示目标在地图上的位置，每个目标都有一个价值。
激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆破范围，即那个边长为R的正方形的边必须和x，y轴平行。
若目标位于爆破正方形的边上，该目标将不会被摧毁。

输入描述:
输入文件的第一行为正整数n和正整数R，接下来的n行每行有3个正整数，分别表示 xi，yi ，vi 。

输出描述:
输出文件仅有一个正整数，表示一颗炸弹最多能炸掉地图上总价值为多少的目标（结果不会超过32767）。

示例1
输入
2 1
0 0 1
1 1 1

输出
1

解题思路：
该题是一道二维的前缀和与差分题目，要求一个矩形里各个元素的总和，下面解释示例1

1、用1个数组a[m][m]记录某个点的值
2、对a[m][m]进行前缀和，那么a[i][j]代表的意思是a[0][0],a[i][0],a[0][j],a[i][j]这个矩形的价值总和

3、通过差分快速求出每个符合条件的矩阵的总和，取最大值即可

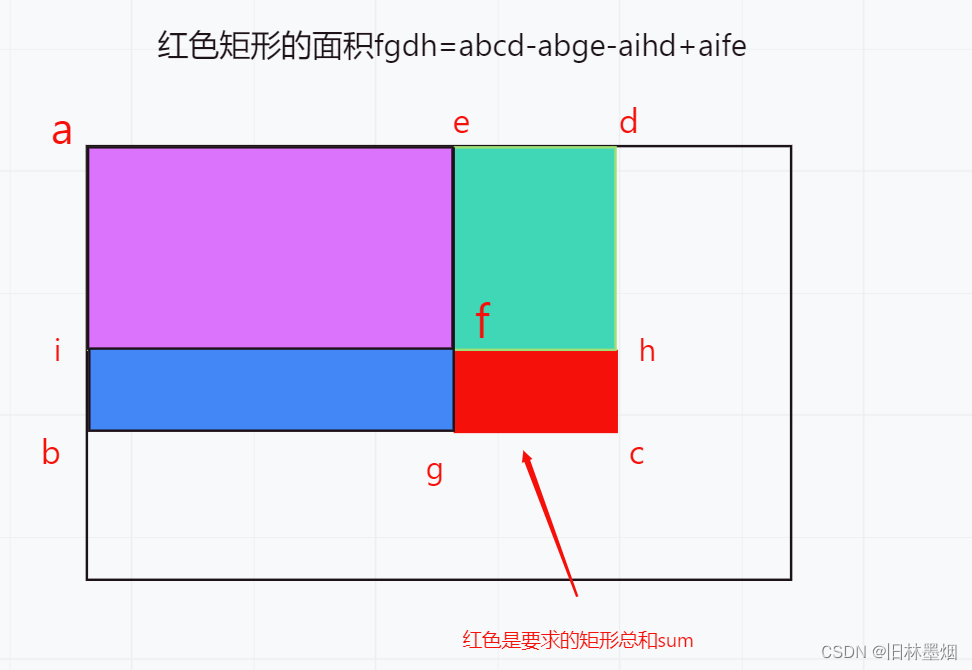
4、详细的前缀做法可以参考代码

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,m;
    cin>>n>>m;
    int a[5010][5010]={0};
    for(int i=0;i<n;i++){
        int x,y,v;
        cin>>x>>y>>v;
        a[x][y]=v;
    }
    int ans=0;
    for(int i=0;i<5010;i++){//进行前缀和
        for(int j=0;j<5010;j++){
            if(i!=0){
                a[i][j]+=a[i-1][j];
            }
            if(j!=0){
                a[i][j]+=a[i][j-1];
            }
            if(i!=0&&j!=0){
                a[i][j]-=a[i-1][j-1];
            }
        }
    }
    for(int i=0;i<5010;i++){//差分快速求解
        for(int j=0;j<5010;j++){
            int sum=a[i][j];
            if(i-m>=0){
                sum-=a[i-m][j];
            }
            if(j-m>=0){
                sum-=a[i][j-m];
            }
            if(i-m>=0&&j-m>=0){
                sum+=a[i-m][j-m];
            }
            ans=max(ans,sum);//取最大值
        }
    }
    cout<<ans<<endl;
    
}

5、二分

NC207053 二分

题目描述
  我们刚刚学了二分查找——所谓二分查找就是在一堆有序数里找某个符合要求的数。在学完二分查找之后如果让你玩猜数游戏（裁判选定一个目标数字，你说一个数裁判告诉你是高了还是低了直到你猜到那个数）的话，显然你会用二分的方式去猜。

  但是不是每一个玩猜数游戏的人都知道二分是最好，甚至一个健忘的玩家都有可能在得到裁判回答的下一个瞬间就忘了他之前问了什么以及裁判的回答），而现在更可怕的是，这个告诉你猜的数是高还是低的裁判他也很健忘，他总是薛定谔的记得这个目标数字，也就是说他的回答有可能出错。我们已经不关心这个不靠谱的游戏本身了，我们更关心裁判这个薛定谔的记得到底有几个是记得…
现在给出这个健忘的玩家的所有猜测和裁判的所有回答，问裁判最多能有多少次是记得目标数字的，即裁判的回复是符合情况的。

输入描述:
第一行包含一个正整数n，表示裁判的回答数（也是玩家的猜数次数）。
接下来n行，首先是猜的数，然后是一个空格，然后是一个符号。符号如果是“+”说明猜的数比答案大，“-”说明比答案小，“.”说明猜到了答案。

输出描述:
包含一个正整数，为裁判最多有多少个回答是正确的。

示例1
输入
4
5 .
8 +
5 .
8 -

输出
3

说明
当目标数组是5时，5 . 5 . 8 + 这三个回答都是正确的

备注:
n≤100000
所有数的大小都小于int类型最大值。

解题思路：
1、如果是x +，那么当正确的数m>x时该式子成立，如果是x .，那么当正确的数m=x时该式子成立，如果是x -，那么当正确的数m=x时该式子成立

2、题目要求的是尽可能多的式子成立，那么我们可以枚举出现过的数字，最优解一定在里面的，下面解释样例

3、样例只出现了5，8，那么我们只要判断这两个数字是正确的数字的时候的值，当正确的数为5时，3个式子成立，当正确的数为8时，1个式子成立，这里不太符合，但是保底最小成立数是1

4、如果直接用数组去做前缀和，那么空间复杂度是int的最大值，时间复杂度也是，显然是不理想的。需要用一个map去离散化数据，比如用ma[0]代表5，用a[1]代表8，a[0]=3，那么代表正确的数是5时，有三个式子成立，如果您对map不熟悉，可以看我的另一篇文章：

c++ map用法 入门必看 超详细

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    cin>>n;
    map<int,int> a;//map可以按键值升序排序，并且可以离散化数据
    int b[100010]={0};
    for(int i=0;i<n;i++){
        int c;
        string s;
        cin>>c>>s;
        if(s=="+"){
            a[0]++;
            a[c]--;
        }
        if(s=="-"){
            a[c+1]++;
        }
        if(s=="."){
            a[c]++;
            a[c+1]--;
        }
    }
    int ans=0;
    int k=0;
    for(auto c:a){//离散化后转回数组
        b[k++]=c.second;
    }
    for(int i=0;i<100010;i++){
        if(i){//前缀和
            b[i]+=b[i-1];
        }
        ans=max(ans,b[i]);//取最优答案
    }
    cout<<ans<<endl;
}

6、货仓选址

NC50937 货仓选址

题目描述
  在一条数轴上有N家商店，它们的坐标分别为 A[1]~A[N]。现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入描述:
第一行一个整数N，第二行N个整数A[1]~A[N]。

输出描述:
一个整数，表示距离之和的最小值。

示例1
输入
4
6 2 9 1

输出
12

备注:
对于100%的数据:N≤100000, A[i]≤1000000

解题思路：
货仓选址问题是非常经典的题目，下面给出结论，可以自己推敲一下

1、如果货仓个数是奇数个，那么建在中位数那里是最优的，如果是偶数，那么建在两个中位数中间任意一定是最优的，例如样例，个数为偶数，那么建在2和6之间是最优的

2、我们可以通过sort排序取得中位数，也可以用nth_element直接求出中位数，如果对这两个函数不熟的话可以看我另外的一篇文章

c++入门必学库函数 sort
c++ nth_element()函数

代码：

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n;
    int a[100010]={0};
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    nth_element(a,a+n/2,a+n);//找到第i大的数，n/2大的数也就是中尾数
    int m=a[n/2];
    int ans=0;
    for(int i=0;i<n;i++){
        ans+=abs(m-a[i]);//其它点到该点的距离
    }
    cout<<ans<<endl;
}

是不是很简单呢？

刚接触肯定会觉得难，多些做题多些用，熟悉了就容易了，兄弟萌，加油！！！

文章尚有不足，欢迎大牛们指正

感谢观看，点个赞吧