一.首符号集(First())
技巧:找最左边可能出现的终结符
例:

1.First(E)
E->T
,最左边为T,又因为T->F
,最左边为F,F->(E)|i,则最左边为{(,i }
2.First(T):只需要看符号串最左边的符号,即=First(T)
T->F
,最左边为F,F->(E)|i,则最左边为{(,i }
3.First((E)):也只需要看最左边的
First((E))={ ( }
4.First(i):终结符的first集就是它本身
First(i)={i}
其他以此类推:

二.后跟符号集(Follow()):只针对非终结符
技巧:看”->“的右边,找出非终结符后面所能跟随的所有终结符
1. # Follow (S),S为识别符号,即 ”#“要放在开始符号"S"的 Follow集中
2.若存在规则U->xWy,First(y)-{}(空串)
Follow(W)
3.若存在规则U->xW或U->xWy,其中y能广义推导出(空串),则Follow(U)
Follow(W)

Follow(E)
首先E是开始符号,Follow(E)={#}
在"->"右边找E,看E后面跟的所有终结符号,这里F->(E)| i,E的右边为")",终结符的First集就是它本事(对应第二条规则)
所以Follow(E)={#,)}
Follow(T)
首先找”->“的右边,看T后面跟的所有终结符号
E->T
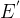
->+T
|
T后面跟的是
,
的First集是{+,
},将
去掉,最后得到{+},又因为
可以推导出
空串(对应第三条规则),就要把
E->T
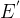
->+T
|
”->“左边的E和
的follow集写上
Follow(T)={+,#,)}
Follow(E‘)
首先找”->“的右边,看E’后面跟的所有终结符号
E->T
->+T
|
后面没有符号,
的follow集就是”->“左边E和
的follow集
Follow(
)={#,)}
以此类推:

总结
在"->"右边寻找需要求的非终结符,如果非终结符后面是终结符号,直接放到follow集中,如果非终结符后面是非终结符,就看非终结符的first集内容是什么,如果有
(空串)
1.那么将空串去掉写入follow集中
2.并且将”->“左边的非终结集的follow集也写入该follow集中
3. 选择符号集:Select(A->)
约束:有两条或两条以上产生式才算可选集
E->TE' 不用算可选集
E‘->+TE'|
算可选集
规则:
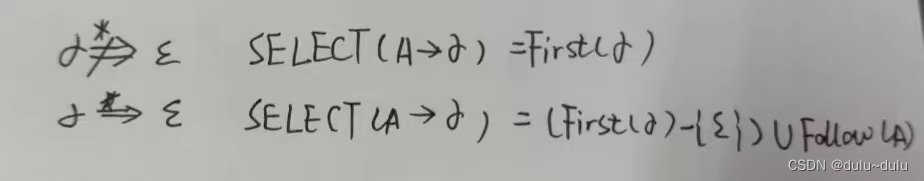
Select (E'->+TE')
根据规则,不能广义推导出
,那么运用第一条规则
Select (E'->+TE')={+}
Select(E'->)
运用第二条规则,”->“右边的首符号集-空串(这里-
后为空集),再并上E’的follow集
Select(E'->
) ={#,)}
Select(T'->+FT')
”+"号的首符号集就是”+“,所以
Select(T'->+FT')={+}
以此类推: