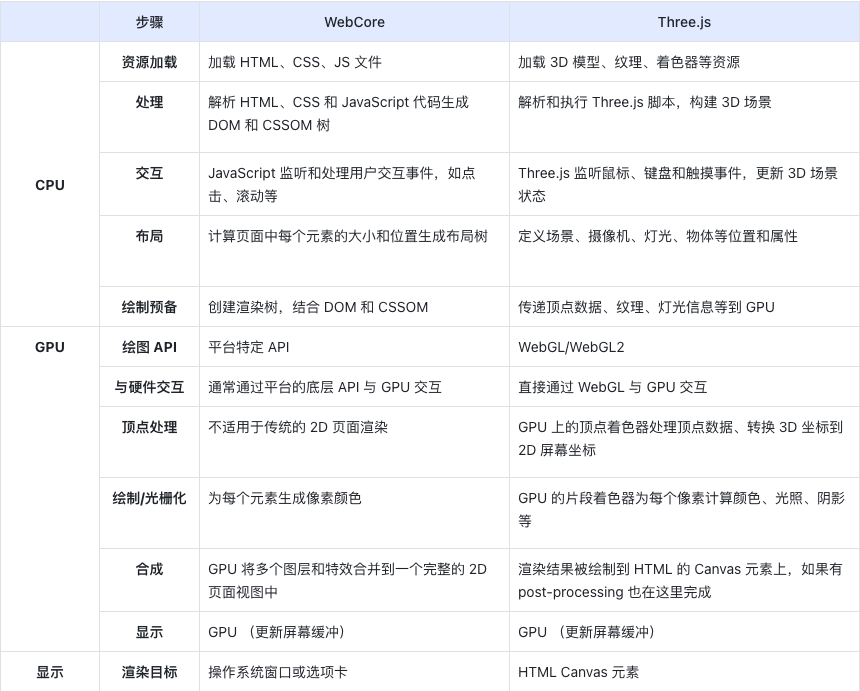
题面
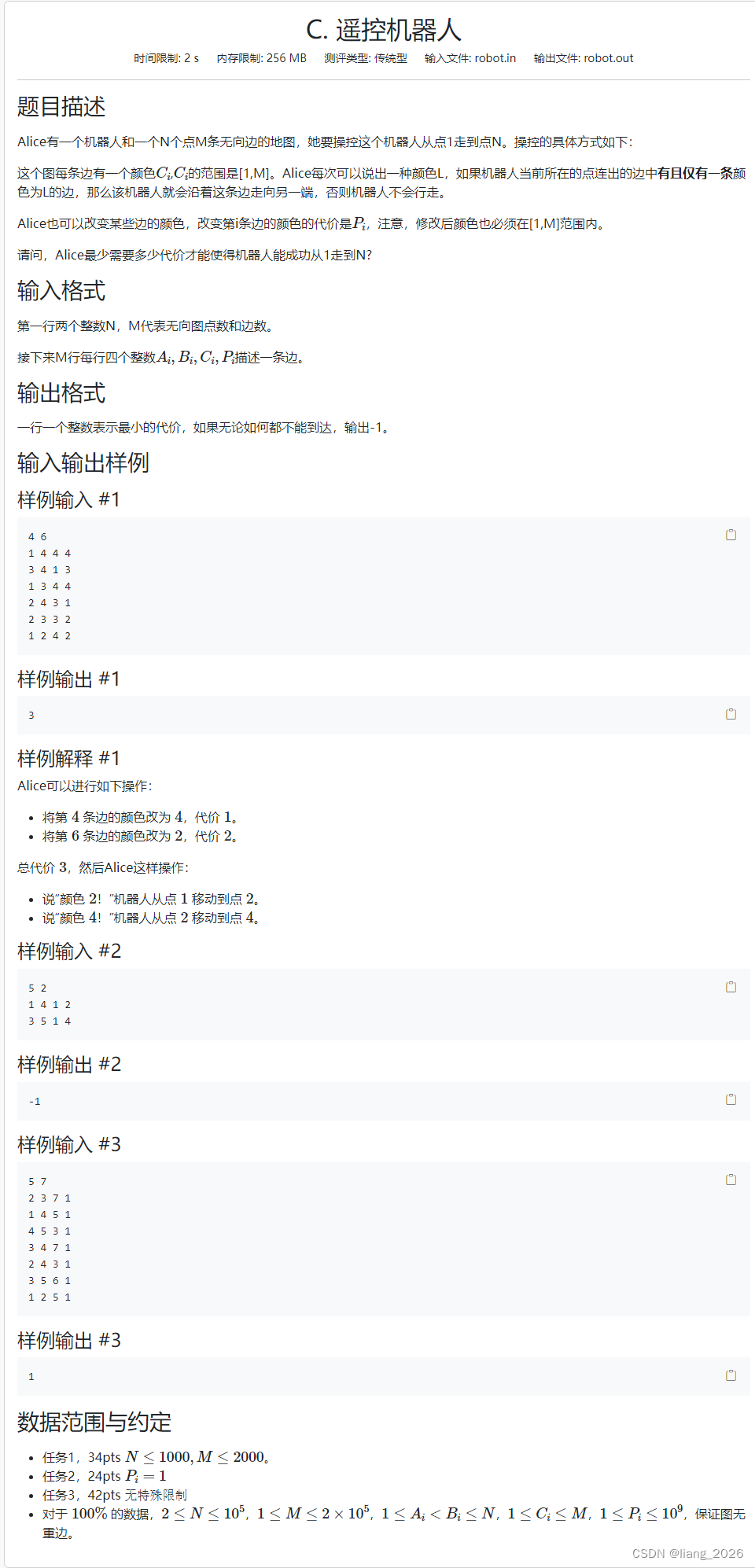
简要题意:
给你一个
n
n
n 个点
m
m
m 条边的图。边
i
i
i 有颜色
c
i
c_i
ci。你可以选择一些边改变它们的颜色成为区间
[
1
,
m
]
[1, m]
[1,m] 中的任意颜色,改变一条边
i
i
i 一次的代价是
w
i
w_i
wi。询问你能否在一些改变操作后使得可以从
1
1
1 号点,每次只经过当前点的 特殊边 到达
n
n
n。特殊边的定义是 对于当前点而言,特殊边的颜色在该点所有出边中有且仅出现一条。 如果可以,输出最小代价。否则输出
−
1
-1
−1。
分析:
凭感觉是一道最短路的题。
首先有一个性质:因为颜色的区间与边数相同,所以如果要改变一条边,那么可以把它变成一个任何别的边都不会再变成的颜色。换言之, 如果要花费代价改变某一条边的颜色,那么可以把它变成无色,并且这样是最优的。
接下来我们考虑如果一条边 ( u , v ) (u, v) (u,v) 的颜色是 c c c,花费是 w w w。我们从 u u u 到 v v v 经过它花费代价有几种情况:
1. u u u 的出边中是 c c c 颜色的只有一条,那么代价是 0 0 0。
2. u u u 的出边中 c c c 颜色的边有多条,改变这条边的颜色至无色,花费是 w w w。
3.
u
u
u 的出边中
c
c
c 颜色的边有多条,改变不改变它的颜色,改变其它边的颜色至无色。
花费是
v
a
l
u
,
c
−
w
val_{u, c} - w
valu,c−w。
v
a
l
u
,
c
val_{u, c}
valu,c 代表所有
u
u
u 的出边中颜色是
c
c
c 的边的代价之和。
不难发现,情况 1 1 1 可以归到情况 3 3 3 中。
我们考虑把这两种代价看做两种边权跑最短路会有什么问题:
如果按照情况
3
3
3 从
u
u
u 到
v
v
v,我们考虑会不会存在一个问题:按照情况
3
3
3 我们需要把其它颜色也为
c
c
c 的边都改成无色,那么把它变成无色但是却不记录会不会影响后面答案的计算呢?
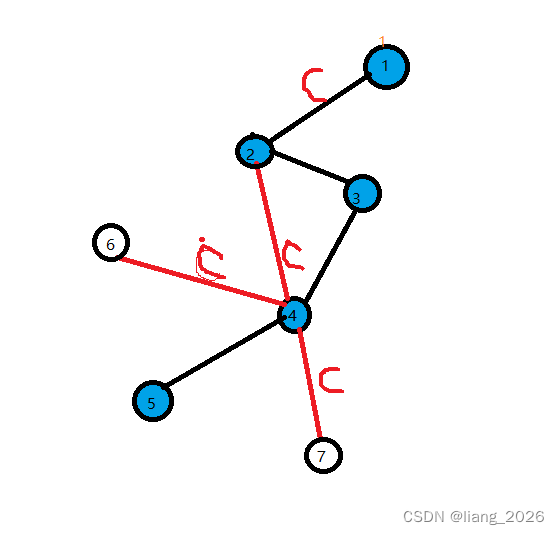
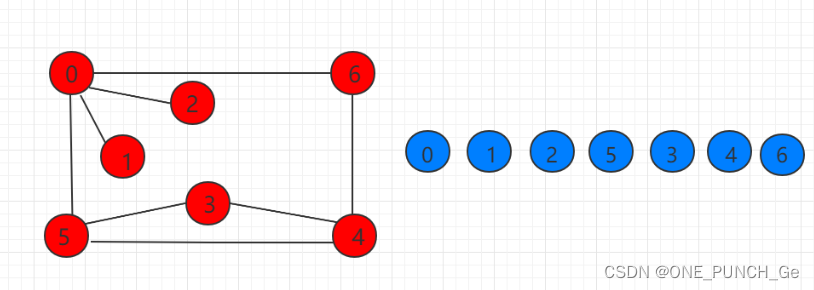
蓝色点表示最优路径的点,红色的边表示情况 3 3 3 中染成无色的边,它们的颜色是 c c c。黑色的边表示最优路径的边。那么如果出现上图的情况(从 5 5 5 号点走到 1 1 1 号点),那么 2 2 2 号点到 1 1 1 号点似乎是不需要花费的,因为在从 4 4 4 号点到 3 3 3 号点的时候就把那条颜色为 c c c 的边染成了无色。但是我们按照上面的规则进行的话,如果从 2 2 2 到 3 3 3 还使用情况 3 3 3,显然会多算一个代价。
但是深入思考一下,这种情况不会发生。因为这样的路径一定不是最优路径。如果按照上图的走法,那么 ( 2 , 4 ) (2,4) (2,4) , ( 6 , 4 ) (6, 4) (6,4), ( 4 , 7 ) (4, 7) (4,7) 的代价都会被算。实际上如果我们直接选择路径 5 → 4 → 2 → 1 5 \to 4 \to 2 \to 1 5→4→2→1,并且 ( 4 , 2 ) (4, 2) (4,2) 使用情况 2 2 2, ( 2 , 1 ) (2, 1) (2,1) 使用情况 3 3 3 肯定更加优秀。
这也就意味着: 如果我们能够通过某种方式处理好情况 2 2 2 带来的影响(即把边染成无色的影响),那么按照上面的规则跑最短路就是对的。
如果按照情况 2 2 2 经过一条颜色为 c c c 的边 从 u u u 到 v v v,那么 ( u , v ) (u, v) (u,v) 这条边颜色的改变可能会影响从 v v v 到 k k k 经过一条颜色为 c c c 按照情况 3 3 3 所花费的代价。根据这个问题,我们考虑 拆点。
有一个很暴力的想法是我们把每一个点拆成 m + 1 m + 1 m+1 个点:若有三个点 a a a, b b b , c c c。 a a a 到 b b b 经过一条颜色为 x x x 的边,当使用情况 2 2 2 的时候,可以从 a a a 走向 b x b_x bx,代价为 0 0 0, b x b_x bx必须继续沿着颜色x使用情况 3 3 3 走向其他点。每一个点的 0 0 0 状态表示 没有限制。这样我们就解决了维护信息的问题。但是复杂度好像有点问题。
我们考虑实际上一个点没有必要开 m m m 个点,只需要对每个点开其存在的颜色数个点就行了。一条边能够提供给两个点分别提供 1 1 1 个点,所以总点数是 2 m + n 2m + n 2m+n。然后建图跑最短路即可。时间复杂度 O ( ( n + m ) l o g 2 ( n + m ) ) O((n + m)log_2(n + m)) O((n+m)log2(n+m))。常数有亿点大。
CODE:
#include<bits/stdc++.h>//拆点 把点的状态拆一下
using namespace std;
const int N = 1e5 + 10;
const int M = 2e5 + 10;
const int T = 2 * N + M * 2;
typedef pair< int, int > PII;
typedef long long LL;
inline int read(){
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){if(c == '-') f = -1; c = getchar();}
while(isdigit(c)){x = (x << 1) + (x << 3) + (c ^ 48); c = getchar();}
return x * f;
}
int u, v, c;
int n, m, head[T], ut[M], vt[M], ct[M], tot, len;//最多T个点
bool vis[T];
LL wt[M], dis[T], res, w;
map< PII, int > rk;
map< PII, LL > val;
struct edge{
int v, last;
LL w;
}E[M * 8 + 10000];
void add(int u, int v, LL w){
E[++len].v = v;
E[len].last = head[u];
E[len].w = w;
head[u] = len;
}
struct state{
int x; LL w;
friend bool operator < (state a, state b){
return a.w > b.w;
}
};
void dijkstra(int s){
priority_queue< state > q;
q.push((state){s, 0});
while(!q.empty()){
state u = q.top(); q.pop();
int x = u.x;
if(vis[x]) continue;
vis[x] = 1;
for(int i = head[x]; i; i = E[i].last){
int v = E[i].v; LL w = E[i].w;
if(dis[v] > dis[x] + w){
dis[v] = dis[x] + w;
q.push((state){v, dis[v]});
}
}
}
}
int main(){
n = read(), m = read();
for(int i = 1; i <= n; i++){
rk[make_pair(i, 0)] = ++tot;
}
for(int i = 1; i <= m; i++){
u = read(), v = read(); c = read(), w = 1LL * read();
if(!rk[make_pair(u, c)]) rk[make_pair(u, c)] = ++tot;
if(!rk[make_pair(v, c)]) rk[make_pair(v, c)] = ++tot;
val[make_pair(u, c)] += w;
val[make_pair(v, c)] += w;
ut[i] = u, vt[i] = v, wt[i] = w, ct[i] = c;
}
for(int i = 1; i <= m; i++){
int u = ut[i], v = vt[i], c = ct[i], w = wt[i];
add(rk[make_pair(u, 0)], rk[make_pair(v, 0)], w);//改变颜色,不做限制
add(rk[make_pair(u, 0)], rk[make_pair(v, c)], 0);//改变颜色,必须限制
add(rk[make_pair(u, c)], rk[make_pair(v, 0)], val[make_pair(u, c)] - w);
add(rk[make_pair(u, 0)], rk[make_pair(v, 0)], val[make_pair(u, c)] - w);
add(rk[make_pair(v, 0)], rk[make_pair(u, 0)], w);//改变颜色,不做限制
add(rk[make_pair(v, 0)], rk[make_pair(u, c)], 0);//改变颜色,必须限制
add(rk[make_pair(v, c)], rk[make_pair(u, 0)], val[make_pair(v, c)] - w);
add(rk[make_pair(v, 0)], rk[make_pair(u, 0)], val[make_pair(v, c)] - w);
}
memset(dis, 0x3f, sizeof dis);
dis[rk[make_pair(1, 0)]] = 0;
dijkstra(rk[make_pair(1, 0)]);
res = dis[rk[make_pair(n, 0)]];
if(res == 0x3f3f3f3f3f3f3f3f) res = -1;
printf("%lld\n", res);
return 0;
}

![[移动通讯]【Carrier Aggregation-13】【Carrier Aggregation】](https://img-blog.csdnimg.cn/aa81d55d3f7e4e5eb946ce6203561378.png)