[python 刷题] 437 Path Sum III

之前有写过 Path Sum I & II, leetcode 112 & 113，虽然使用 JS 写的，不过 python 的实现也更新了一下

题目如下：

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Path Sum III 的解法肯定就是 I & II 的进阶版，I & II 中求的是从 root -> leaf 的和，因此好算一些，只需要遍历到 leaf，然后算一下 node.val === targetSum 就可以获取结果，不过 III 求的是任意一段和，问是不是能等同于 targetSum：

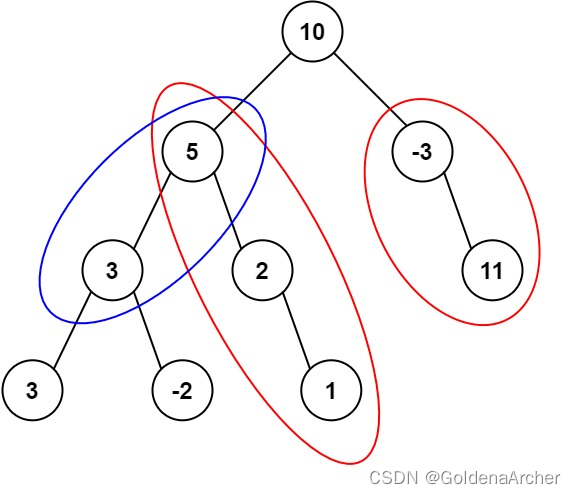
如果之前做过 leetcode 560 和为 K 的子数组, 的话，就会发现这道题就非常的熟悉， leetcode 560 和为 K 的子数组, 求的也是任意子字符串和为 k 的数量，换言之，可以理解成 437 是 leetcode 560 和为 K 的子数组, 的进阶版本，相当于结合了 leetcode 560 和为 K 的子数组, 的解法和二叉树

因此解题思路也是一样的，同样都是使用 prefix sum + hash table 去解题，这里主要需要注意一点的是，不同分支上的 dict 不能串起来，如题目中的 targetSum 是 8，那么下面这一条线路，虽然加起来的结果也是 8，但是因为在不同的树上，所以不是合法的路径：

随后套用 leetcode 560 和为 K 的子数组, 的解法使用 prefix sum 去解即可

代码如下：

class Solution:
    def pathSum(self, root: Optional[TreeNode], k: int) -> int:
        paths = 0

        def helper(root, currSum):
            if not root: return

            nonlocal paths

            currSum += root.val
            paths += m.get(currSum - k, 0)

            m[currSum] += 1
            helper(root.left, currSum)
            helper(root.right, currSum)

            m[currSum] -= 1

        paths = 0
        m = defaultdict(int)
        m[0] = 1

        helper(root, 0)

        return paths