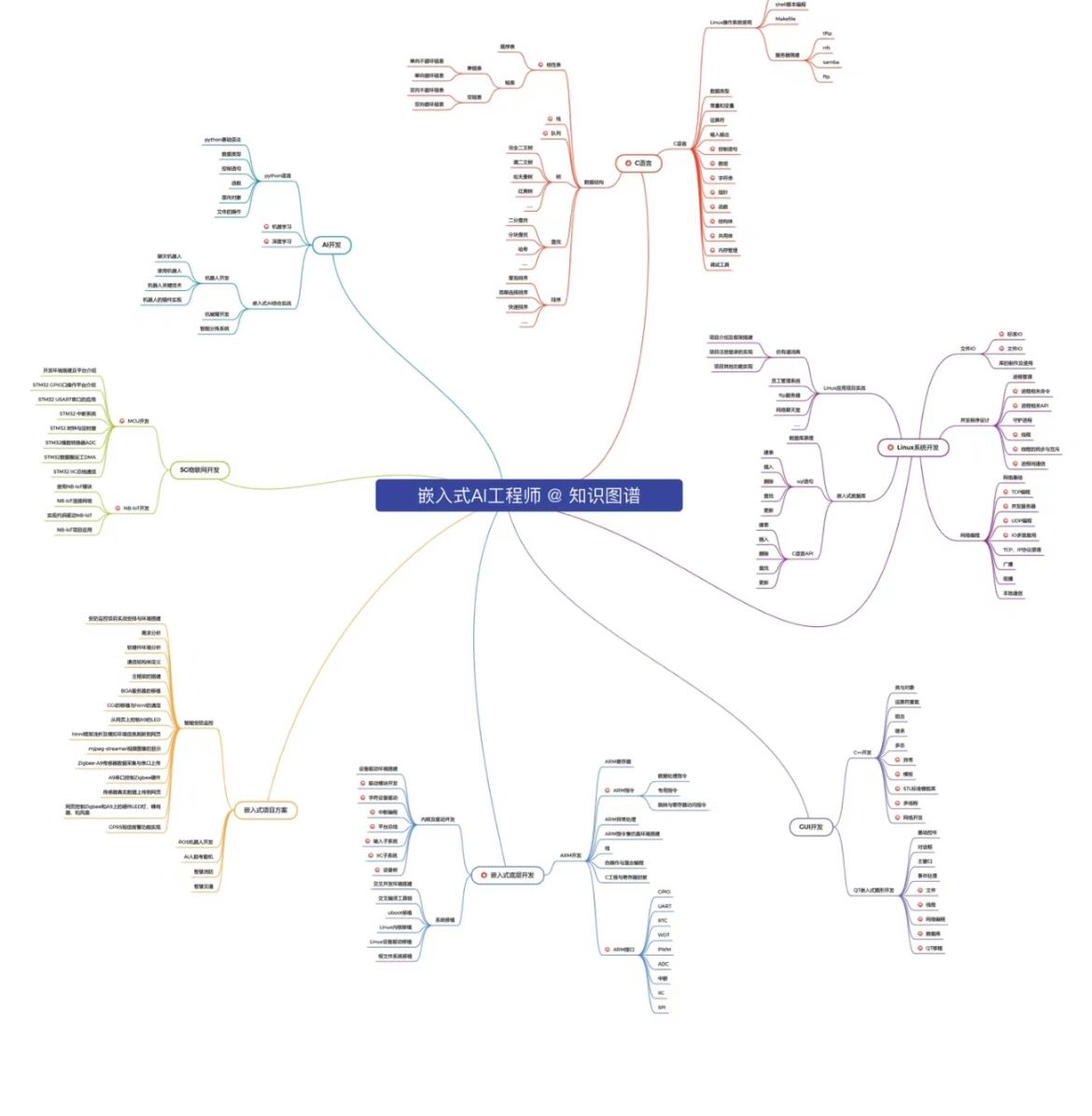
嵌入式Linux和stm32区别? 之间有什么关系吗？

主要体现在以下几个方面：

1.硬件资源不同

单片机一般是芯片内部集成flash、ram，ARM一般是CPU，配合外部的flash、ram、sd卡存储器使用。最近很多小伙伴找我，说想要一些嵌入式的资料，然后我根据自己从业十年经验，熬夜搞了几个通宵，精心整理了一份「嵌入式专业入门到高级教程+工具包」，点个关注，全部无偿共享给大家！！！

评论区回复“888”，关注我之后私信回复“666”，即可拿走。

STM32现在也出了高端的MPU，可以跑Linxu的，比如STM32MP157F。

外设方面，ARM也比单片机要多很多，也更复杂。

2.程序存储位置不同

单片机程序一般比较小，上百Kb的程序逻辑已经相对复杂的了，所以大多数产品程序一般存储在片内flash。

ARM+Linux程序比较大，还加上Linux系统，一般存在外部的存储器，如sd卡、mmc、sata等。

3.程序开发环境不同

单片机大多数是用Keil、IAR等等，开发环境比较简单。

ARM+Linxu则复杂很多，具体可以参照芯片方案。

程序的编译时间也不是一个级别的，单片机只需要几十秒，ARM+Linux，如果再跑上安卓系统，我很久以前玩过一次rk3288的，重头编译，电脑配置不错的话，大概需要几个小时。