【滑动窗口】篮里到底能装 “几个水果” 呢？

在这里插入图片描述

Problem: 904. 水果成篮

文章目录

题目分析
算法原理分析
- 暴力枚举 + 哈希表
- 滑动窗口优化
- 数组再度优化
复杂度
Code

题目分析

首先我们来分析一下本题的思路

首先我们通过题目的描述来理解一下其要表达的含义，题目给到我们一个fruit数组，里面存放的是每棵树上水果的数量。当我们拿着两个篮子去采摘水果的时候，可以选择任意一颗树开始采摘
虽然篮子里面只能装一种水果，即两个篮子只能有两种水果，但是每种水果所装的个数是不受限制的，所以只要水果的种类不超过两种即可

我们再来仔细看一下示例，比如这个示例1,{1, 2, 1}指的就是第一棵树上有一个【1号水果】，第二棵树上有一个【2号水果】，第三棵树上有一个【1号水果】。所以若是我们从第一棵开始采摘的话，可以采摘到 2个1号水果和1个2号水果
看到示例2，第一棵树上有一个【0号水果】，第二棵树上有一个【1号水果】，第三棵树上有一个【2号水果】，第三棵树上也有一个【2号水果】。
- 那若是我们从第一棵树开始采摘的话，摘完【0号】与【1号】水果就必须停下来了
- 若是我们从从第二棵树开始采摘的话，可以摘到【1号】与【2号】水果，并且【2号】水果可以采摘到两个，总水果树有3个，因此我们从第二棵树开始采摘最好
相信在看了上面的这些描述之后，读者应该是很清楚了，再来举一个例子{1, 1, 1, 1, 1, 1}，对于这个来说的话我们可以知道所摘的水果种类为1个，数量为6个

💬 那么本题我们就转换为了：找出一个最长的子数组长度，子数组中不超过两种类型的水果

算法原理分析

接下去我们就来分析一下本题的算法原理

暴力枚举 + 哈希表

首先最先相当的一定是暴力枚举，从第一个数开始往后进行枚举，以此类推，找到符合条件且长度最长的那一个。将做遍历到的加入到哈希表中，在遍历的过程中逐步进行判断即可
对于暴力解法的代码这里就不展示了，读者可以自己尝试着去写写看

滑动窗口优化

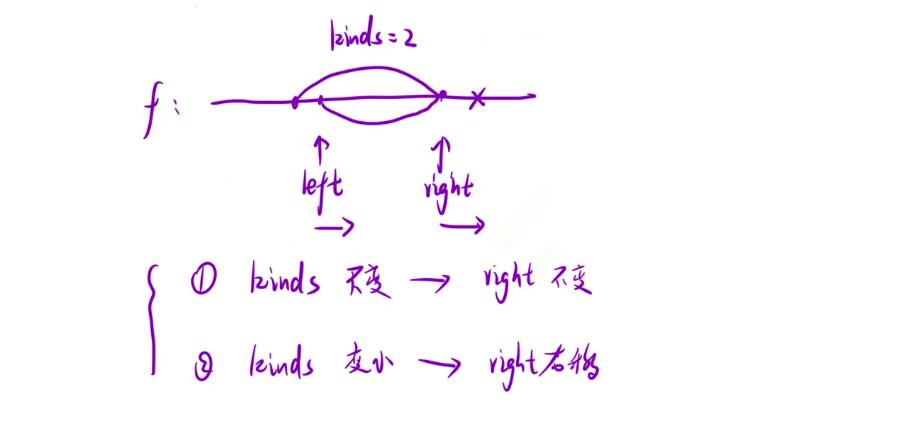
我们主要还是来讲一讲有关如何使用【滑动窗口】去做优化的事情，那对于滑动窗口而言我们知道是基于『双指针』的，所以在这里我们会需要有一个left指针和一个right指针，当这个right指针在向后移动的时候，当其无法在继续后移的时候表示[left, right]这段区间内的水果数量已经到达②了，此时我们要考虑去做【出窗口】的操作

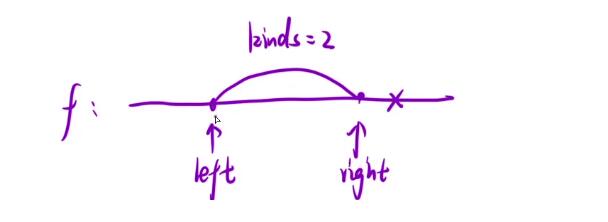
那这个时候我们让left指针向右移动一格，那此时读者可以思考一下当前的kinds会出现什么样的变化？

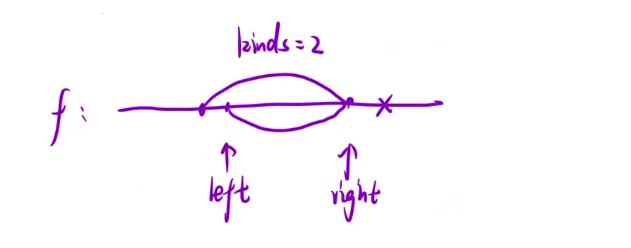
在下面我列举出了两种，一个是 kinds不变的情况，因为其在后移的过程中，所取消掉的那一个水果的种类可能在[left, right]这个区间中还存在着这个种类的水果
第二个则是 kinds变小的情况，很好理解，若是在[left, right]区间中不包含了去除掉的这种水果的话，说明种类就会减少

与之相对应的我们要给出right指针相应的变化情况，若是kinds不做变化的话，right也无需去变化，因为再去右移的话可能会增加水果的种类；若是kinds变小的话，那么right就可以右移了，此时水果的种类就可以增加上去

那接下去呢，就让我们来看看，算法的执行过程是怎样的

在这里，我们的哈希表中所存的数据种类有两个，一个是 当前的水果种类，另一个呢则是 这个水果所对应的数量。
所以当我们使用右指针right在进行遍历的时候，其所对应的个数就++，那当这个数量大于2时就开始出窗口，所对应的则是left左指针所指向的水果个数，但是呢这不是随便减的，当其减到【0】的时候，就要考虑从这个哈希表中删除掉这个相对应的水果了。
最后当出完窗口后我们要做的就是去更新这个最长的结果

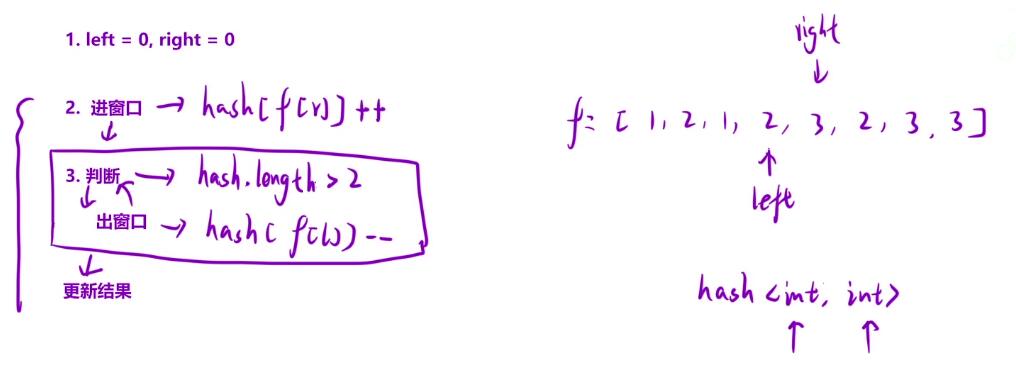
好，以上就是有关【滑动窗口】相关的算法原理分析，详情代码见【Code】

💬 那有同学问：为何不直接讲滑动窗口相关的算法呢，而是每次都要讲一下暴力的解法，这不是多此一举吗？

同学，你应该要明白，我们在笔试面试时做算法题的时候，不是一看到一道题的时候就会想到它到底需要使用什么算法与数据结构，一般在拿到一道题的时候我们一般都会先去考虑暴力的解法。在思考一段时间之后才会去思考其是都可以一些算法来进行解决，我们平常在刷题的过程中，重要的不是你马上就能想到这个算法，我们更加关注的是这个解题的过程，大家在练习算法题的时候一定要格外注意

数组再度优化

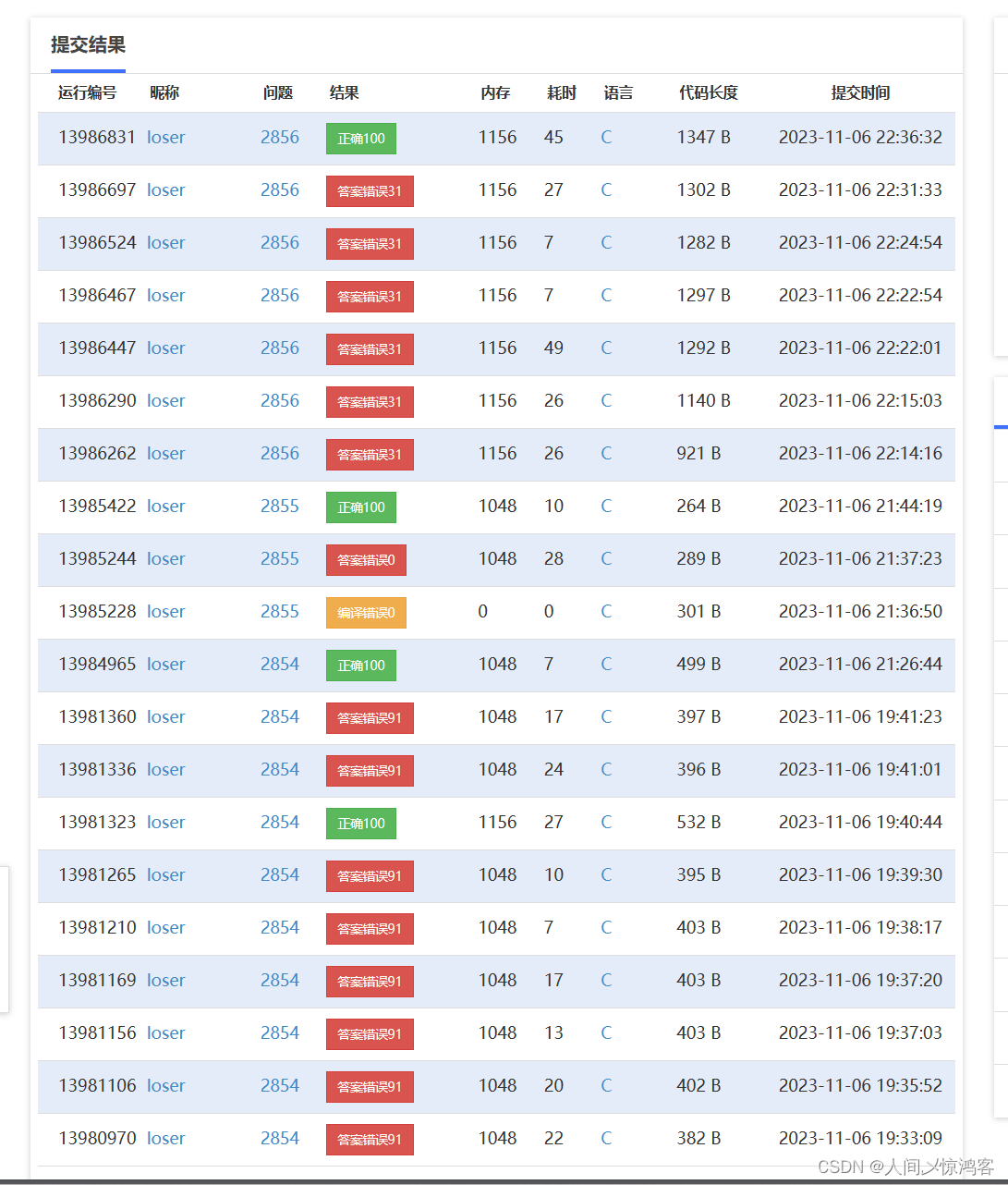
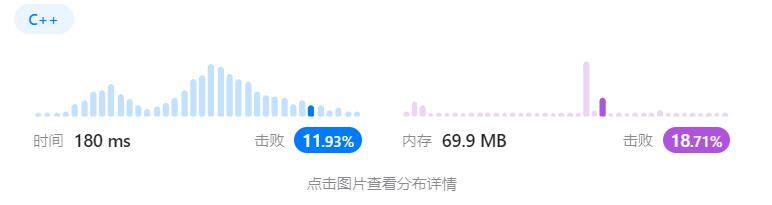
有读者一定会疑惑，已经使用【滑动窗口】去做了优化为什么还要再去优化呢？我们可以来看看滑动窗口的代码提交之后的结果

可以看到效率并不是很高，原因其实就在于我们在频繁地去出入窗口

💬 那怎么去做一个优化呢？

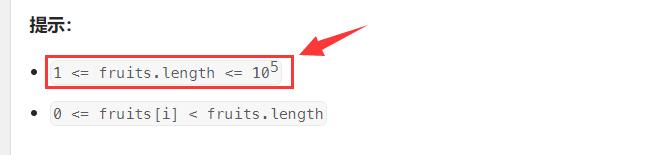
我们再来观察一下题目给到我们的提示，这个fruit数组最大的个数为 $ 10^5 $，那我们其实可以不用使用哈希表去存储，而是直接利用【数组】去进行存放，因为对于数组的每个元素来说其实就是一种映射，和哈希表其实是差不多的原理

我们可以选择直接将数组的大小定为这个大小，并且呢我们需要在循环中放一个kinds变量用于代替哈希表的个数统计

int hash[100001] = { 0 };
for(int left = 0, right = 0, kinds = 0; right < n; ++right)

那么当我们在碰到水果的个数减到0的时候，不去使用erase，而是直接kinds--去控制当前窗口中的水果个数

if(hash[fruits[left]] == 0)
    // hash.erase(fruits[left]);
    kinds--;

那么当我们一进循环遍历的时候，也需要去做一个判断，若是当前遍历到的这个水果的个数为0的话，就将kinds的个数进行一个累加

// 一进来判断发现水果的种类为0的话，则水果种类增加一种
if(hash[fruits[right]] == 0)  
    kinds++;

那么在最后当我们中途去判断这个水果个数的时候，只需要对这个kinds做出判断即可

fi(kinds > 2)

💬 具体代码可以参照【Code】部分，我们来看到提交之后的执行结果可以观察到性能确实得到了大幅度的提升

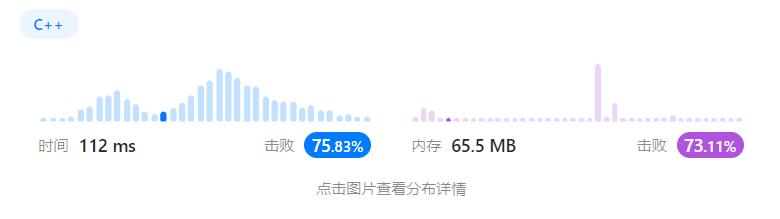
复杂度

接下去我们来分析一下时间复杂度

时间复杂度:

首先是对于时间复杂度而言,【滑动窗口】部分的代码, 我们使用left和right双指针去遍历查找整个数组, 并且在查找的过程中遇到水果数量 > 2需要去做出窗口的操作，因为erase()的复杂度为 $O (n)$ , 所以在最坏的情况下复杂度可以到达 $O(n^2)$

而对于数组优化来说, 虽免去了哈希表，没了计数的功效。但是我们只是去做了遍历的操作，中间循环的过程使用的是kinds作的标记操作，不涉及erase()，因此最坏的复杂度因为 $O (n)$

空间复杂度:

对于空间复杂度来说，两种优化的方法并没有涉及额外空间的申请, 所以空间复杂度即为： $O (1)$

Code

接下去是代码部分

首先的话是有关【滑动窗口】优化的代码


  class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        unordered_map<int, int>hash;

        int max_len = INT_MIN;
        for(int left = 0, right = 0; right < n; ++right)
        {
            // 1.进窗口
            hash[fruits[right]]++;
            // 当水果的种类多于2种的时候，开始出窗口
            if(hash.size() > 2)
            {
                // 2.出窗口【此时left不能后移，因此要删除该水果】
                hash[fruits[left]]--;
                // 如果当前水果种类的数量到0的话，将其从哈希表中删除
                if(hash[fruits[left]] == 0)
                    hash.erase(fruits[left]);
                left++;
            }
            // 更新结果
            max_len = max(max_len, right - left + 1);
        }
        return max_len == INT_MIN ? 0 : max_len;
    }
};

然后的话是有关【数组优化】的代码

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int n = fruits.size();
        //unordered_map<int, int> hash;
        int hash[100001] = { 0 };
        int max_len = INT_MIN;
        for(int left = 0, right = 0, kinds = 0; right < n; ++right)
        {
            // 一进来判断发现水果的种类为0的话，则水果种类增加一种
            if(hash[fruits[right]] == 0)  
                kinds++;
            // 1.进窗口
            hash[fruits[right]]++;
            // 判断当前哈希表中水果的种类是否超过两种
            if(kinds > 2)
            {
                // 2.出窗口
                hash[fruits[left]]--;
                // 如果在出窗口之后当前水果的数量为0的话，则从哈希表中删除该水果
                if(hash[fruits[left]] == 0)
                    // hash.erase(fruits[left]);
                    kinds--;
                left++;
            }
            // 3.更新最大长度
            max_len = max(max_len, right - left + 1);
        }
        return max_len == INT_MIN ? 0 : max_len;
    }
};