---

文章目录

• 格子游戏
• 搭配购买
• 程序自动分析
• 奇偶游戏
• 银河英雄传说

---

一、格子游戏OJ链接

        本题思路:本题首先我们将题目中所给的二维坐标映射到一维坐标中，从坐标从0开始进行，而题目中是从1开始，我们需要先进行--操作，然后利用并查集来判断即可。

#include <bits/stdc++.h>

constexpr int N=40010;

int n,m;
int p[N];

int find(int x)
{
	if(x!=p[x]) p[x]=find(p[x]);
	return p[x];
}

int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);

	std::cin>>n>>m;

	for(int i=0;i<n*n;i++) p[i]=i;//并查集的初始化操作

	int res=0;
	for(int i=1;i<=m;i++){
		int x,y;
		char op;

		std::cin>>x>>y>>op;
		x--,y--;
		int a=x*n+y;//这里我们需要将二维坐标转换成一维坐标
		int b;
		if(op=='D') b=(x+1)*n+y;
		else b=x*n+y+1;

		int pa=find(a),pb=find(b);
		if(pa==pb)
		{
			res=i;
			break;
		}
		p[pa]=pb;
	}
	
	if(res==0) std::cout<<"draw"<<std::endl;
	else std::cout<<res<<std::endl;
	return 0;
}

二、搭配购买OJ链接

        本题思路:本题每行两个整数 ui，vi，表示买 ui就必须买 vi，同理，如果买 vi 就必须买 ui。这里就可以通过并查集的方式将两个整数合并到一个集合里面看成一个物品的方式，然后在有限的w的价格下买最大价值的商品这可以利用01背包问题求解。

#include <bits/stdc++.h>

constexpr int N=1e5+10;

int n,m,w;
int c[N],d[N];
int p[N];
int f[N];

int find(int x)
{
	if(x!=p[x]) p[x]=find(p[x]);
	return p[x];
}

void merge(int a,int b)//这里合并的时候需要将此时的集合内的所有元素看成一个就需要将价值和价钱合并
{
	int pa=find(a),pb=find(b);
	if(pa!=pb){
		p[pa]=pb;
		c[pb]+=c[pa];
		d[pb]+=d[pa];
	}
}

int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);

	std::cin>>n>>m>>w;

	for(int i=1;i<=n;i++) p[i]=i;//并查集初始化动作
	for(int i=1;i<=n;i++) std::cin>>c[i]>>d[i];


	while(m--){
		int a,b;
		std::cin>>a>>b;
		merge(a,b);//合并操作
	}

	for(int i=1;i<=n;i++){//进行01背包处理
		if(i==p[i]){
			for(int j=w;j>=c[i];j--)
				f[j]=std::max(f[j],f[j-c[i]]+d[i]);
		}
	}

	std::cout<<f[w]<<std::endl;
	return 0;
}

三、程序自动分析OJ链接

        本题思路:由于数据范围是1e9次方，题中所给的变量范围1e5方，但是我们只需要合并2e5个这里我们就可以使用离散化解决问题。我们定义一个query来保存每一个问题方便我们最后一次扫描找出答案。如果i==j我们可以使用并查集解决问题。

#include <bits/stdc++.h>

constexpr int N=2e5+10;//由于题目中所给的数据范围为1e9所以我们需要进行离散化处理只需要合并2e5个

int n;
std::unordered_map<int,int> hash;//利用哈希来映射
int idx;

struct Query//表示操作关系
{
	int a,b,op;
}q[N];

int p[N];

int s(int x)//这里就是下标映射
{
	if(hash.count(x)) return hash[x];
	return hash[x]=++idx;
}

int find(int x)
{
	if(p[x]!=x) p[x]=find(p[x]);
	return p[x];
}

int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);

	int T;
	std::cin>>T;
	while(T--){
		idx=0;
		hash.clear();

		for(int i=1;i<=N;i++) p[i]=i;

		std::cin>>n;
		for(int i=1;i<=n;i++){
			int a,b,e;
			std::cin>>a>>b>>e;
			//首先进行离散化处理
			a=s(a),b=s(b);
			q[i]={a,b,e};
			if(e) //如果是1表示a和b相等此时需要进行合并
				p[find(a)]=find(b);
		}

		bool flag=true;
		for(int i=1;i<=n;i++){//扫描一遍
			if(!q[i].op){
				int a=q[i].a,b=q[i].b;
				if(find(a)==find(b)){
					flag=false;
					break;
				}
			}
		}

		if(flag) std::cout<<"YES"<<std::endl;
		else std::cout<<"NO"<<std::endl;
	}
	return 0;
}

四、奇偶游戏OJ链接

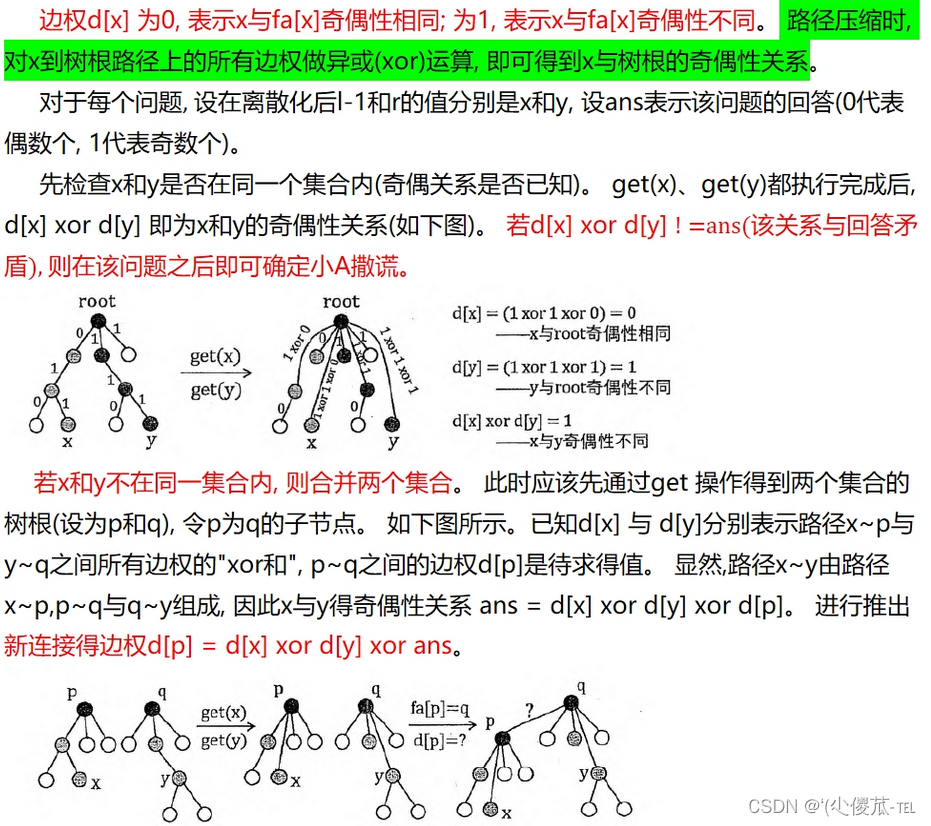
        本题思路:本题可以首先采用前缀和的思想，用sum数组表示序列S的前缀和，分为两种情况:第一种情况就是如果S[L~R]有偶数个1，则sum[L-1]和sum[R]奇偶性相同，第二种就是如果S[L~R]有奇数个1，则sum[L-1]和sum[R]奇偶性不同。由于本题序列长度很大而问题较少所以我们需要进行离散化处理。本题是多种传递关系，首先我们采用边带权的并查集解决。或者是采用扩展域并查集的方式解决。摘要这位大佬

#include <bits/stdc++.h>

constexpr int N=2e4+10;

int n,m;
int p[N],d[N];
std::unordered_map<int,int> hash;
int idx;

int s(int x)
{
	if(hash.count(x)) return hash[x];
	return hash[x]=++idx;
}

int find(int x)
{
	if(x!=p[x]){
		int root=find(p[x]);
		d[x]^=d[p[x]];
		p[x]=root;
	}
	return p[x];
}

int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);

	std::cin>>n>>m;

	for(int i=1;i<=N;i++) p[i]=i;

	int res=m;//如果没有矛盾则答案为所给的问题数量
	for(int i=1;i<=m;i++){
		int a,b;
		std::string type;
		std::cin>>a>>b>>type;
		a=s(a-1),b=s(b);//对s[a-1],s[b]进行离散化处理

		int t=0;//0表示该问题时奇数1表示偶数
		if(type=="odd") t=1;

		int pa=find(a),pb=find(b);
		if(pa!=pb)//如果离散化之后的a,b不在同一个集合则需要进行合并集合
		{
			p[pa]=pb;
			d[pa]=d[a]^d[b]^t;
		}
		else{
			if((d[a]^d[b])!=t){
				res=i-1;
				break;
			}
		}
	}

	std::cout<<res<<std::endl;
	return 0;
}

         

#include <bits/stdc++.h>

constexpr int N=2e4+10;
constexpr int Base=N/2;

int n,m;
int p[N],d[N];
std::unordered_map<int,int> hash;
int idx;

int s(int x)
{
	if(hash.count(x)) return hash[x];
	return hash[x]=++idx;
}

int find(int x)
{
	if(x!=p[x])p[x]=find(p[x]);
	return p[x];
}

int main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);

	std::cin>>n>>m;

	for(int i=1;i<=N;i++) p[i]=i;

	int res=m;//如果没有矛盾则答案为所给的问题数量
	for(int i=1;i<=m;i++){
		int a,b;
		std::string type;
		std::cin>>a>>b>>type;
		a=s(a-1),b=s(b);//对s[a-1],s[b]进行离散化处理

		if(type=="even"){
			if(find(a+Base)==find(b)){
				res=i-1;
				break;
			}
			p[find(a)]=find(b);
			p[find(a+Base)]=find(b+Base);
		}
		else{
			if(find(a)==find(b)){
				res=i-1;
				break;
			}
			p[find(a+Base)]=find(b);
			p[find(a)]=find(b+Base);
		}
	}

	std::cout<<res<<std::endl;
	return 0;
}

五、银河英雄传说OJ链接

         本题思路:本题可以采用并查集,size[x]表示集合的大小，dist[x]表示x到p[x]的距离。将第a列的船接在第b列的末尾,相当于让每个点到pb的距离都加上size[pb]，由于存储并查集中存在路径压缩的效果，因此只需要将pa到pb的距离加上size[pb]即可，即d[pa] = size[pb]，其他跟着pa后面的元素的路径进行压缩且更新dist[i]的值。路径压缩首先找到根结点root,计算父节点到上一个父节点的距离dist[p[x]],同时进行路径压缩(路径压缩后，上一父节点即root),dist[x]初始值是x到p[x]的距离，更新dist[x]值，即dist[x] = dist[x] + dist[p[x]]。

#include <bits/stdc++.h>

constexpr int N=30010;

int p[N];
int size[N];//表示当前列包含的所有元素的个数
int dist[N];//表示某个元素到根的距离

int find(int x)
{
    if(p[x]!=x){
        int root=find(p[x]);
        dist[x]+=dist[p[x]];
        p[x]=root;
    }
    return p[x];
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);std::cout.tie(nullptr);

    int T;
    std::cin>>T;

    for(int i=1;i<=N;i++){
        p[i]=i;
        size[i]=1;
    }

    while(T--){
        char op;
        int a,b;
        std::cin>>op>>a>>b;

        int pa=find(a),pb=find(b);
        if(op=='M'){
            if(pa!=pb){
                dist[pa]=size[pb];
                size[pb]+=size[pa];
                p[pa]=pb;
            }
        }
        else{
            if(pa!=pb) std::cout<<-1<<std::endl;
            else std::cout<<std::max(0,std::abs(dist[a]-dist[b])-1)<<std::endl;
        }
    }
    return 0;
}