8.1 如何理解逻辑回归
逻辑回归根据给定的自变量数据集来估计事件的发生概率,由于结果是一个概率,因此因变量的范围在 0 和 1 之间。
逻辑回归的与线性回归一样,也是以线性函数为基础的;而与线性回归不同的是,逻辑回归在线性函数的基础上添加了一个非线性函数,如sigmoid函数,使其可以进行分类。
逻辑回归是一种典型的分类问题处理算法,其中二分类(LR)是多分类 (softmax)的基础或者说多分类可以由多个二分类模拟得到。
8.2 逻辑回归算法实现过程
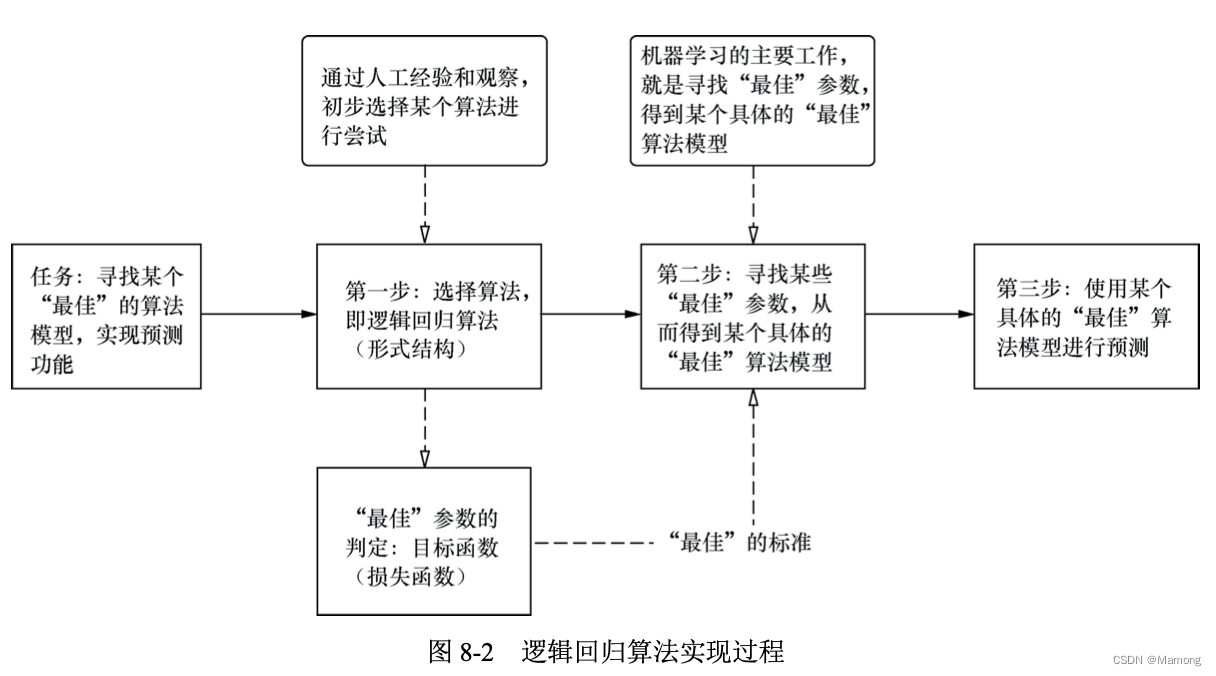
(1)选择算法。
根据经验和观察,我们认为房屋面积、房间数、朝向、地址等特征变量与目标变量“房价” 之间似乎存在着某种线性关系,应该用线性回归算法来表达。但是,现在情况有了变化,历史样本数据中的“房价”数据只给出“高档房屋”“普通房屋”这种分类,因此需要将线性回归算法的函数值压缩为 0 ~ 1。
sigmoid 函数恰好提供了这样的功能。将线性回归算法的函数值 f (x) 作为 sigmoid 函数的自 变量,就可以得到![]() ,从而将最终“房价”计算值压缩为 (0,1)。
,从而将最终“房价”计算值压缩为 (0,1)。
(2)损失函数。
在线性回归模型中,我们采用最小二乘法,也就是均方误差作为“差别” 的度量标准,所以我们需要找到一组参数 w 和 b,使得均方误差最小化。但是逻辑回归模型表达式是非线性的,这会造成均方误差表达式不是凸函数,无法采用常用的梯度下降法来求解使得损失函数最小化的参数值。研究者们最后提出了如下的损失函数:
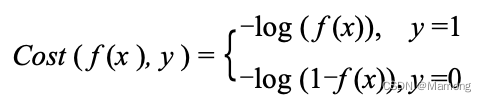
第一,我们寻找的损失函数一定符合这样的特点:如果真实值和计算值差距很大,那么损失函数的值一定很大;如果真实值和计算值差距很小,那么损失函数的值一 定很小。
第二,这里的 y 表示房价档次的真实值,可能是 0 或者 1;这里的 f (x) 表示的是把一组特 征变量的历史数据(房屋面积、房间数等)作为自变量输入具体逻辑回归模型(带有参数)后 计算出来的数值,这个结果是 (0,1) 的某个实数。
第三,当真实值是“高档房屋”,也就是 y =1 所表达的含义。如果某组参数确定的逻辑回 归模型f (x)计算出的房价档次数值越接近1,就说明这是一组不错的参数,那么损失函数值就应该越小。当 f (x)趋近1时,损失函数表达式-log( f (x))的数值趋近0,非常符合要求。如果f (x)趋近0,损失函数趋于+∞,说明这组参数非常糟糕。
第四,当真实值是“普通房屋”,也就是 y = 0 所表达的含义。f(x)和损失函数趋势类似三。
(3)参数估计。
上述损失函数本质上也是一个凸函数。而对凸函数就可以采用梯度下降法来求解损失函数值达到最小时所对应的参数值。具体做法与线性回归算法类似。
(4)正则化。
为了解决这种过拟合的问题,也需要采取正则化的方法,将系数估计朝 0 的方向进 行约束、调整或缩小,降低模型在学习过程中的复杂度和不稳定程度,从而尽量避免过拟合情况。