1、Kittler算法（最小误差法）概述

最小误差法是 J. Kittler & J. Illingworth 1986年在《MINIMUM ERROR THRESHOLDING》文章中提出的一种基于直方图的阈值分割方法,简称 Kittler 算法。其思想:假设灰度图像由目标和背景组成,且目标和背景满足一混合高斯分布,计算目标和背景的均值、方差,根据最小分类误差思想得到的最小误差目标函数,取目标函数最小时的阈值即为最佳阈值。按此阈值将图像分割为二值图像。

Kittler算法与Otsu方法效果接近，但速度更快，更适宜应用于像素质量较高的图像中。
Kittler算法的中心思想是，计算整幅图像的梯度灰度的平均值，以此平均值做为阈值。
 

2、Kittler算法源代码

using System;
using System.Linq;
using System.Text;
using System.Drawing;
using System.Collections;
using System.Collections.Generic;
using System.Runtime.InteropServices;
using System.Drawing.Imaging;

namespace Legalsoft.Truffer.ImageTools
{
    public static partial class BinarizationHelper
    {
        #region 灰度图像二值化 全局算法 Kittler 算法

        /// <summary>
        /// Kittler算法
        /// </summary>
        /// <param name="data"></param>
        public static void Kittler_Algorithm(byte[,] data)
        {
            int height = data.GetLength(0);
            int width = data.GetLength(1);
            double sumGrads = 0.0;
            double sumGrayGrads = 0.0;
            for (int y = 1; y < height - 1; y++)
            {
                for (int x = 1; x < width - 1; x++)
                {
                    double Grads = Math.Max(Math.Abs(data[y - 1, x] - data[y + 1, x]), Math.Abs(data[y, x - 1] - data[y, x + 1]));
                    sumGrads += Grads;
                    sumGrayGrads += Grads * (data[y, x]);
                }
            }
            int threshold = (int)(sumGrayGrads / sumGrads);
            Threshold_Algorithm(data, threshold);
        }

        #endregion
    }
}

The Kittler binarization method is a classic binarization method based on histogram. ... The idea is: first cut the image into small patches of the same size, and then use the method mentioned in the paper to calculate a local (relative to the entire image) threshold for each small patch, and then use bilateral interpolation 

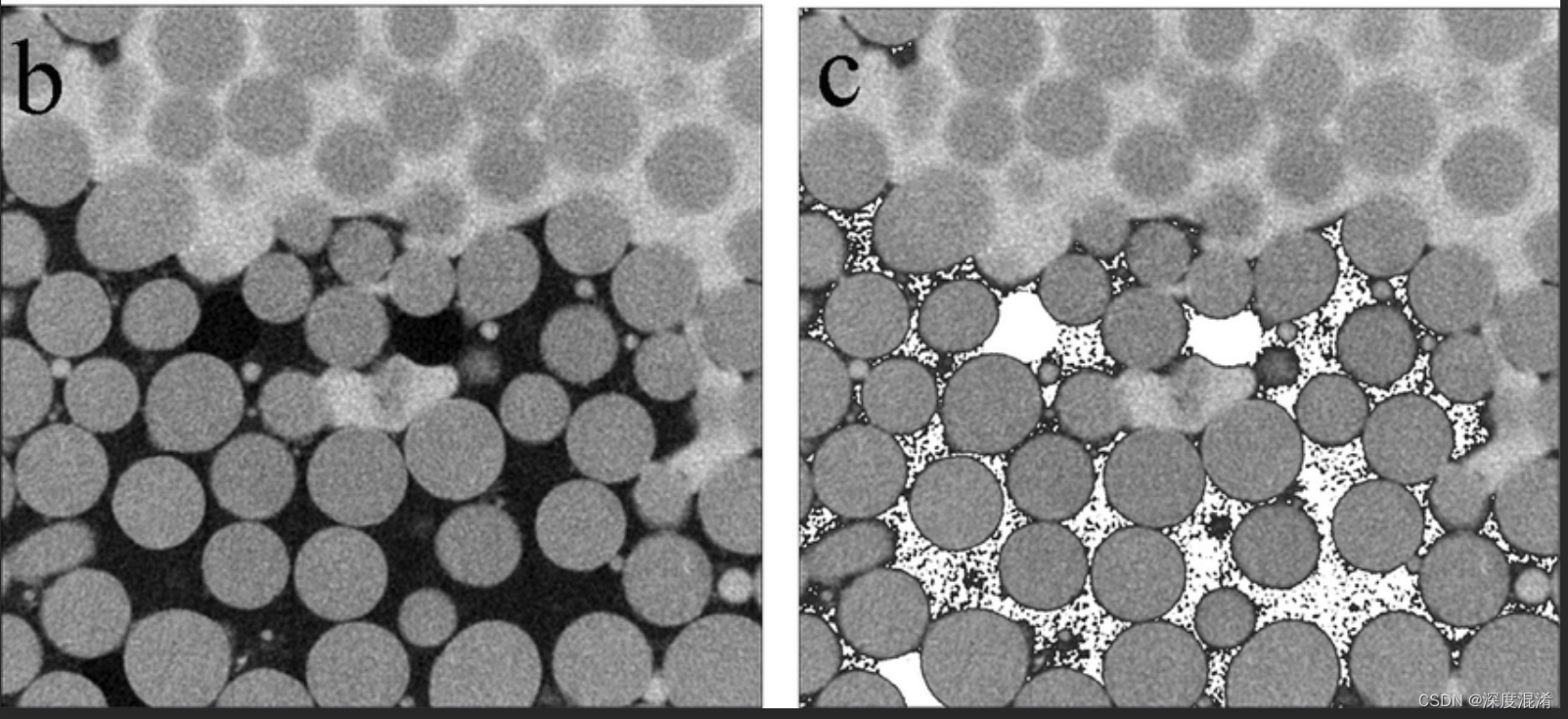
3、Kittler算法的二值化效果以及与基本阈值算法的对比

 The Kittler binarization method is a classic binarization method based on histogram. Proposed by J. Kittler in the paper " Minimum Error Thresholding" published in 1986 .