目录
- 学习目的
- 软件版本
- 原始文档
- 一元线性回归分析
- 一、实战案例
- 二、统计策略
- 三、SPSS操作
- 四、结果解读
- 第一个表格为模型摘要
- 第二表格为方差分析表
- 第三个表格为模型系数
- 第四张散点图(主要检验方差齐性)
- 第五张直方图和P-P图(检验残差正态性)
- 五、规范表达
- 1、规范表格
- 2、规范文字
- 六、划重点
学习目的
SPSS第二十讲: 一元线性回归分析怎么做?
软件版本
IBM SPSS Statistics 26。
原始文档
《小白爱上SPSS》课程
#统计原理
一元线性回归分析
一元线性回归是指分析两个变量间(自变量x和因变量y)数量依存关系和影响的统计分析方法。
对于只涉及一个自变量的一元线性回归模型可表示为:
y= b0+b1 X+ϵ
Y:回归模型中的因变量,即样本的预测值。
X:回归模型中的自变量,即样本的特征数值。
ε:回归模型中的误差项,即不能被x与y之间线性关系解释的变异性。
b0:是常量。
b1: 回归系数。
一、实战案例
小白想了解下大侠的人均月收入能否预测他们年体育消费额,试构建一元线性回归模型,并检验其显著性。
读数据:
GET
FILE='E:\E盘备份\recent\小白爱上SPSS\小白数据\第二十讲:一元线性回归分析.sav'.
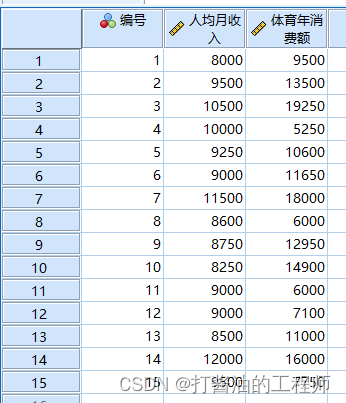
该案例主要研究人均月收入与体育消费额的关系,从专业知识上可认为人均月收入是可以预测他们的年体育消费额。
二、统计策略
针对上述案例,扪心六问。
Q1:本案例研究目的是什么?
A:关联研究,在理论上认为变量之间存在因果关系,即月收入可预测体育消费额。
Q2:本案例属于什么研究设计?
A:调查性研究。
Q3:分析数据有多少组?
A:两组数据。
Q4:有几个变量?
A:有两个变量,两变量均为连续性变量
自变量为人均月收入
因变量为体育年消费额。
Q5:变量之间是否相关?
A:变量之间需要满足线性相关,呈现线性趋势。
Q6:残差是否具有独立性、方差齐性和正态分布?
A:需要检验残差是否满足独立性、方差齐性和正态性
概括而言,如果数据满足以下条件,则可适用一元线性回归分析。
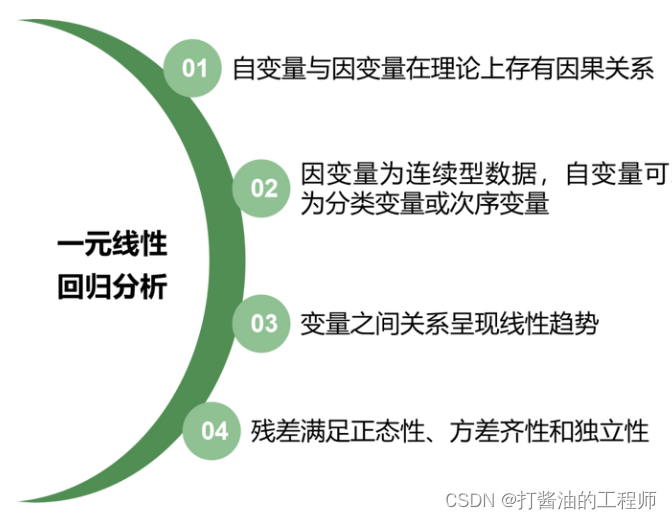
三、SPSS操作
Step1:根据散点图初步判断数据的趋势:依次点击“图形——旧对话框——散点图/点图”。
Step2: 在弹出的对话框中选择“简单散点图”,点击“定义”。将“体育年消费额”放进Y轴中,并将“人均月收入”放进X轴中,并添加标题“人均月收入与体育年消费额的关系”。
命令行:
GRAPH
/SCATTERPLOT(BIVAR)=人均月收入 WITH 体育年消费额 /*X轴 WITH Y轴*/
/MISSING=LISTWISE
/TITLE='人均月收入与体育年消费额的关系'.
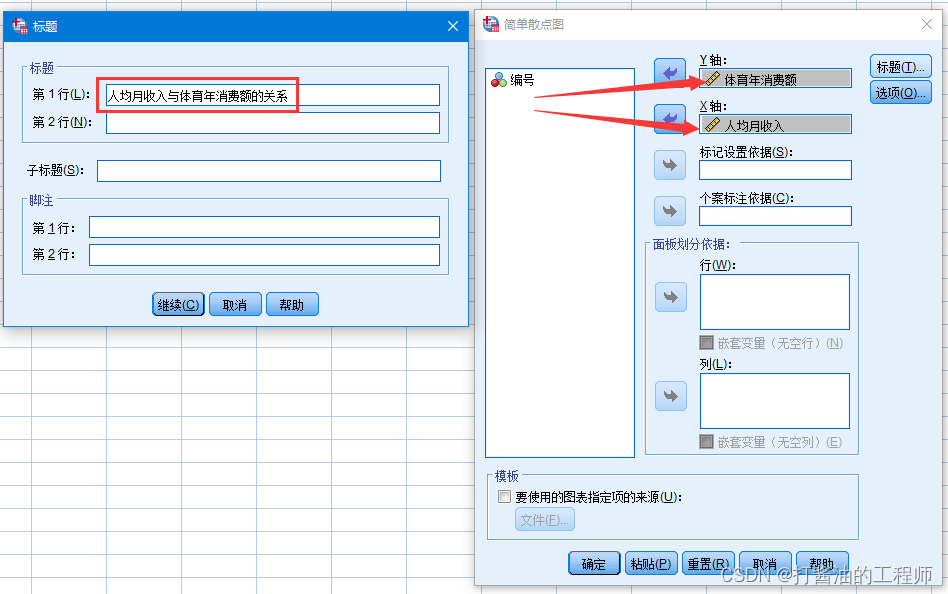
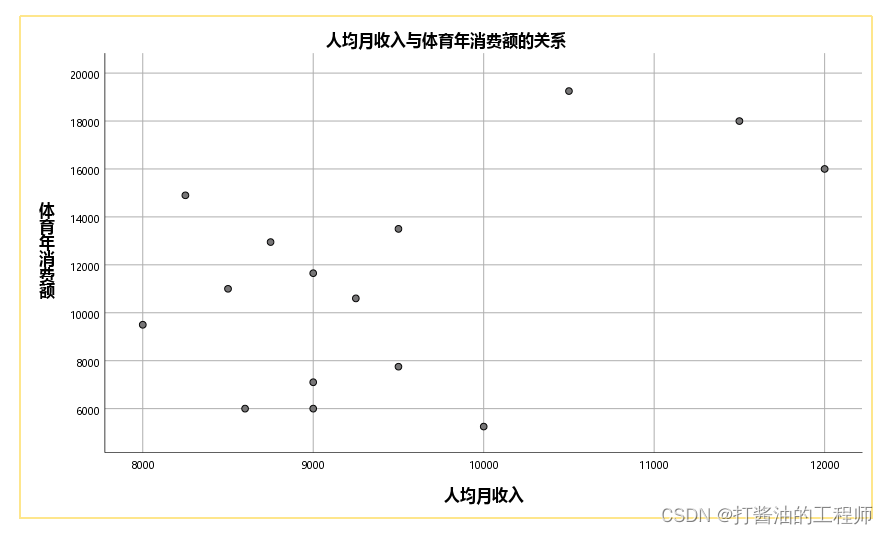
根据散点图可得出,人均月收入和他们的年体育消费额存在较为正相关关系,适合建立一元线性回归模型。
Step3:依次点击“分析——回归——线性”
Step4:在弹出“线性回归”对话框中,将“年体育消费额”放入因变量框中,将“人均月收入”变量放入自变量框中,方法默认选择“输入”。
Step5:然后单击线性回归右侧的“统计”,在弹出的选项对话框中勾选“估算值”、“模型拟合”、“描述”和“德宾-沃森,单击“继续”。
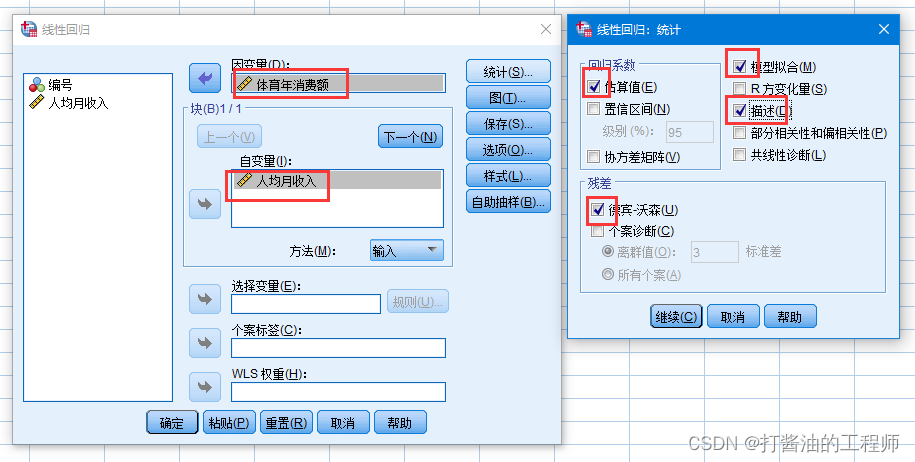
Step6:在弹出“线性回归:图”对话框中将 “*ZRESID”(标准化残差)放入Y轴中,将“*ZPRED”(标准化预测值)放入X轴中,勾选“直方图”和“正态概率图”,单击“继续”。点击“确定”。
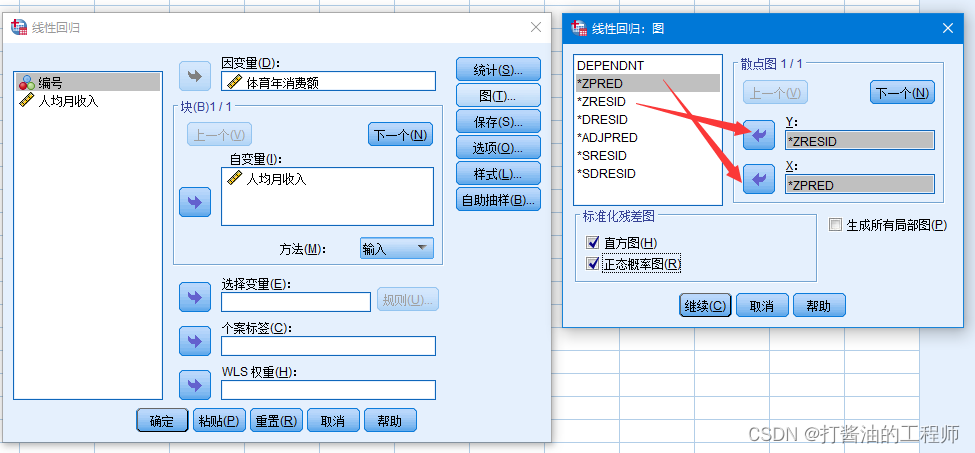
命令行:
REGRESSION
/DESCRIPTIVES MEAN STDDEV CORR SIG N
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT 体育年消费额
/METHOD=ENTER 人均月收入
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS DURBIN HISTOGRAM(ZRESID) NORMPROB(ZRESID) /*德宾残差(默认值),直方图、正态概率图*/.
四、结果解读
测量的结果有多个表格,在此讲解几个重点表格。
第一个表格为模型摘要
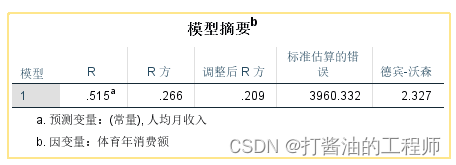
a. 预测变量:(常量), 人均月收入
b. 因变量:体育年消费额
①R是回归的多重相关系数。当简单线性回归中只有一个自变量时,R值与因变量和自变量的皮尔逊相关系数相同,代表两者之间的相关程度。如该研究中R=0.515,提示月收入与体育消费额存在中等相关。但实际上,简单线性回归并不关注R值。
②***R2(R Square)***代表回归模型中自变量对因变量变异的解释程度,是分析回归结果的开始。本研究中,R2=0.266,提示自变量(月收入)可以解释26.6%的因变量(体育消费额)变异。但是,R2是会夸大自变量对因变量变异的解释程度,如果模型中增加一个自变量,即使这个自变量在统计上并不显著,R2也会增大。
③调整 R2,是指剔除了自变量个数的影响,这使得调整R2永远小于R2,且调整R2的值不会由于自变量个数的增加而越来越接近1。本研究中,调整 R2=0.209,小于R2=0.266,校正了R2对于总体自变量对因变量变异解释程度的夸大作用。所以,当多个自变量,一般报告调整R2。
④德宾-沃森(D-W)检验,一般检验值分布在0-4之间,越接近2,观测值相互独立的可能性越大。本例子中D-W=2.327,可以认为符合线性回归独立性的条件。
第二表格为方差分析表
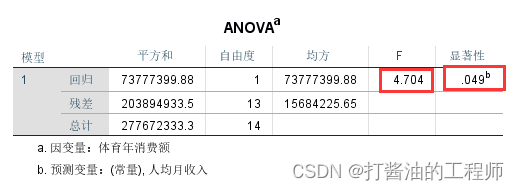
a. 因变量:体育年消费额
b.预测变量:(常量), 人均月收入
由表中可知,F=4.704,P=0.049<0.05,具有统计意义,不支持原假设,即回归方程的线性关系显著。表明人均月收入是影响体育年消费额的显著性因素。
第三个表格为模型系数
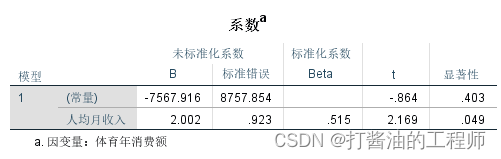
a. 因变量:体育年消费额
①是回归系数b值,本例中常数和人均月收入的系数分别为-7567.916和2.002。可得出一元线性回归模型:y ̌=-7567.916+2.002×人均月收入
②是回归系数的抽样误差,即标准误。
③Beta值(β值),是标准化b值,标准化回归系数。可以用来比较各个自变量x对y的影响程度的。本例的标准化回归方程:y=0.515×人均月收入。
④t值,是各个回归系数进行假设检验的检验统计量,线性回归检验统计量为t值。
⑤显著性:即P值。P<0.05说明自变量与因变量回归关系成立,有关系,有影响。本例中回归系数达到显著水平(P<0.05),t=2.169, p=0.049。
上面一行是常量的t和p值,一般不用关注。
第四张散点图(主要检验方差齐性)
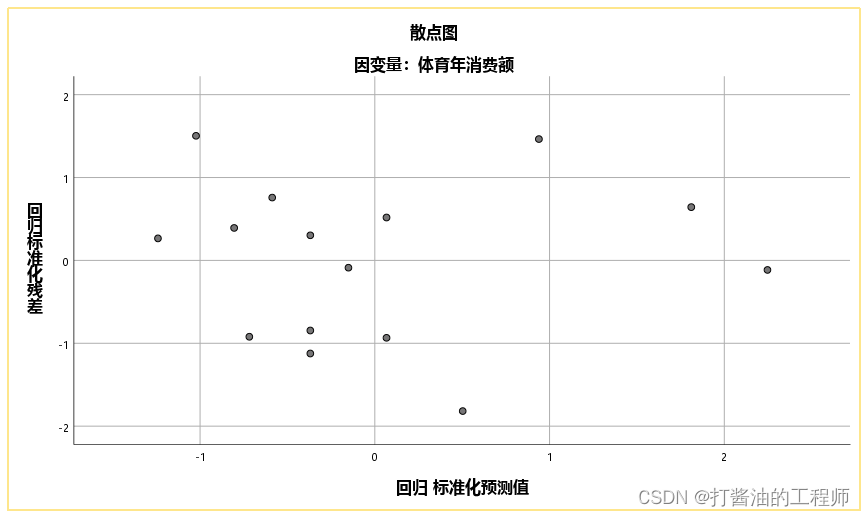
如果方差齐,不同预测值对应的残差应大致相同。即图中各点均匀分布,无特殊的分布形状。如果残差点分布不均匀,形成漏斗或者扇形,那么就方差不齐(如下图)。
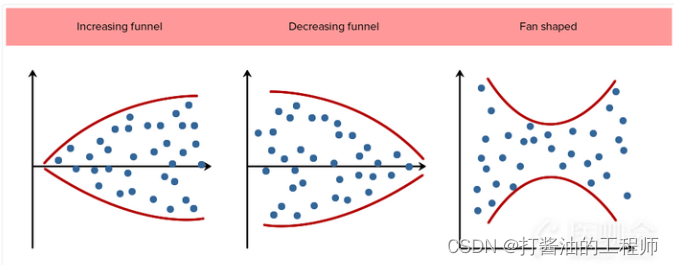
本研究结果显示,标准化残差与标准化预测值的散点图中各点均匀分布,虽然在头部相对集中,但不是十分严重,因此认为满足方差齐。
当然,如果不满足方差齐性假设,我们也可以通过一些统计手段进行矫正。比如,采用加权最小二乘法回归方程,改用更加稳健的分析方法以及转换数据等。
第五张直方图和P-P图(检验残差正态性)
(1)标准化残差的直方图
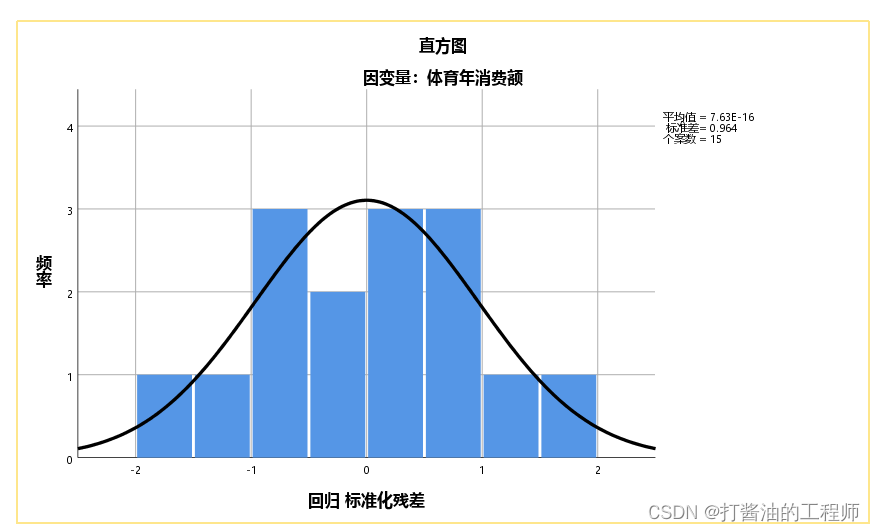
从图中可以看出,标准化残差近似正态分布。
(2)残差的P-P图
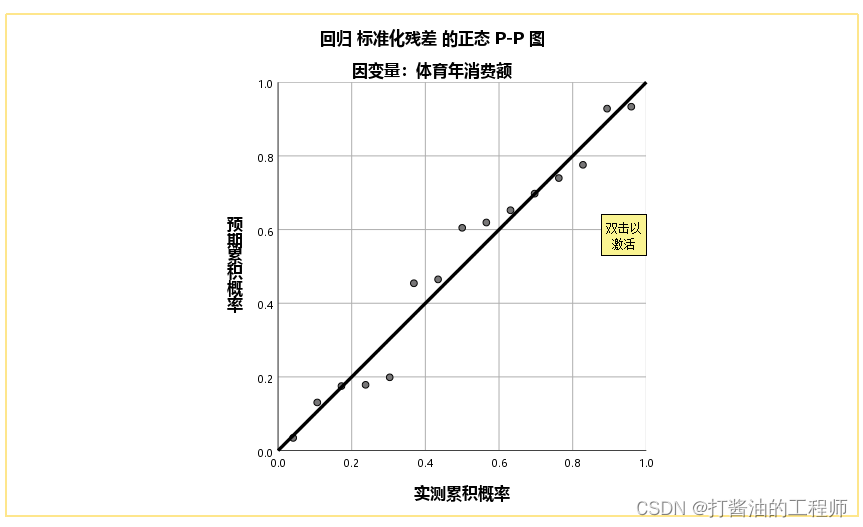
P-P图各点分布离对角线越近,提示数据越接近于正态分布;如果各点刚好落在对角线上,那么数据就是正态分布。简单线性回归仅要求回归残差接近于正态分布,因此根据上图,我们认为该数据满足近似正态性。
综上检验可知,本案例的数据满足独立性、方差齐性和正态性三个条件。
五、规范表达
规范报告有多种方式,本公众号只提供一种方式供参考。
1、规范表格

2、规范文字
采用线性回归分析结果显示,人均月收入可显著预测体育消费额,β=0.515,t=2.169, p=0.049。人均月收入可解释体育消费额的26.6%的方差。
六、划重点
1、回归分析本质上是探讨变量之间相关关系,只有在理论上满足自变量与因变量之间存在因果关系,才可开展回归分析。此外,即使回归分析显著,在解释因果关系也需谨慎。
2、一元线性回归分析需要满足变量之间存在线性关系,如果不是,则不能采用线性回归分析,这可通过散点图来判断线性关系。
3、回归分析还需满足独立性、方差齐性和正态性。独立性采用德宾-沃森(D-W)残差相关性检验;方差齐性采用残差散点图来检验;正态性采用残差正态分布图和P-P图来判断。
4、如果回归分析只是建立自变量与因变量之间关系,无须根据自变量预测因变量的容许区间和可信度等,则方差齐性和正态性可以适当放宽。
5、回归分析一般要报告回归系数(b或β值)以及显著性(P值)、R2(或调整R2)和回归模型的方差分析结果(F值和P值)。