一，前缀函数
1，定义
该函数存储一个字符串的各个长度的子串真前缀与真后缀相等的长度（注意，真前缀最多长度为n-1，不包含最后一个字符，真后缀同理，不包含第一个字符）
用p[i]数组储存值，i表示字符串下标
eg;abcabc的p[0](a)=0,p[1](ab)=0,p[2](abc)=0,p[3](abca,a相同）=1，p[4](abcab,ab相同）=2，p[5](abcabc,abc相同)=3
2,思路
那么我们怎么求解该函数呢
首先，我们发现p[i+1]<=p[i]+1,当且仅当s[i+1]==s[p[i]]（字符串s下标从0开始）时等号成立
那么，我们思考不等于怎么求解：
我们尝试让前缀和减少一点，即j=p[i]-1,再次比较是否s[i+1]==s[j],如果相等有s[0....j ]==s[ i+1-j.....i+1 ]==s[ p[i]-1-j....p[i]-1]，我们会发现，这样把范围从i变成p[i]-1
如果长度j不行，我们可以继续让j=p[j-1],直到j=0，若还是s[i+1]!=s[p[j]](就是s[0])，那么p[i+1]=0
结合上述思想，我们会得到十分简洁的代码
string a;
cin >> a;
p[0] = 0;//只有一个字符，当然为0
for (int i = 1; i < (int)a.size(); ++i)//从2个字符以上开始（i=1开始）
{
int j = p[i - 1];//每次都先取上一次i-1长度的最长前缀长度，接下来判断是否s[i]==s[j],因为下标从0开始，j是长度，所以j刚好就是最长前缀的下一位，如果判断两者相同，不用走while，直接j+1
while (j > 0 && a[i] != a[j])j = p[j-1];//如果不相等，范围缩小为p[j-1],j-1是比原来前缀少1，p[j-1]就是在这个前缀范围找前缀，如果为0，就是没有前缀，所以为0跳出（用j>0限制）
if (a[i] == a[j])++j;//如果出来（没进去while也一样）相等，说明下一位相同，j+1
p[i] = j;//存储p[i+1]
}二，KMP算法
1，定义
KMP可以解决寻找字符串中特定子串等等问题
2，思路
其实，在我们理解完前缀函数，基本就差一步就学会KMP算法了
kmp如何快速判断子串呢，其实运用到与前缀函数相似的跳跃思想
我们在s1中寻找s2，已经匹配到第5个了，但是x，y不相等，KMP的思路是直接将前缀移动到后缀的位置，继续匹配，中间的直接跳过
i1,i2为两个串当前指向位置，我们跳跃后，继续比对i1，i2指向位置。
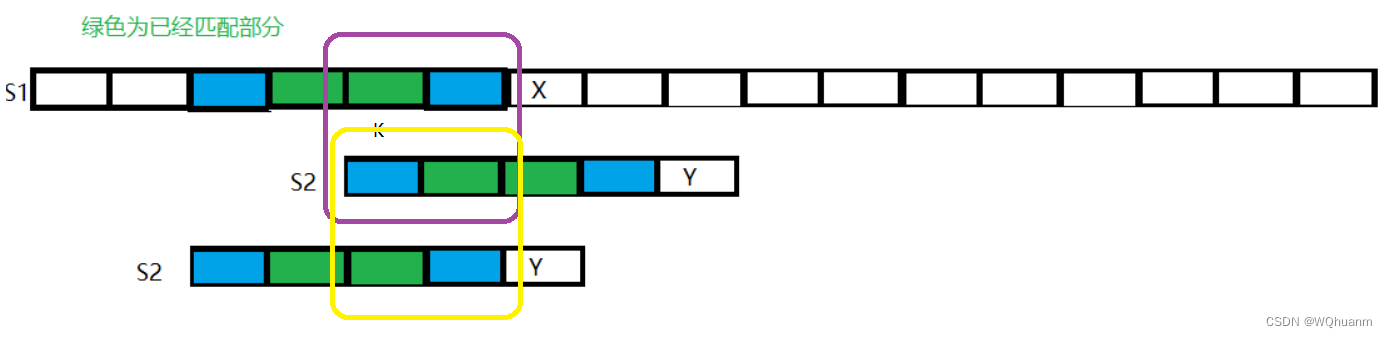为什么可以跳过中间呢，我们假设从中间的k位置也可以匹配成功 ，那么至少紫色框中是可以相等的，那我们发现，黄色框也必须相等。这时候，你会发现，最长前缀变大了，矛盾，这就是为什么移动到最长缀匹配的位置
kmp同样简洁（时间复杂度0（n+m))
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 100;
int p[N];
int main()
{
string a, b;
cin >> a >> b;
//前缀函数
p[0] = 0;
for (int i = 1; i < (int)b.size(); ++i)
{
int j = p[i - 1];
while (j > 0 && b[i] != b[j])j = p[j - 1];
if (b[i] == b[j])++j;
p[i] = j;
}
//kmp
int j = 0;//j指针指向b字符串
for (int i = 0; i < (int)a.size(); ++i)//i指针指向a字符串
{
while (j > 0 && a[i] != b[j])j = p[j - 1];//如果不相等，跳跃，当然j>0(即j指针不是指向b串第一个字符时），i与j是当前比对的位置，我们跳跃是前面成功匹配的j-1部分
if (a[i] == b[j])++j;//出来成功匹配，j往前
if (j == (int)b.size())cout << i - j + 2 << endl;//如果j为b长度，说明符合，输出a匹配b的第一个位置，继续往下寻找，不需要重置j，因为下一次进入，while比较是j指向\0,自然会跳跃
}
return 0;
}三，一道模板P3375 【模板】KMP字符串匹配
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 100;
int p[N];
int main()
{
string a, b;
cin >> a >> b;
//前缀函数
p[0] = 0;
for (int i = 1; i < (int)b.size(); ++i)
{
int j = p[i - 1];
while (j > 0 && b[i] != b[j])j = p[j - 1];
if (b[i] == b[j])++j;
p[i] = j;
}
//kmp
int j = 0;//j指针指向b字符串
for (int i = 0; i < (int)a.size(); ++i)//i指针指向a字符串
{
while (j > 0 && a[i] != b[j])j = p[j - 1];//如果不相等，跳跃，当然j>0(即j指针不是指向b串第一个字符时），i与j是当前比对的位置，我们跳跃是前面成功匹配的j-1部分
if (a[i] == b[j])++j;//出来成功匹配，j往前
if (j == (int)b.size())cout << i - j + 2 << endl;//如果j为b长度，说明符合，输出a匹配b的第一个位置，继续往下寻找，不需要重置j，因为下一次进入，while比较是j指向\0,自然会跳跃
}
for (int i = 0; i < (int)b.size(); ++i)
{
cout << p[i];
if (i == (int)b.size() - 1)cout << endl;
else cout << ' ';
}
return 0;
}
