第一部分 多头注意力
// 待更
第二部分 LLaMA2之分组查询注意力——Grouped-Query Attention
自回归解码的标准做法是缓存序列中先前标记的键 (K) 和值 (V) 对,从而加快注意力计算速度
然而,随着上下文窗口或批量大小的增加,多头注意力 (MHA)模型中与 KV 缓存大小相关的内存成本显着增长
对于较大的模型,KV 缓存大小成为瓶颈,键和值投影可以在多个头之间共享,而不会大幅降低性能,可以使用
- 具有单个 KV 投影的原始多查询格式(MQA)
ChatGLM2-6B即用的这个,详见此文《ChatGLM两代的部署/微调/实现:从基座GLM、ChatGLM的LoRA/P-Tuning微调、6B源码解读到ChatGLM2的微调与实现》的3.1.2节
不过,多查询注意(Multi-query attention,简称MQA)只使用一个键值头,虽大大加快了解码器推断的速度,但MQA可能导致质量下降,而且仅仅为了更快的推理而训练一个单独的模型可能是不可取的 - 或具有多个 KV 投影的分组查询注意力(grouped-query attention,简称GQA),速度快 质量高
23年,还是Google的研究者们提出了一种新的方法,即分组查询注意(GQA,论文地址为:GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints),这是一种多查询注意的泛化,它通过折中(多于一个且少于查询头的数量,比如4个)键值头的数量,使得经过强化训练的GQA以与MQA相当的速度达到接近多头注意力的质量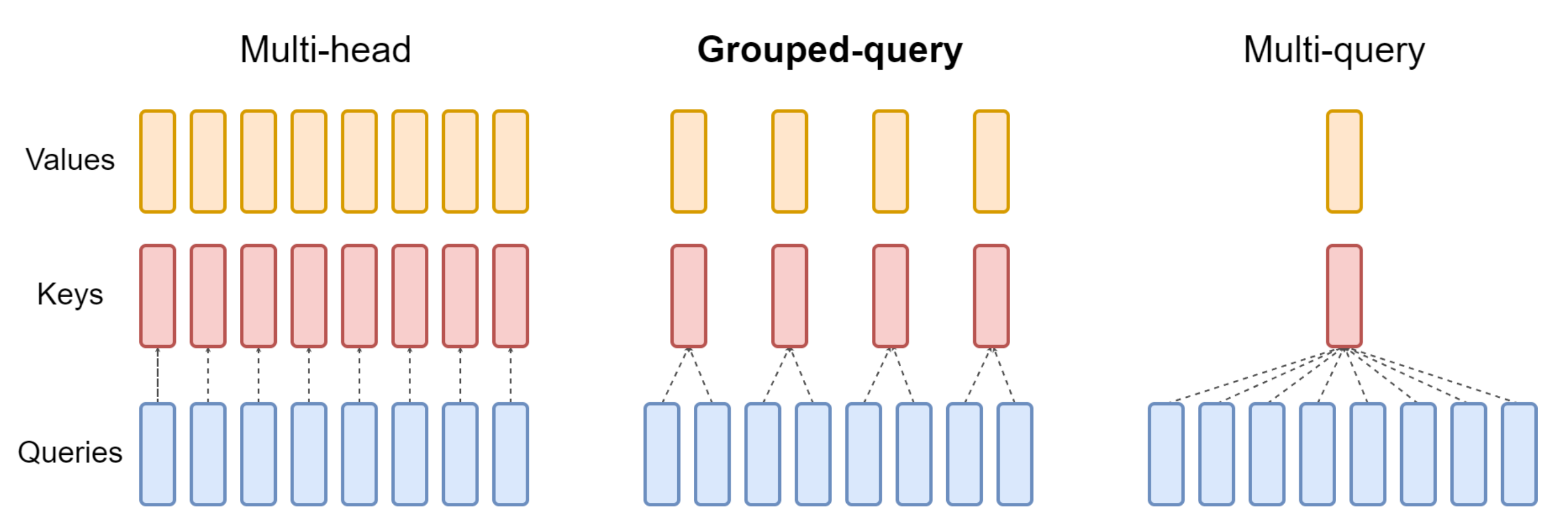
经实验论证,GQA 变体在大多数评估任务上的表现与 MHA 基线相当,并且平均优于 MQA 变体
第三部分 多查询注意力(Muti Query Attention)
3.1 MQA的核心特征:各自Query矩阵,但共享Key 和 Value 矩阵
多查询注意力(Muti Query Attention)是 19 年Google一研究者提出的一种新的 Attention 机制(对应论文为:Fast Transformer Decoding: One Write-Head is All You Need、这是其解读之一),其能够在保证模型效果的同时加快 decoder 生成 token 的速度
那其与17年 Google提出的transformer中多头注意力机制(简称MHA)有啥本质区别呢?有意思的是,区别在于:

- 我们知道MHA的每个头都各自有一份不同的Key、Query、Value矩阵
- 而MQA 让所有的头之间 共享 同一份 Key 和 Value 矩阵,每个头只单独保留了一份 Query 参数,从而大大减少 Key 和 Value 矩阵的参数量
总之,MQA 实际上是将 head 中的 key 和 value 矩阵抽出来单独存为一份共享参数,而 query 则是依旧保留在原来的 head 中,每个 head 有一份自己独有的 query 参数
下图对比了多头注意力(Multi-Head Attention)、LLaMA2中分组查询注意力(Grouped-Query Attention)、多查询注意力(Muti Query Attention)的差别

总之,MHA 和 MQA 之间的区别只在于建立 Wqkv Layer 上
# Multi Head Attention
self.Wqkv = nn.Linear( # 【关键】Multi-Head Attention 的创建方法
self.d_model,
3 * self.d_model, # 有 query, key, value 3 个矩阵, 所以是 3 * d_model
device=device
)
query, key, value = qkv.chunk( # 【关键】每个 tensor 都是 (1, 512, 768)
3,
dim=2
)
# Multi Query Attention
self.Wqkv = nn.Linear( # 【关键】Multi-Query Attention 的创建方法
d_model,
d_model + 2 * self.head_dim, # 只创建 query 的 head 向量,所以只有 1 个 d_model
device=device, # 而 key 和 value 不再具备单独的头向量
)
query, key, value = qkv.split( # query -> (1, 512, 768)
[self.d_model, self.head_dim, self.head_dim], # key -> (1, 512, 96)
dim=2 # value -> (1, 512, 96)
)对比上面的代码,你可以发现
- 在 MHA 中,query, key, value 每个向量均有 768 维度
- 而在 MQA 中,只有 query 是 768 维,而 key 和 value 均只剩下 96 维了,恰好是 1 个 head_dim 的维度
因此,可以确认:在 MQA 中,除了 query 向量还保存着 8 个头,key 和 value 向量都只剩 1 个「公共头」了,这也正好印证了论文中所说的「所有 head 之间共享一份 key 和 value 的参数」
剩下的问题就是如何将这 1 份参数同时让 8 个头都使用,代码里使用矩阵乘法 matmul 来广播,使得每个头都乘以这同一个 tensor,以此来实现参数共享:
def scaled_multihead_dot_product_attention(
query,
key,
value,
n_heads,
multiquery=False,
):
q = rearrange(query, 'b s (h d) -> b h s d', h=n_heads) # (1, 512, 768) -> (1, 8, 512, 96)
kv_n_heads = 1 if multiquery else n_heads
k = rearrange(key, 'b s (h d) -> b h d s', h=kv_n_heads) # (1, 512, 768) -> (1, 8, 96, 512) if not multiquery
# (1, 512, 96) -> (1, 1, 96, 512) if multiquery
v = rearrange(value, 'b s (h d) -> b h s d', h=kv_n_heads) # (1, 512, 768) -> (1, 8, 512, 96) if not multiquery
# (1, 512, 96) -> (1, 1, 512, 96) if multiquery
attn_weight = q.matmul(k) * softmax_scale # (1, 8, 512, 512)
attn_weight = torch.softmax(attn_weight, dim=-1) # (1, 8, 512, 512)
out = attn_weight.matmul(v) # (1, 8, 512, 512) * (1, 1, 512, 96) = (1, 8, 512, 96)
out = rearrange(out, 'b h s d -> b s (h d)') # (1, 512, 768)
return out, attn_weight, past_key_value