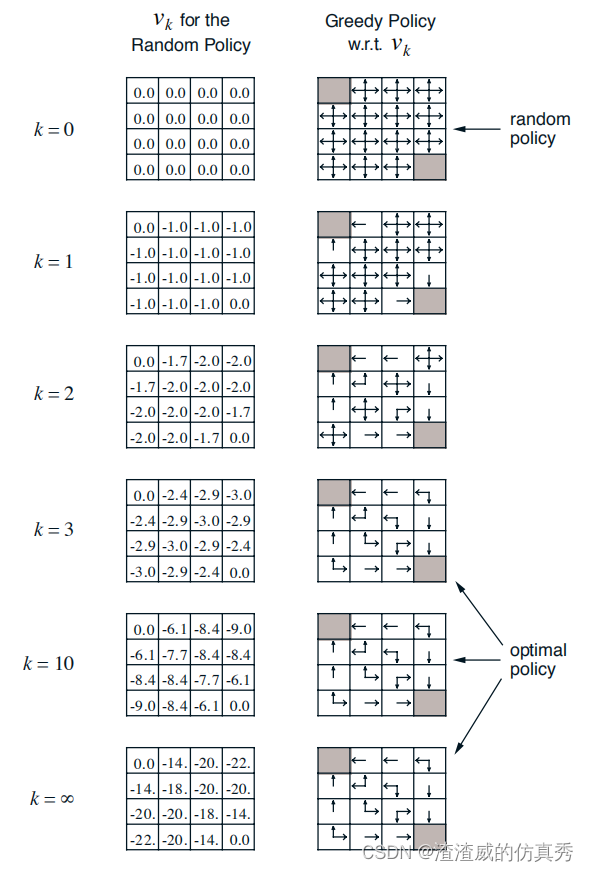
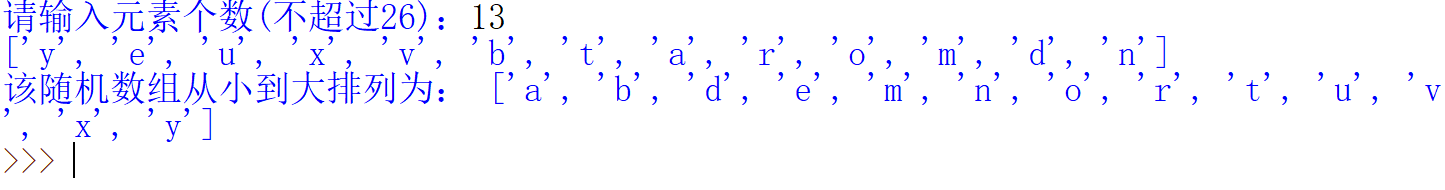先更新前两道题目，下午更新后两道

两道模板题(拓扑排序)

拓扑排序

拓扑排序（Topological Sorting）：一种对有向无环图（DAG）的所有顶点进行线性排序的方法，使得图中任意一点 $u$ 和 $v$，如果存在有向边 $<u, v>$，则 $u$ 必须在 $v$ 之前出现。对有向图进行拓扑排序产生的线性序列称为满足拓扑次序的序列，简称拓扑排序。

拓扑排序解决的主要问题？

拓扑排序可以用来解决一些依赖关系的问题，比如项目的执行顺序，课程的选修顺序等。

 

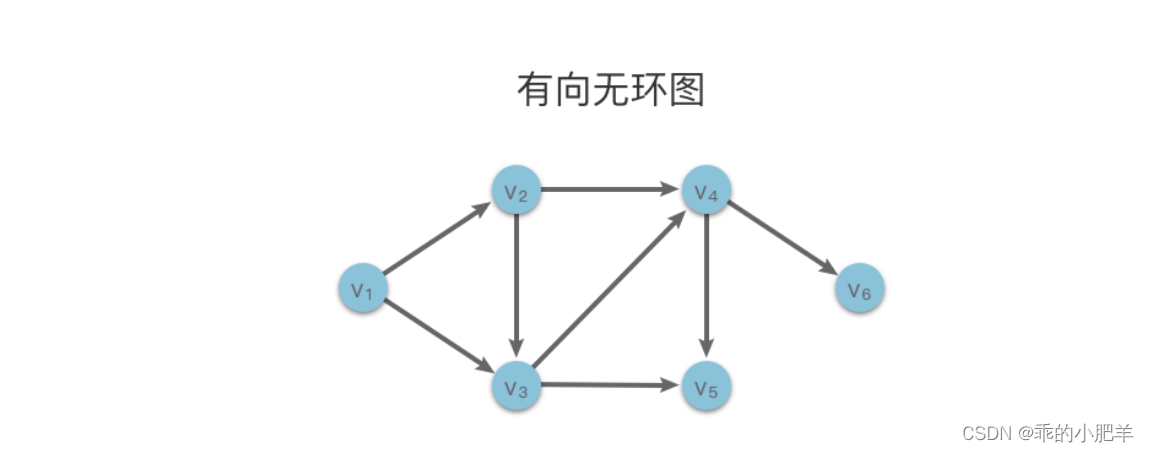
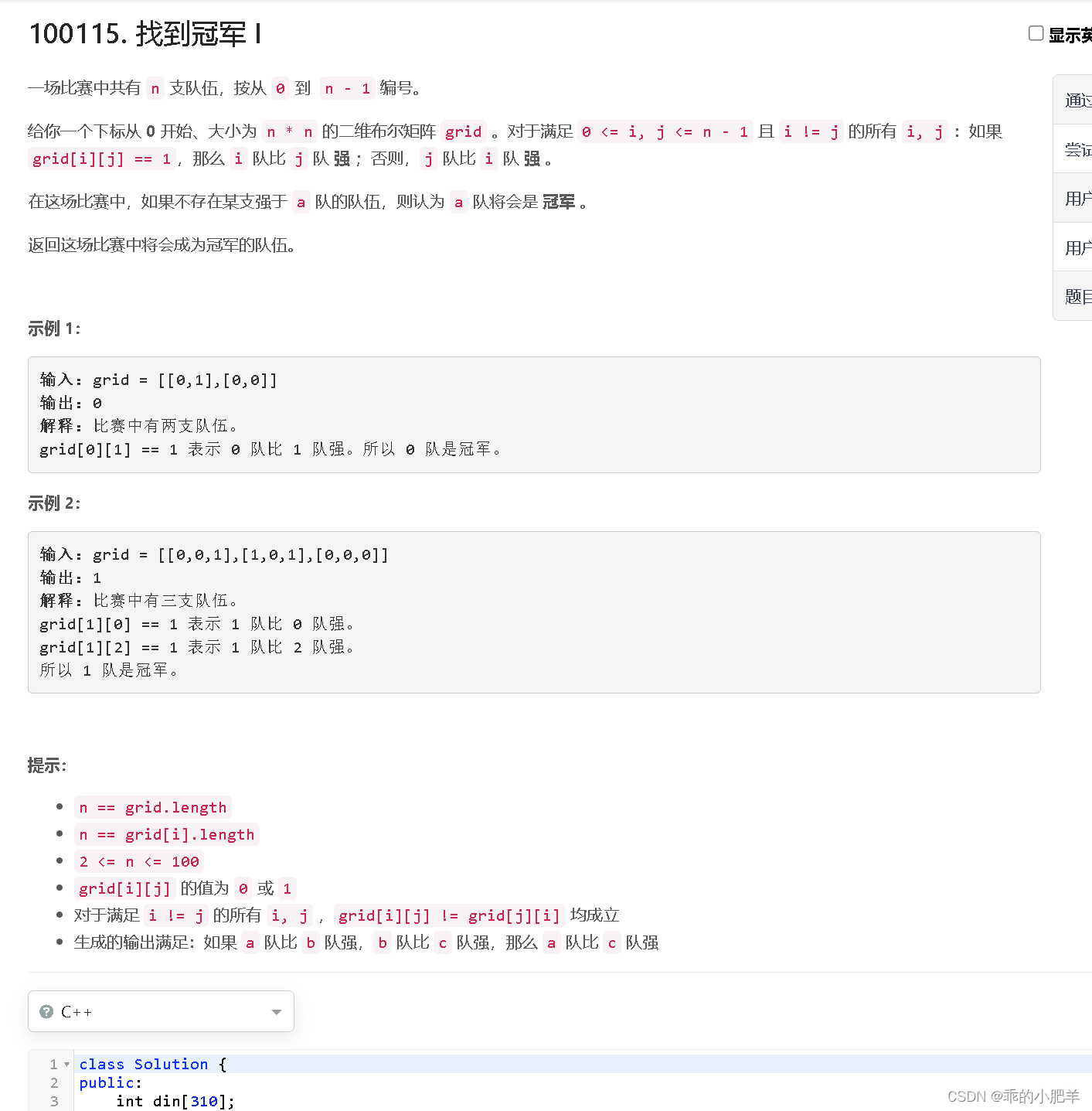
 刚开始我的思路是，先想的是并查集，但是看了第二题(提示有向无环图)就先想拓扑排序了，第一道题的代码复制一下到第二题基本就可以解决第二道题

 差分约束应该也是可以实现的

 但是我这里采用更为简单的做法，拓扑排序

 拓扑排序可以解决一系列具有依赖关系的问题，例如家谱树，课程表等等问题

 前三题为板子题

class Solution {
public:
    int din[310];
    int dou[310];
    int h[11010],ne[11010],e[11010],idx;
    queue<int> q;
    int sort_d[110];
    int sid = 0;
    void top_sort(int n)
    {
        for(int i = 0;i < n;i++)
        {
            if(!din[i]) q.push(i);
        }
        
        while(!q.empty())
        {
           auto t = q.front();
           q.pop();
           sort_d[sid++] = t;
           for(int i = h[t];i != -1;i = ne[i])
           {
               int b = e[i];//i是对应点的虚拟编号(相当于索引),正式编号是e[i]
               din[b]--;
               if(!din[b])
               {
                   q.push(b);
               }
           }
        }
    }
    void add(int a,int b)
    {
        e[idx] = b,ne[idx] = h[a],h[a] = idx++;
    }
    int findChampion(vector<vector<int>>& grid) 
    {
        int n = grid.size();
        
        memset(h,-1,sizeof(h));
        memset(sort_d,-1,sizeof(sort_d));
        for(int i = 0;i < n;i++)
        {
            for(int j = 0;j < n;j++)
            {
                if(i != j)
                {
                   int a_team = i;
                   int b_team = j;
                   if(grid[i][j])
                   {
                     //a队强
                     din[b_team]++;
                     dou[a_team]++;
                     add(a_team,b_team);
                   }
                   else
                   {
                      //b队强
                     din[a_team]++;
                     dou[b_team]++;
                     add(b_team,a_team);
                   }
                }
            }
        }
        
        top_sort(n);
        if(sort_d[0] == -1) return -1;
        return sort_d[0];
    }
};

 第二题也是板子题，跟第一题没什么区别，复制第一题的代码改一下就行了

class Solution {
public:
    int din[310];
    int dou[310];
    int h[111010],ne[111010],e[111010],idx;
    queue<int> q;
    int sort_d[110];
    int sid = 0;
    bool flag = false;
    void top_sort(int n)
    {
        for(int i = 0;i < n;i++)
        {
            if(!din[i]) q.push(i);
        }
        if(q.size() > 1)
        {
            flag = true;
            return ;
        }
        while(!q.empty())
        {
           auto t = q.front();
           q.pop();
           sort_d[sid++] = t;
           for(int i = h[t];i != -1;i = ne[i])
           {
               int b = e[i];//i是对应点的虚拟编号(相当于索引),正式编号是e[i]
               din[b]--;
               if(!din[b])
               {
                   q.push(b);
               }
           }
        }
    }
    void add(int a,int b)
    {
        e[idx] = b,ne[idx] = h[a],h[a] = idx++;
    }
    int findChampion(int n,vector<vector<int>>& edge) 
    {
        
        memset(h,-1,sizeof(h));
        memset(sort_d,-1,sizeof(sort_d));
        int size_edge = edge.size();
        for(int i = 0;i < edge.size();i++)
        {
            int a = edge[i][0];
            int b = edge[i][1];
            //a队强
            add(a,b);
            din[b]++;
            dou[a]++;
        }
        top_sort(n);
        

        if(flag) return -1;
        return sort_d[0];
    }
};