目录
1、绪论
2、线性表
3、栈、队列和数组
4、串
5、树与二叉树
6、图
7、查找
8、排序
1、绪论
什么是数据结构?
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。数据结构包括三个方面:逻辑结构、存储结构、数据的运算。
逻辑结构有:集合(数据元素除属于“同一个集合”外,别无其他关系);
线性结构(数据元素之间只存在一对一的关系);
树形结构(数据元素之间存在一对多的关系);
图状结构或网状结构(数据元素之间存在多对多的关系)。
存储结构有:顺序存储、链式存储、索引存储、散列存储。
四种存储结构的优缺点是什么?
顺序存储:
优点:可以实现随机存取,每个元素占用最少的存储空间;
缺点:只能使用相邻的一整块存储单元,因此可能产生较多的外部碎片。
链式存储:
优点:不会出现碎片现象,能充分利用所有存储单元;
缺点:每个元素因存储指针而占用额外的存储空间,且只能实现顺序存取。
索引存储:
优点:检索速度快;
缺点:附加的索引表额外占用存储空间。另外,增加和删除数据时也要修改索引表,
因而会花费较多的时间。
散列存储:
优点:检索、增加和删除结点的操作都很快;
缺点:若散列函数不好,则可能出现存储单元的冲突,而解决冲突会增加时间和空间的开销。
算法的基本概念?
算法(Algorithm)是对特定问题求解步骤的一种描述。
算法的五个特性:
有穷性、确定性、可行性、输入、输出。
“好”算法应达到以下目标:
正确性、可读性、健壮性、高效率与低存储量需求。
时间复杂度的计算?
点击跳转到时间复杂度的计算
常见的渐近时间复杂度为
O(1)<O(logn)<O(n)<O(nlogn)<O(
)<O(
)<O(
)<O(n!)<O(
)
2、线性表
顺序表在插入或删除时一般需要移动元素,如果想不移动多个元素就实现插入和删除,应该如何处理?
插入元素时,直接将新元素插入在第n+1个位置;删除第i个元素时,将第n个元素补到第i个位置。
请简要说明线性表的顺序存储结构和链式存储结构在数据插入、数据删除、数据查找、存储空间占用等方面的优缺点。
顺序表在插入和删除时需要移动很多数据,时间耗费高;而链式存储不需要移动数据,时间耗费低。
顺序表分配空间的大小不好确定,要根据经验;而链式存储时按照需要分配,不会浪费空间。
顺序表查找元素时,支持用下标查找,时间耗费低;链式存储方式查找时只能从前往后顺序进行查找和比较,时间耗费高。
链式存储结构中,头指针和头结点之间的区分?引入头结点有什么优点呢?
不管带不带头结点,头指针都始终指向链表的第一个结点,而头结点是带头结点的链表中的第一个结点,结点内通常不存储信息。
引入头结点后,可以带来两个优点:
①由于第一个数据结点的位置被存放在头结点的指针域中,因此在链表的第一个位置上的操作和在表的其他位置上的操作一致,无须进行特殊处理。
②无论链表是否为空,其头指针都是指向头结点的非空指针(空表中头结点的指针域为空),因此空表和非空表的处理也就得到了统一。
循环双链表的判空条件是什么?
当循环双链表为空表时,head->next=head 并且 head->prior=head;
3、栈、队列和数组
说明线性表、栈和队列的异同点?
相同点:
都是线性结构,都是逻辑结构的概念。都可以用顺序存储和链式存储。
不同点:
①运算规则不同,线性表支持随机存取。栈只允许在一端进行插入、删除运算,因而是后进先出(LIFO)。队列是只允许一端进行插入,另一端进行删除运算,因而是先进先出(FIFO)。
②用途不同,栈用于子程调用和保护现场。队列用于多道作业处理、指令寄存及其他运算等。
栈初始化是栈顶指针S.top==-1,栈空和栈满的条件是什么?
栈空:S.top==-1
栈满:S.top==MaxSize-1
共享栈两个栈顶指针都指向栈顶元素,第一种情况top0=-1时0号栈为空,top1=MaxSize时1号栈为空。第二种情况top0=0时0号栈为空,top1=MaxSize-1时1号栈为空。判满条件分别是什么?
判满条件:
第一种:top1-top0==1(两个指针相邻,因为插入时先移指针再插入元素)
第二种:top0-top1==1(两个指针错开相邻,因为插入时先插入元素再移动指针)
当1、2、3、4顺序进栈时,列出所有可能的出栈顺序?
有14种(
用卡特兰数计算)
①全进之后再出,只有1种:4321
②进三个开始出,只有3种:3421、3241、3214
③进二个开始出,只有5种:2431、2341、2134、2143、2134
④进一个开始出,只有5种:1431、1324、1342、1234、1243
顺序队列的入队出现“假上溢/假溢出”是怎样产生的?解决途径是什么?为了区分队空还是队满的情况,有哪三种处理方式?
一般的一维数组队列的尾指针已经到了数组的上界,不能再有入队操作,但其实数组中还有空位置,这就叫“假溢出”。采用循环队列是解决假溢出的途径。
为了区分是队空还是队满的情况,有三种处理方式:
①牺牲一个单元来区分队空还是队满入队时少用一个队列单元,这是一种较为普遍的做法。队满条件:(Q.rear+1)%MaxSize==Q.front。队空条件:Q.rear==Q.front。队列中元素的个数:(Q.rear-Q.front+MaxSize)%MaxSize。
②类型中增设表示元素个数的数据成员。这样,队空的条件为Q.size==0;堆满的条件是Q.size==MaxSize。这两种情况都有Q.front==Q.rear。
③类型中增设tag数据成员,以区分是队满还是队空。tag等于0时,若因删除导致Q.front==Q.rear,则为队空;tag等于1时,若因插入导致Q.front==Q.rearz,则为堆满。
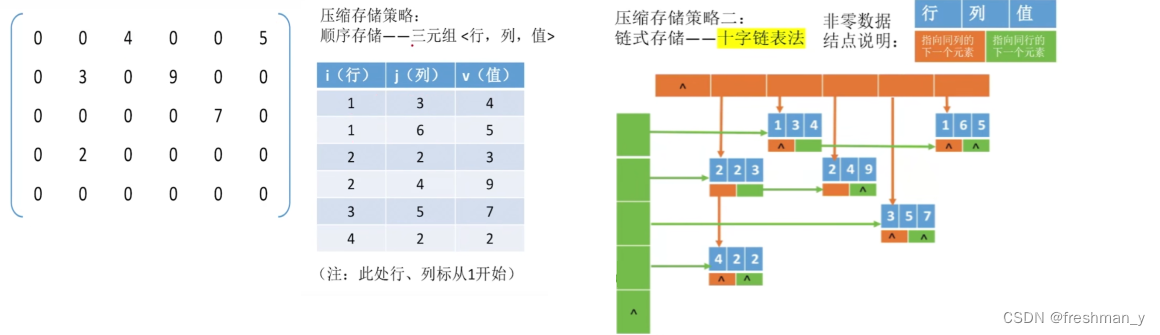
稀疏矩阵压缩存储策略有哪两种?
链式存储:十字链表法。
顺序存储:三元组<i(行),j(列),v(值)>,失去了数组随机存储的特性。
将稀疏矩阵换成对应的三元组(行列从0,0或者从1,1开始记得备注清楚),将稀疏矩阵转为十字链表呢?反向转换成稀疏矩阵呢?
广义表会基本操作?
考点:
①求表头(取第一个元素)
②求表尾(除去第一个元素)
③求长度(所含元素个数)
④求深度(数左括号或右括号个数)
例1:广义表((a,b,c,d))的表头是(a,b,c,d) 表尾是 ()
例2:广义表L=((a,b,c)),则L的长度和深度分别是 1 和 2
例3:广义表L=(a,(b,c)),进行Tail(L)操作后结果是 ((b,c))
//例4从最里层函数往外求
例4:广义表A=(a,b,(c,d),(e,(f,g))),则Head(Tail(Head(Tail(Tail(A)))))的值为 d
画出广义表(a,(x,y),((x)))的存储结构 ?
4、串
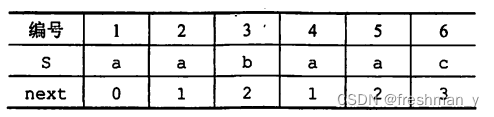
设有主串S='aabaabaabaac',模式串P='aabaac'。(1)求出P的next数组。(2)试给出KMP算法的匹配过程。
(1)P的next数组如下所示:
(2)KMP算法的匹配过程如下:
串'ababaaababaa'的nextval数组为?
5、树与二叉树
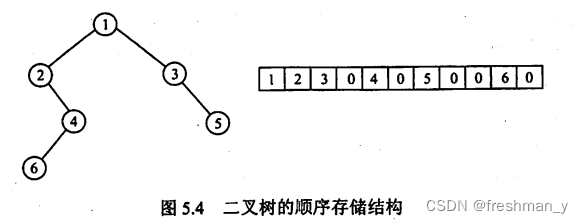
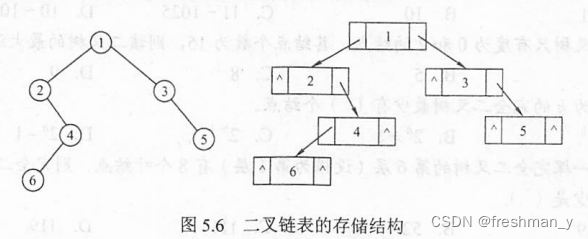
一棵二叉树分别用顺序存储和链式存储表示?
注:其中0表示不存在的空结点,数组存储的开始下标建议从1开始。
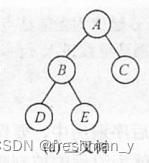
试写出如图所示的二叉树分别按先序、中序、后序、层序遍历时得到的结点序列?
先序:ABDEC
中序:DBEAC
后序:DEBCA
层序:ABCDE
由遍历序列构造二叉树(三种情况:先序和中序、后序和中序、层序和中序 )?关键点:先确定根,然后通过中序分左右子树
例如:求先序序列(ABCDEFGHI)和中序序列(BCAEDGHFI)所确定的二叉树
请画出与下面二叉树相对应的中序线索二叉链表(不带头结点)?
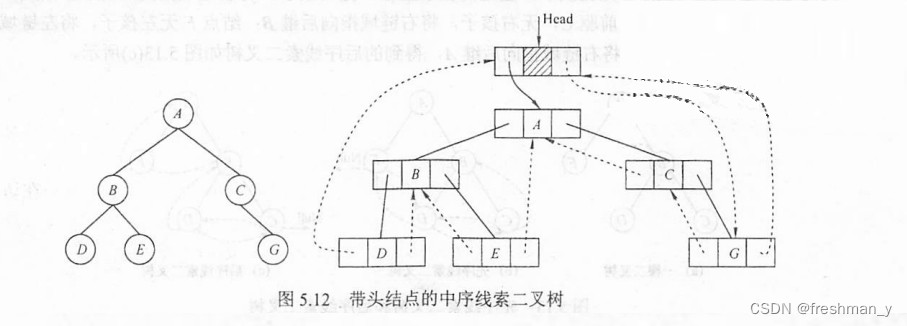
请画出与下面二叉树相对应的中序线索二叉树链式存储结构(带头结点)?
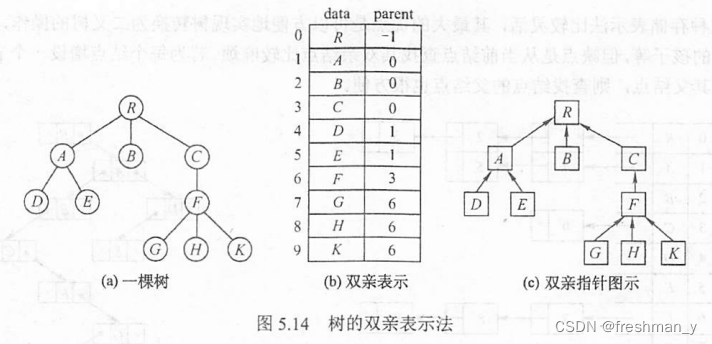
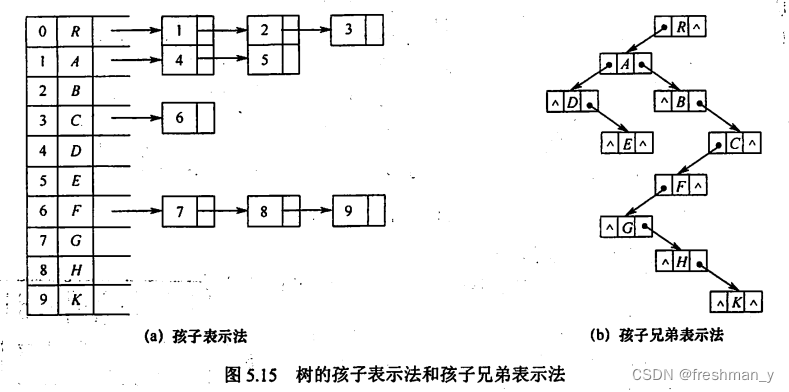
一棵树双亲表示法、孩子表示法、孩子兄弟表示法怎么表示 ?
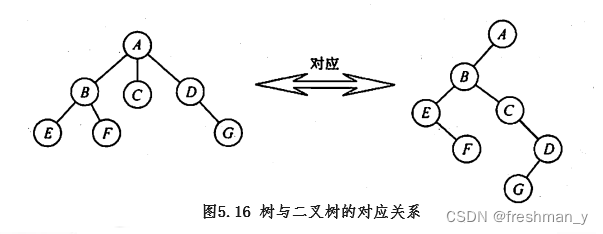
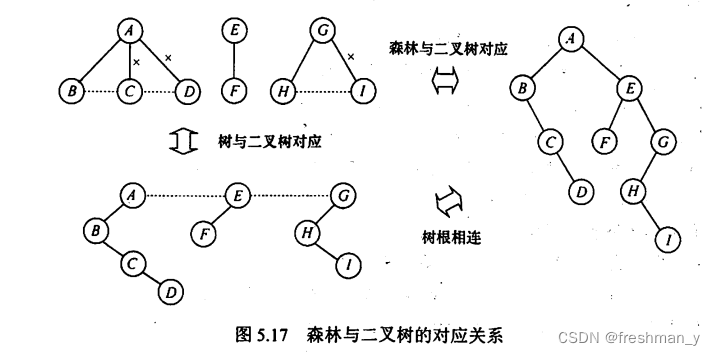
用“左孩子右兄弟”的方法将一棵树转换为二叉树?将森林转换成一棵二叉树?
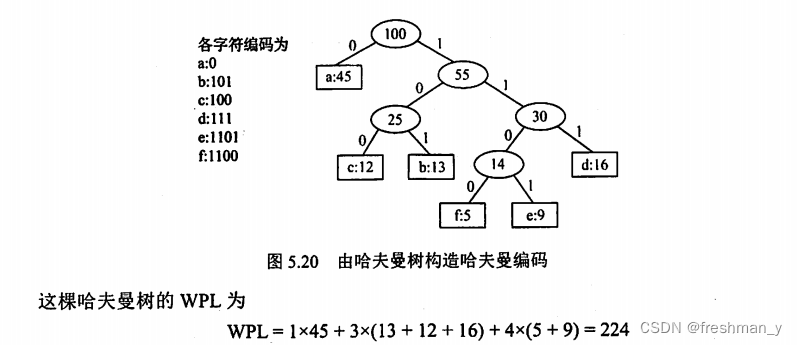
哈夫曼树如何构造?带权路径长度(WPL)是多少?各个字符编码为?
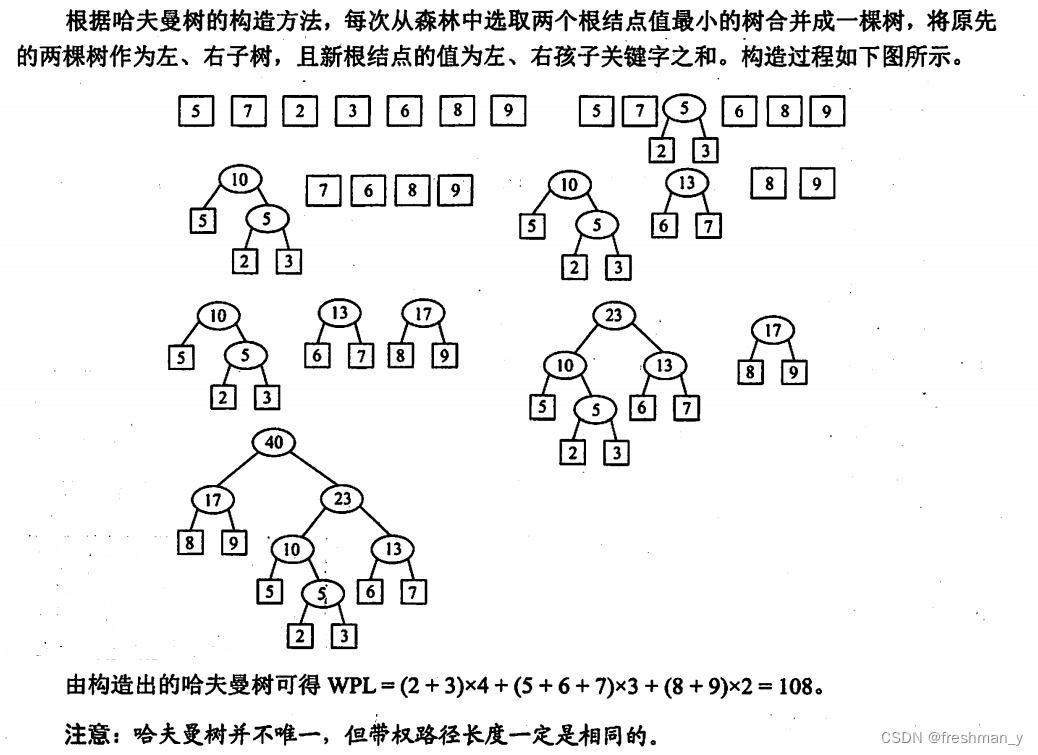
设给定权集w={5,7,2,3,6,8,9},试构造关于w的一棵哈夫曼树,并求其加权路径长度WPL。
6、图
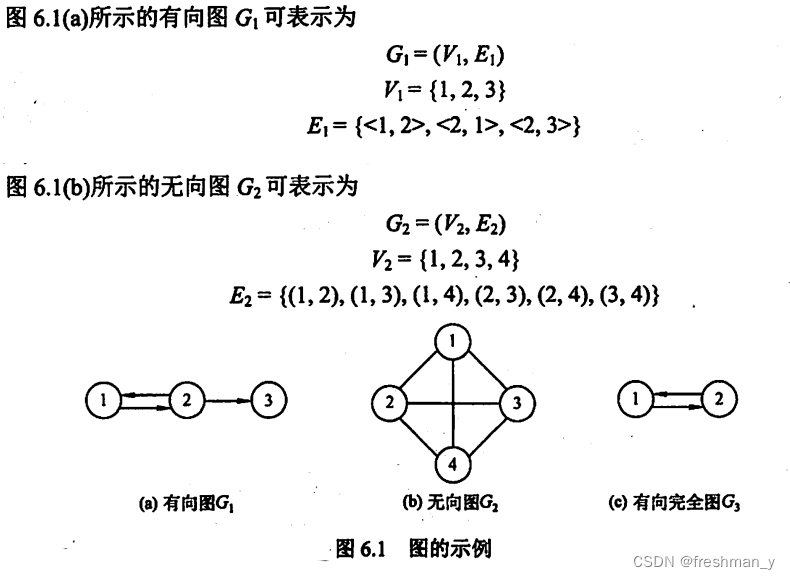
已知道图的顶点和边的集合时,能画出图的形状?
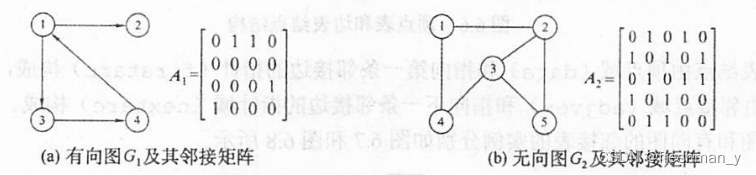
已知有向图和无向图,画出对应的邻接矩阵?
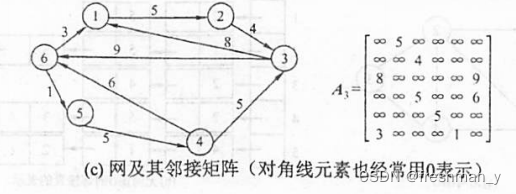
带权图的邻接矩阵怎么画呢?
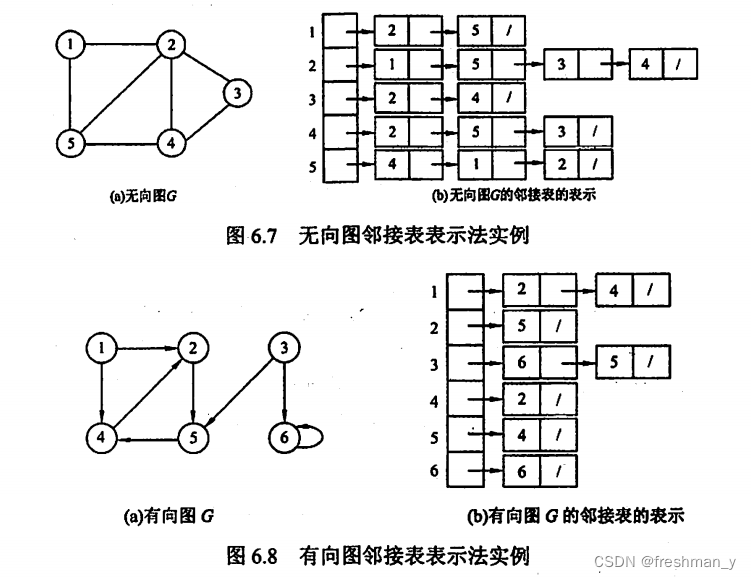
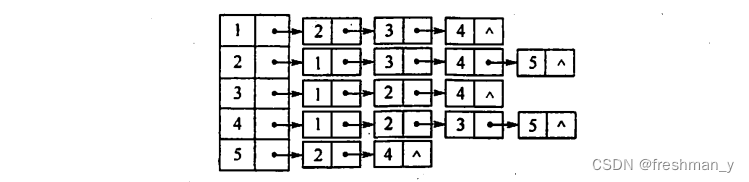
已知道有向图和无向图,让你画出对应的邻接表你会画吗?
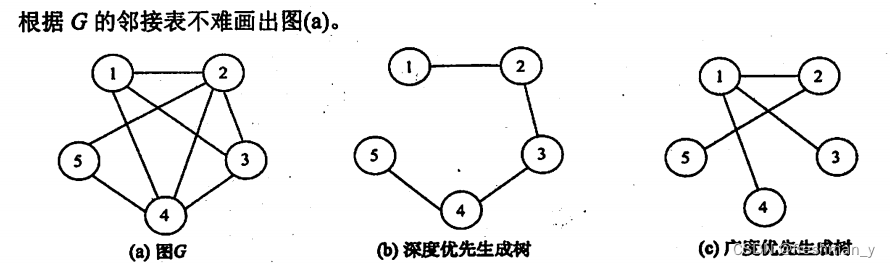
图G=(V,E)以邻接表存储,如下图所示,试画出图G的深度优先生成树和广度优先生成树(假设从结点1开始遍历),深度优先序列和广度优先序列呢?
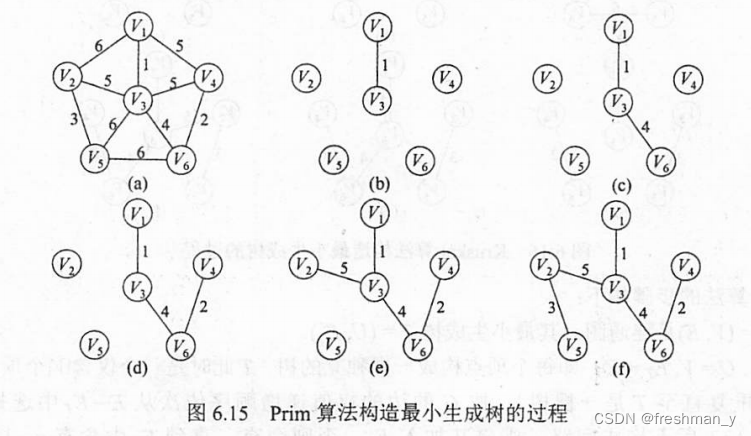
如何使用Prim算法构造最小生成树,给出构造过程?
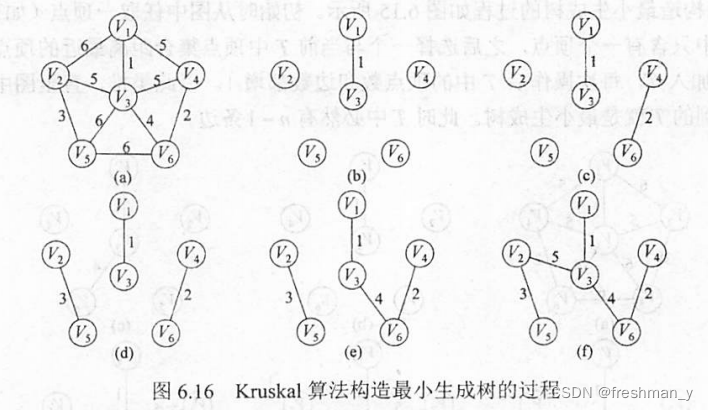
如何使用Kruskal算法构造最小生成树,给出构造过程?
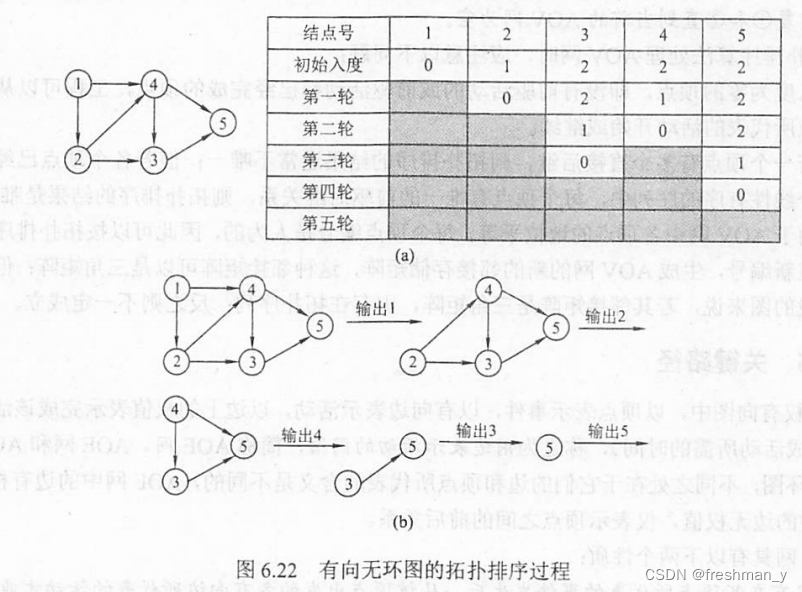
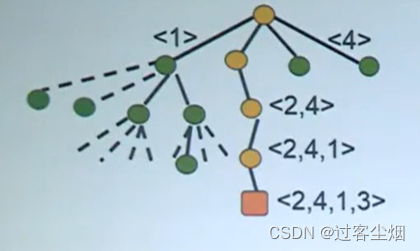
给定一个有向无环图,让写出拓扑排序的结果为?
以下图的拓扑排序结果为{1,2,4,3,5}
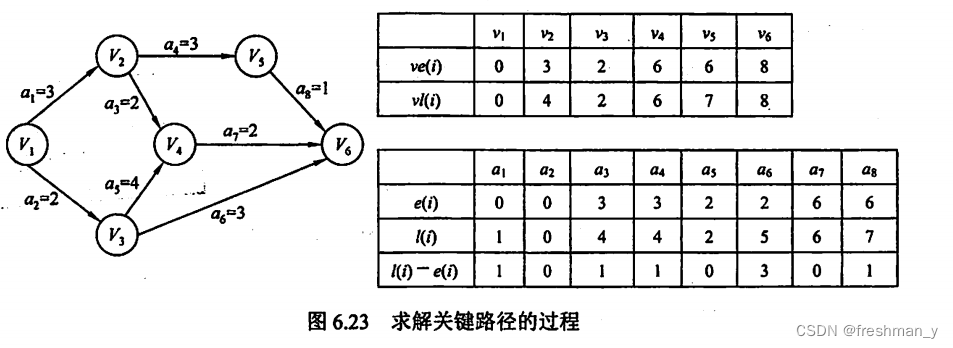
给定一个AOE网,求出其关键路径,该工程完成的最少时间?
关键路径为(v1,v3,v4,v6),最少时间为a2+a5+a7=8
7、查找
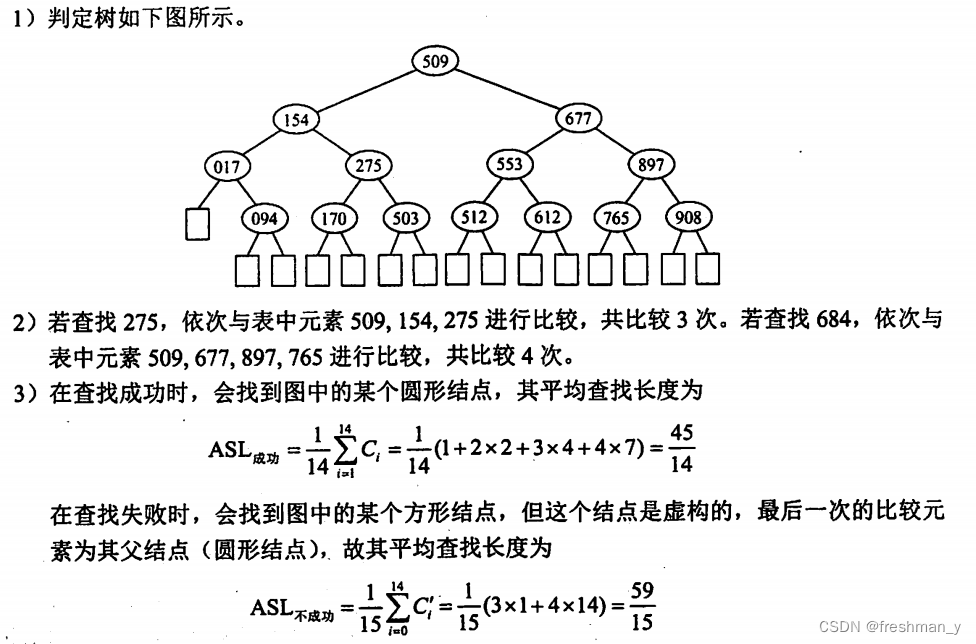
有序顺序表中的元素依次为017,094,154,170,275,503,509,512,553,612,677,765,897,908。1)试画出对其进行折半查找的判定树。2)若查找275或684的元素,将依次与表中的哪些元素比较?3)计算查找成功的平均查找长度和查找不成功的平均查找长度。
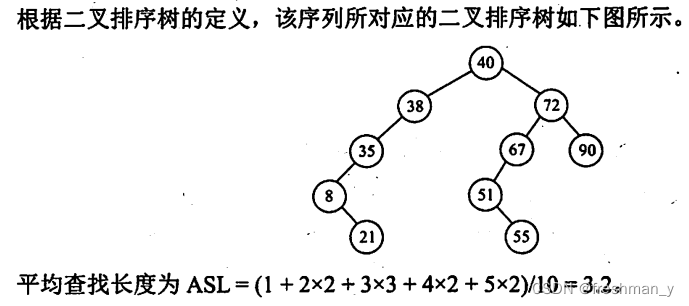
按照序列{40,72,38,35,67,51,90,8,55,21}建立一棵二叉排序树,画出该树,并求出在等概率的情况下,查找成功的平均查找长度。
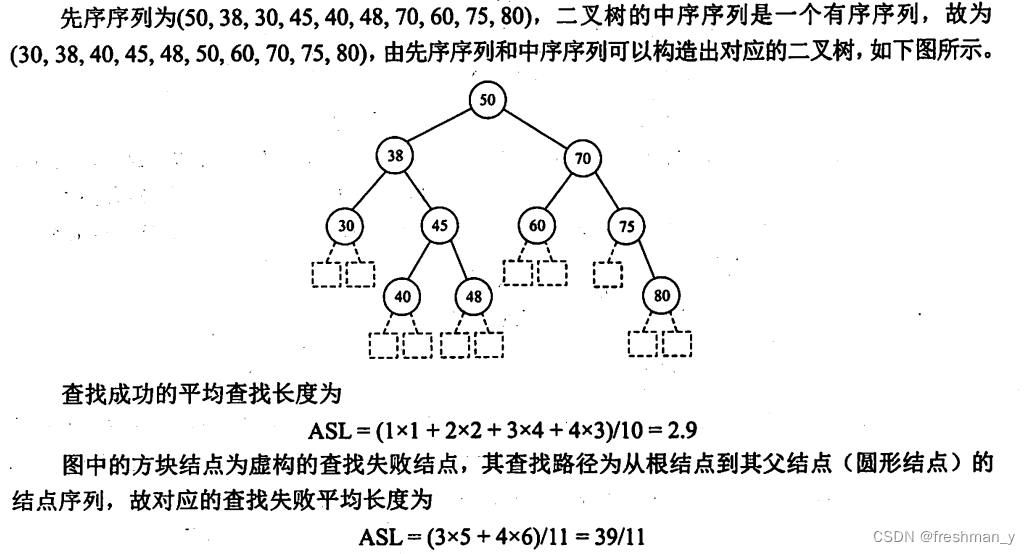
一棵二叉树按先序遍历得到的序列为(50,38,30,45,40,48,70,60,75,80),试画出该二叉排序树,并求出等概率下查找成功和查找失败的平均查找长度。
给定一个关键字集合{25,18,34,9,14,27,42,51,38},假定查找各关键字的概率相同,请画出其最佳排序树。
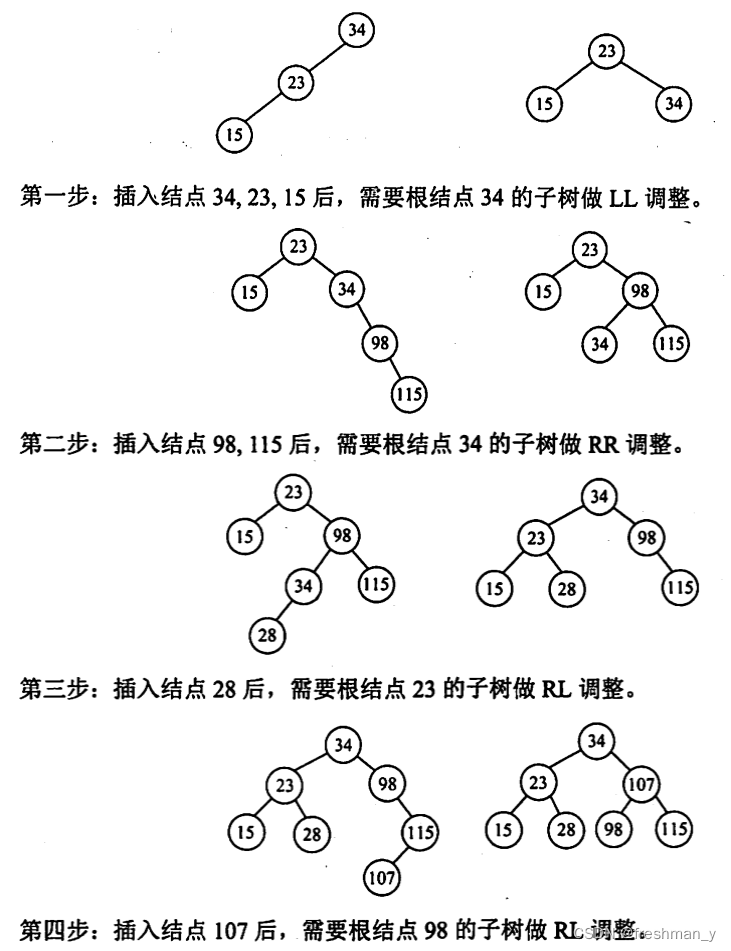
依次把结点(34,23,15,98,115,28,107)插入初始状态为空的平衡二叉排序树,使得在每次插入后保持该树仍然是平衡二叉树。请依次画出每次插入后所形成的平衡二叉排序树。
使用散列函数H(key)=key%11,把一个整数值转换成散列表下标,现在要把数据{1,13,12,34,38,33,27,22}依次插入散列表。1)使用线性探测法来构造散列表。2)使用链地址法构造散列表。试针对这两种情况,分别确定查找成功所需的平均查找长度,及查找不成功所需的平均查找长度。
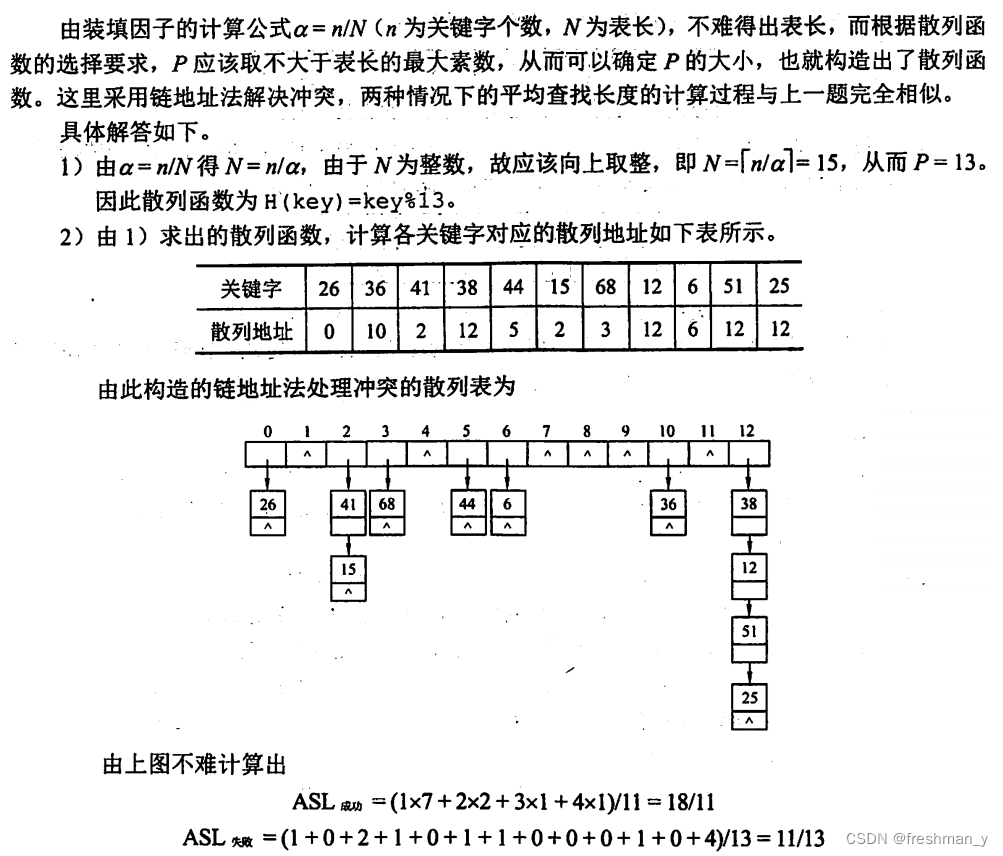
已知一组关键字为{26,36,41,38,44,15,68,12,6,51,25},用链地址法解决冲突,假设装填因子α=0.75,散列函数的形式为H(key)=key%P,回答以下问题:1)构造出散列函数。2)分别计算出等概率情况下查找成功和查找失败的平均查找长度(查找失败的计算中只将与关键字的比较次数计算在内即可)。
设散列表为HT[0...12],即表的大小为m=13。现采用双散列法解决冲突,散列函数和再散列函数分别为:。其中,函数REV(x)表示颠倒十进制数x的各位,如REV(37)=73,REV(7)=7等。若插入的关键码序列为(2,8,31,20,19,18,53,27),请回答:1)画出插入这8个关键码后的散列表。2)计算查找成功的平均查找长度ASL。
8、排序
给出关键字序列{4,5,1,2,6,3}的直接插入排序过程。
给出关键字序列{50,26,38,80,70,90,8,30,40,20}的希尔排序过程(取增量序列为d={5,3,1},排序结果为从小到大排列。
要对{49,27,13,76,97,65,38,49}进行冒泡排序,给出每一趟的排序过程?
冒泡排序思想:从前往后,两两比较,小的往前放。
第一趟排序:27 13 49 76 65 38 49 97
第二趟排序:13 27 49 65 38 49 76 97
第三趟排序:13 27 49 38 49 65 76 97
第四趟排序:13 27 38 49 49 65 76 97
排序结束,最终结果为{13,27,38,49,49,65,76,97}。
要对{49,38,65,97,76,13,27,49}进行快速排序,给出每一趟的排序过程?
要对{2,2,3,5,4,1}简单选择排序,给出每一趟的排序过程?
第一趟:{1,2,3,5,4,2}
第二趟:{1,2,3,5,4,2}
第三趟:{1,2,2,5,4,3}
第四趟:{1,2,2,3,4,5}
第五趟:{1,2,2,3,4,5}
判断序列{11,78,35,62,29,56,48,97,80,35}是否为堆,不是堆请调整为堆。
给出序列{72,87,61,23,94,16,05,58} 小根堆和大根堆排序序列,并分别给出排序过程。
已知序列{503,87,512,61,908,170,897,275,653,462},采用2路归并排序法对该序列做升序时需要几趟排序?给出每一趟的结果。
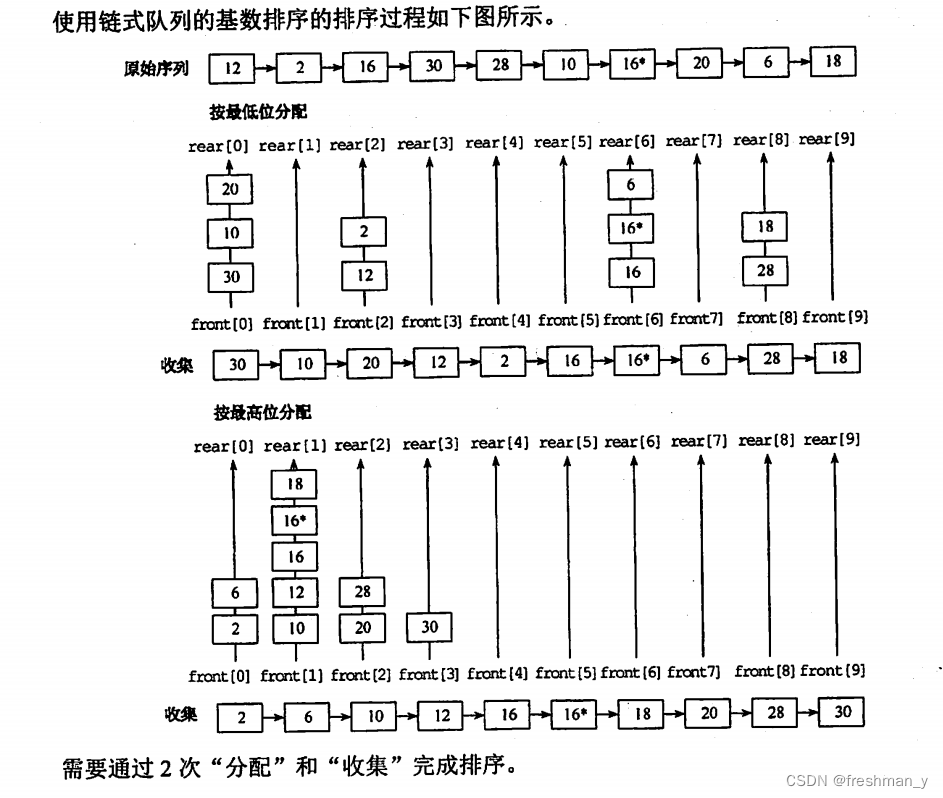
设待排序的排序码序列为{12,2,16,30,28,10,16*,20,6,18},试写出使用基数排序方法每趟排序后的结果,并说明做了多少次排序码的比较。
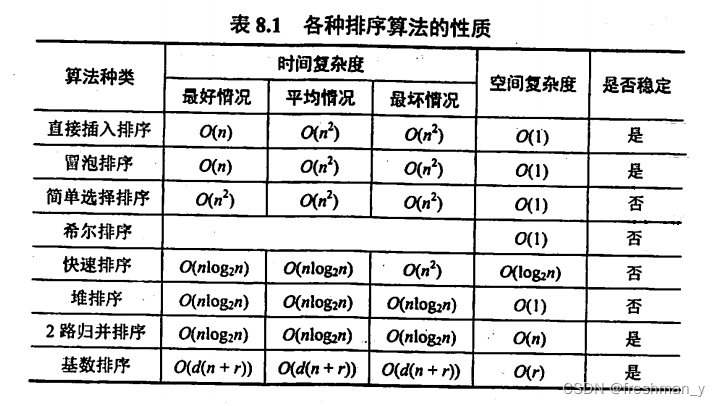
从时间复杂度、空间复杂度、稳定性方面评价各种排序算法?