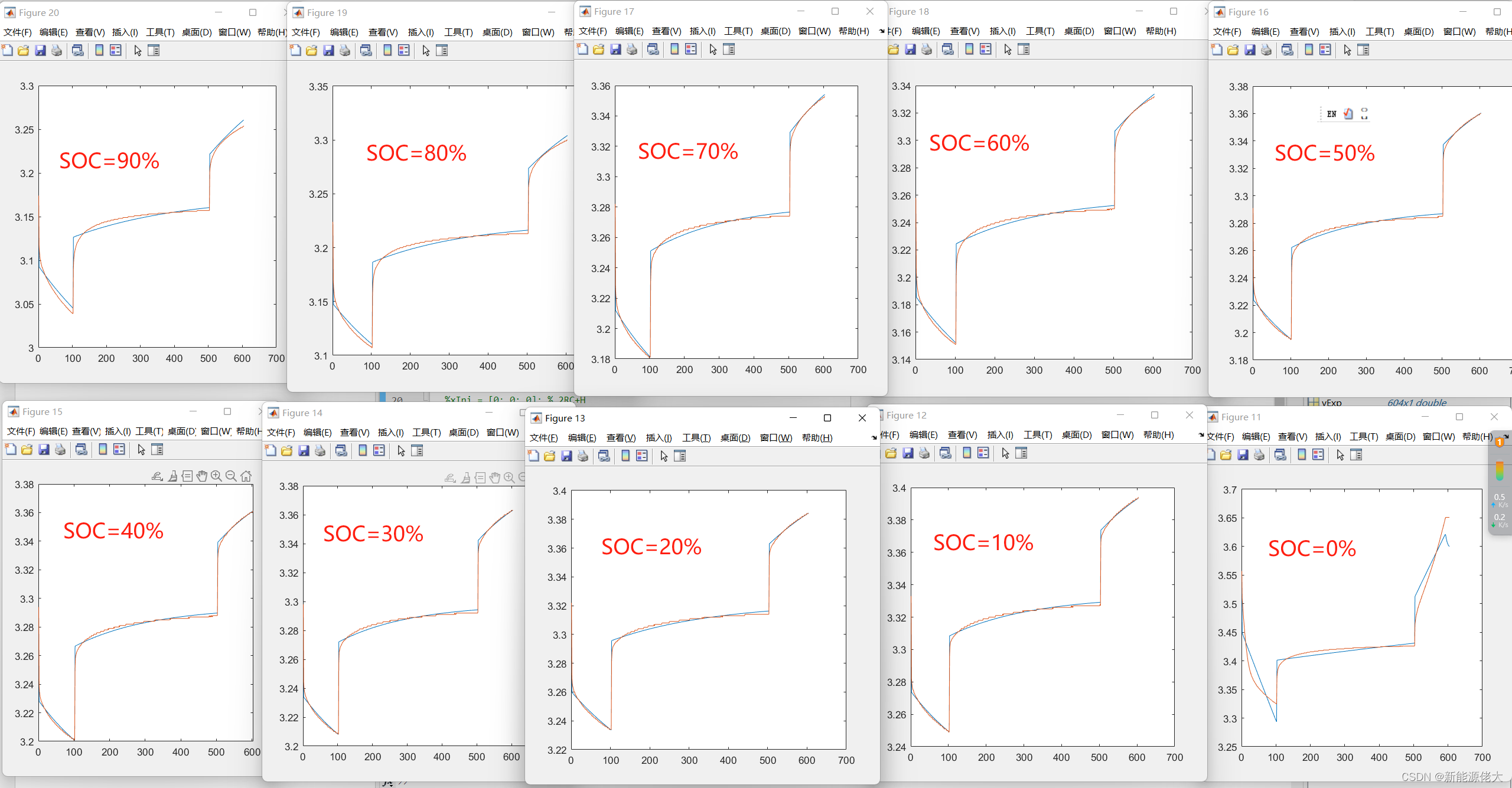
该程序可以离线辨识HPPC工况下的电池数据,只需要批量导入不同SOC所对应的脉冲电流电压数据,就可以瞬间获得SOC为[100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0%]的所有电池参数,迅速得到参数辨识的结果并具有更高的精度,可以很大程度上降低参数辨识的时间,提高参数辨识效率。
1.首先是代码中要更改的参数,我们要根据我们不同的模型选择不同的初始值。
如果是一阶模型iniPar = [0.06;0.03;1000]; 0.06是R0的初始值,0.03是R1的初始值,1000是C1的初始值。
如果是二阶模型iniPar = [0.05;0.05;2000;0.005;800]; 0.05是R0的初始值,0.05是R1的初始值,2000是C1的初始值,0.005是R2的初始值,800是C2的初始值。
如果是1RC+H模型,iniPar = [0.05;0.01;1000;0.001;0.1];
如果是2RC+H模型,iniPar = [0.05;0.01;1500;0.003;200;0.000005;50]
%% 代码中要更改的参数
currentLimit = 10; % 高于此限值的电流将被视为1C电流
iniPar = [0.06;0.03;1000]; % 1RC
%iniPar = [0.05;0.05;2000;0.005;800]; % 2RC
%iniPar = [0.05;0.01;1000;0.001;0.1]; % 1RC+H
%iniPar = [0.05;0.01;1500;0.003;200;0.000005;50]; % 2RC+H2.模型阶数的选择
%% Parameters used in algorithm
xIni = 0; % 1RC
%xIni = [0; 0]; % 2RC and 1RC+H
%xIni = [0; 0; 0]; % 2RC+H
[m,n] = size(dataHPPC{1});
outputPar = zeros(3,n); % %3 - 1RC, 5 - 1RC+H and 2RC, 7 - 2RC+H
modelError = zeros(m,n);
vModel = zeros(m,n);
model = 1; %1 - c1RC, 2 - 2RC, 3 - 1RC+H, 4 - 2RC+H3.运行function函数,求解参数
所有的function函数如下图所示:
二阶RC模型的function函数如下:
function [vModel,XTimUp1,XTimUp2] = Model_2RC (current, tSample, xPrev1,xPrev2, ocvVoltage, ECM_Parameters)
% Model Parameters
r0 = ECM_Parameters(1);
r1 = ECM_Parameters(2);
c1 = ECM_Parameters(3);
r2 = ECM_Parameters(4);
c2 = ECM_Parameters(5);
tau1 = r1*c1;
tau2 = r2*c2;
%% State Time Update
XTimUp1 = exp(-tSample/(tau1))*xPrev1 + r1*(1-exp(-tSample/tau1))*current;
XTimUp2 = exp(-tSample/(tau2))*xPrev2 + r2*(1-exp(-tSample/tau2))*current;
%% The voltage response from the model
vModel = ocvVoltage-XTimUp1-XTimUp2-r0*current;
endfor i = 1:n
time = dataHPPC{1}(:,i);
current = dataHPPC{2}(:,i);
vExp = dataHPPC{3}(:,i);
% Find the ocvCurve value right before the HPPC test starts
index = find(current>currentLimit);
ocvVoltage = vExp(index(1)-0);
% Obtaining the parameter estimates
fun = @(beta,x)ObjectiveFunction(beta,x,ocvVoltage,xIni,model);
outputPar(:,i) = nlinfit([time,current],vExp,fun,iniPar);
% Running the voltage model with the given battery parameters
vModel(:,i) = ObjectiveFunction(outputPar(:,i),[time,current],ocvVoltage,xIni,model);
modelError(:,i) = abs((vModel(:,i) - vExp)./vExp)*100;主要使用了MATLAB的nlinfit函数。
nlinfit函数的用法为:beta = nlinfit(X, Y, modelfun, beta0)
X与Y分别是时间与电压
beta:估计出的非线性函数的系数,即我们辨识的参数值
modelfun:指定的要拟合的非线性函数,即y=a-b*exp(-c*t)-d*exp(-f*t)
beta0:回归系数的初始值,即待辨识参数的初始值。
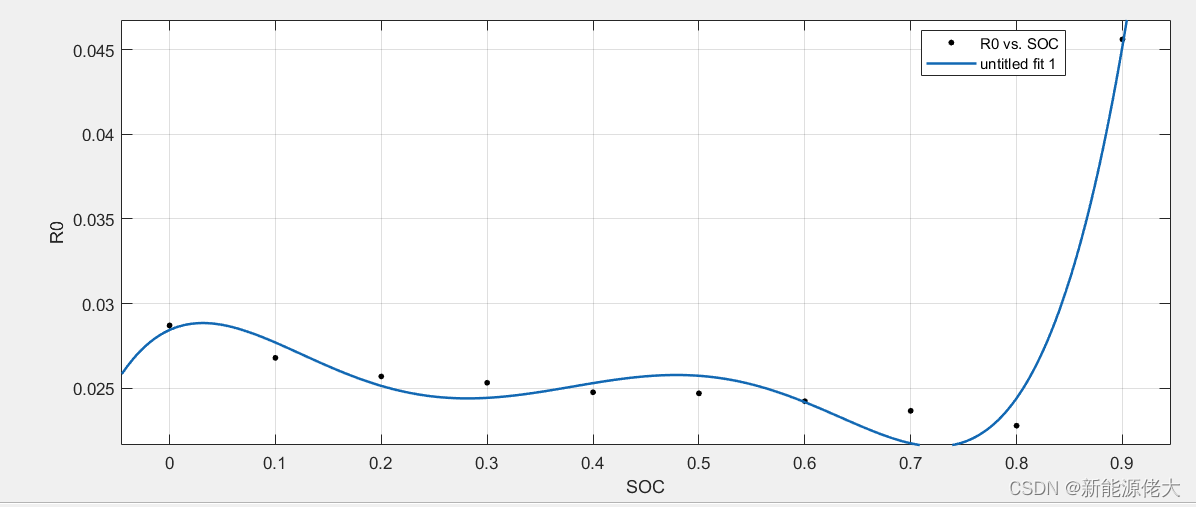
辨识得到的参数结果保存在变量outputPar里面,从左到右依次对应的是不同SOC下所对应的参数,从上到下的五行分别是参数R0、R1、R2、C1、C2。

绘制不同SOC的参数拟合结果如下所示:
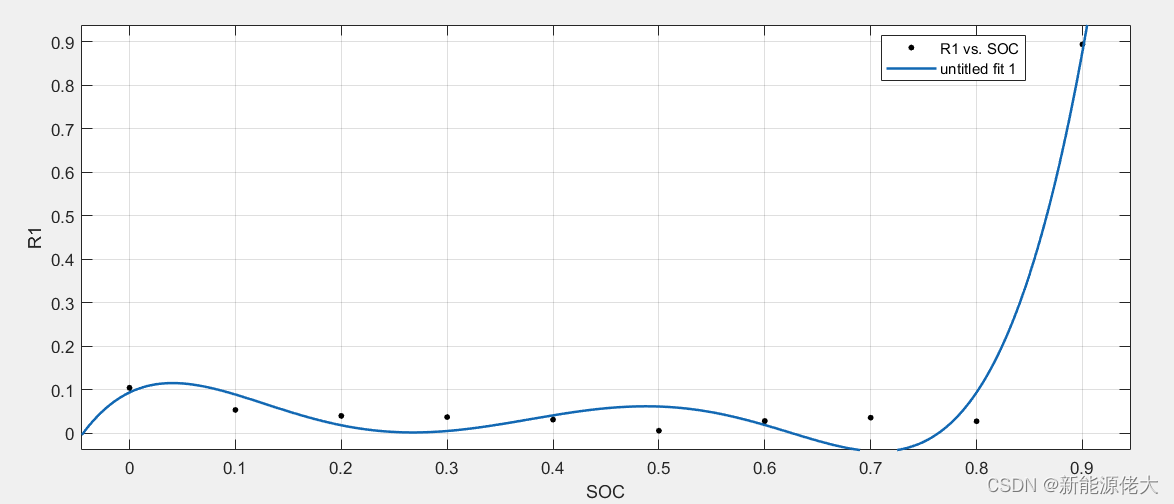
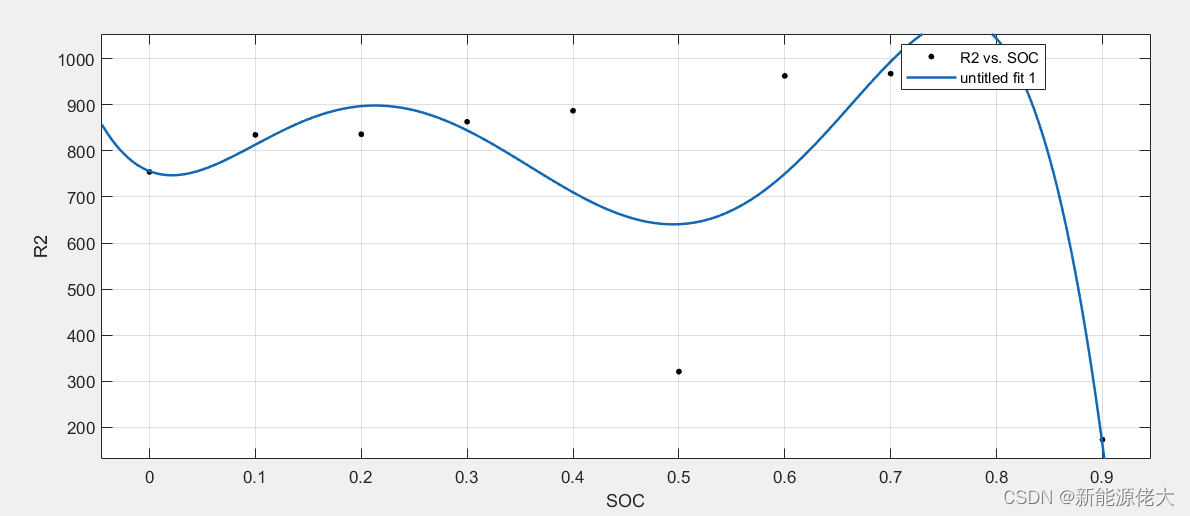
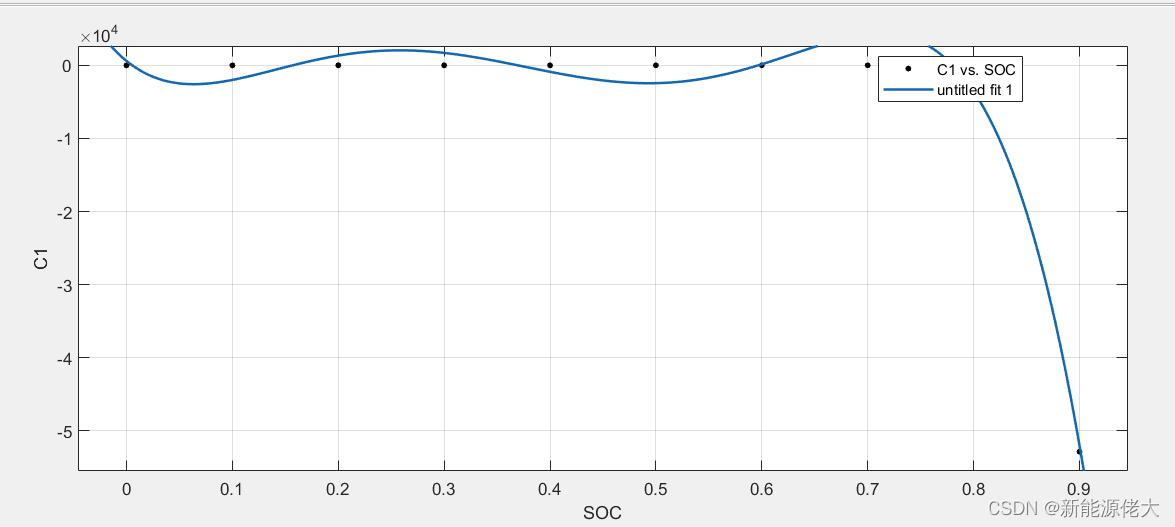
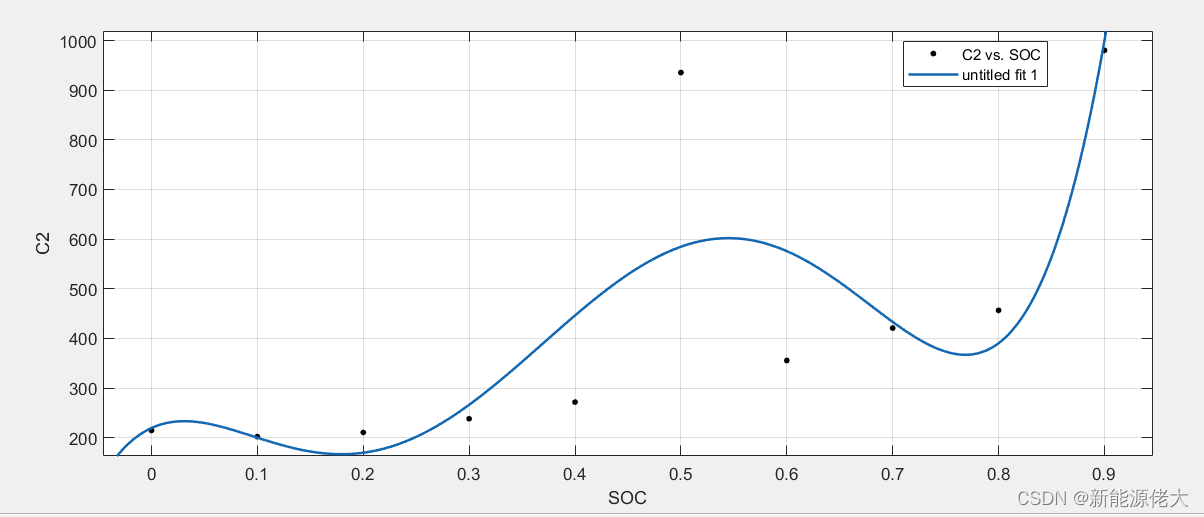
4. 绘图,包括根据辨识的参数值仿真出的端电压与真实测量端电压的对比图、端电压的误差
figure
plot(vModel(:,i))
hold on
plot(vExp)
polt(vModel(:,i)-vExp)
二阶RC模型的端电压拟合情况对比

一阶RC模型的端电压拟合情况对比: