目录
女士品茶
假设检验
样本与总体
原假设与备择假设
检验法、拒绝域与检验统计量
显著性水平
决策方法——临界值法和p值(p-value)法
假设检验步骤
参考文献
假设检验,我们从女士品茶这个故事开始说起。希望这篇文章能给您带来极大的收获。
女士品茶
女士品茶这个故事非常有名,出自于经典的统计学科普读物《女士品茶》。

先让我们穿梭到20世纪20年代末一个夏日的午后。在英国剑桥,一群大学教员、他们的妻子以及一些客人围坐在室外的一张桌子周围喝下午茶。一位叫Muriel Bristol的女士,号称能够分辨出将茶倒进牛奶里和将牛奶倒进茶里的味道是不同的。在座的科学家都觉得这种观点很可笑,没有任何意义。此时,一个又瘦又矮、戴着厚厚的眼镜、留着尖髯的男子表情变得严肃起来,这个问题让他陷入了沉思。这个人就是罗纳德·艾尔默·费歇尔(Ronald Aylmer Fisher)。

当时不到四十岁。他后来被封为罗纳德·费歇尔爵士。Fisher将这位女士和她的观点作为假设检验问题进行了讨论。他考虑了各种实验设计方法,以确定这位女士是否能判断出两种茶的区别。
他首先假设Muriel Bristol女士没有分辨的能力。当然,这位女士可能有这种分辨能力,也有可能没有,这个假设就被称为原假设。之后,Fisher将8杯已经调制好的奶茶随机地放到那位女士的面前,看看这位女士能否正确地分辨出不同的茶。
用字母表示该女士每次答对的概率,用随机变量
表示女士答对的次数;在
次实验中,女士答对
次的概率可以用二项分布来描述:

比如8杯调制好的奶茶实验中,那位女士都答对的概率为:
但是此时,Fisher已经做了假设。这位女士并没有分辨能力。能否答对完全靠蒙,此时,答对的概率,答对答错的概率各一半,类似于抛硬币。此时原假设
:这位女士没有分辨能力,等价于原假设
:这位女士答对的概率
。
利用(1)式二项分布,我们可以计算出,
时女士答对
次的概率,如下图所示:
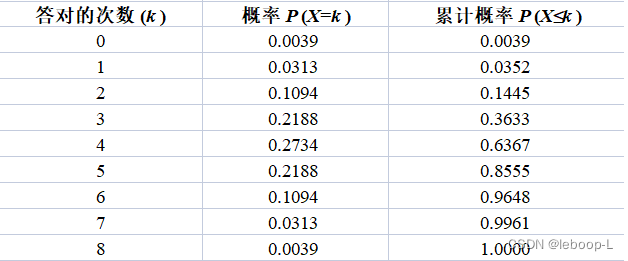
从图中可以看到,这位女士全部答对和全部答错的概率只有0.0039,概率极小,可以认为根本不会发生。但实际情况远远超乎我们的预料。Muriel Bristol女士竟然分辨出全部的奶茶,那么她到底有没有分辨能力呢?也就是从概率的角度来说。原假设到底对不对?

从上面的二项分布累计概率可以看出。如果原假设成立(即女士没有分辨能力),
那么99.61%的情况下,女士蒙对的次数应该。而现在实际观测到的结果是女士连续答对了8次——这说明了什么?当
时,“连续答对8次”的概率比较低,仅为 0.39%;而只有当蒙对的
远远大于0.5 时(比如,接近于1),发生“连续答对8次”这种事情的概率才比较高。也就是说,女士极有可能具备鉴别能力。在一次观测中,当小概率(0.39%)事件发生时,我们有足够的理由怀疑原假设
:
的正确性。
有人可能会问:如果该女士确实没有分辨奶茶的能力,而仅仅是那天运气比较好、连续蒙对了8次。有没有这种可能?当然有这种可能。虽然本例中发生这种情况的概率比较小,仅为0.39%。这就意味着:我们的判断有可能是错误的。如果女士确实没有鉴别能力(原假设为真),而我们根据观测到的样本做出了“拒绝原假设”的错误判断——那我们就犯了一个错误,这个错误在假设检验问题中被称为第一类错误。我们引入第一类错误和第二类错误的概念:
第一类错误(弃真错误):它是指原假设实际上是真的,当通过样本估计总体后,我们拒绝了原假设,犯这个错误的概率记为
,用条件概率表示为 P{拒绝
|
为真}=
。也称为“显著性水平”。
第二类错误(取伪错误):它是指原假设实际上是假的,当通过样本估计总体后,我们接受了原假设,犯这个错误的概率记为
。用条件概率表示为 P{接受
|
为假}=
。
| 假设 | 接受 | 拒绝 |
| 正确 | 第一类错误 | |
| 第二类错误 | 正确 |
回到上面的例子:我们犯第一类错误的概率 α=0.39%。
类似地:如果我们观测到女士答对的次数大于或者等于6次(),我们依然有很大的把握拒绝原假设(因为靠蒙答对6次不大可能)。此时,我们犯第一类错误的概率 α=3.52% (1-96.48%)。
继续这个问题:如果我们观测到女士答对的次数小于或者等于4次(),那么,我们还能拒绝原假设吗?——这时我们会接受原假设,因为靠蒙,我们更相信蒙对的次数不会太高。因此此时如果选择拒绝原假设,我们犯第一类错误的概率α=36.33% (1-63.67%)。相对
或者
的情形,此时,我们犯第一类错误的风险已经增加了很多。
当我们对原假设是否为真作出判断时有可能会犯错误,这就是要冒风险;为了控制这一风险,首先需要用一个概率去表示这一风险的可能性,这个概率便是“原假设为真,但被拒绝”的概率,这个概率又称为显著性水平,记为α,如何控制风险呢?我们要求犯第一类错误的概率不能超过这个显著性水平,即:
P { 拒绝 |
为真 }
为了控制犯第一类错误的概率,一般在假设检验之前就会规定好α的大小。一般规定,或者
。在上面的例子中,如果规定α=0.05,

我们只有观测到时,P { 拒绝
|
为真 }
0.0313+0.0039=0.0352<α才会拒绝原假设(此时犯第一类错误的概率0.0352);如果规定α=0.01,我们只有观测到
时才会拒绝原假设(此时犯第一类错误的概率0.0039)。
假设检验
从字面上来看,假设检验由“假设”和“检验”组成。假设是关于总体某个性质的假设(比如全国成年男性的平均身高,某新型药品是否有效,等等),而检验在样本上完成的。所谓假设检验,就是通过样本来推测总体是否具备某种性质。
上例中,Fisher通过一次实验获得了一个样本;如果他重新再做一次实验,再重新调制8杯奶茶,便会获得另外一个样本。Fisher要推断的总体的性质是:女士是否拥有鉴别“先加奶”还是“先加茶”的能力。
严格来说,所谓假设检验,是指先对总体参数提出某种假设,然后利用样本数据判断假设是否成立。在逻辑上,类似数学中的“反证法”,即先提出假设,再通过适当的统计学方法证明这个假设基本不可能为真。说“基本”,是因为统计得出的结论不是绝对的,是依据概率给出的判定。
假设检验的依据是小概率事件在一次试验中不会发生。
(1)数学中的反证法
例如,对于这样一个数学命题:如果,则
。
我们可以采用“反证法”来证明。假设,因为
,所以得到
,立即得到
,这与条件是矛盾的,于是假设不成立,拒绝假设
,接受
。
数学中“反证法”的拒绝假设是绝对的,无可争议的。而在假设检验中,拒绝假设是基于概率的,依据是小概率事件在一次试验中不会发生。
(2)假设检验中的反正法
例如,某公司生产的100台手机里有5台是次品,所以次品率为5%。但质检团队事先不知道这个信息,于是他们需要通过假设检验来验证。首先,质检团队做如下假设:
次品率不超过5%。
当他们随机抽取一个手机,正好是次品,那么质检团队假设是否正确?
采用“反正法”,假设质检团队的假设正确,即次品率不超过5%,在一次试验中抽取到次品的概率是一个小概率事件,而小概率事件不会发生。这与此次试验中抽取到次品矛盾,所以假设不成立。即次品率超过5%。我们可以看到结果并不一定正确,这也说明假设检验是基于概率的。
样本与总体
总体是指我们所研究的所有元素的集合,其中每个元素称为个体。我们从总体中抽取的一部分个体的集合称为样本,样本中个体的数量称为样本容量。参数是指总体的某个特征,例如总体均值,总体方差等。统计量是指样本的某个特征,例如样本均值,样本方差等。
假设我们通过抽样调查获得一组样本数据,然后据此拟合得到总体某个参数的估计值。那么,我们能否认为总体所对应的参数一定等于0.23呢?不一定。如果我们再次抽样、然后拟合,很有可能得到另一个估计值
。一方面,样本继承了总体的某些性质,我们可以利用样本推断总体的某些性质;另一方面,样本只是总体的一部分,它不等同于总体。样本与总体直接的区别称之为抽样误差(Sampling Error)。由于抽样误差的存在,当我们利用样本推断总体的性质时,总会有犯错的风险。
原假设与备择假设
在一个假设检验问题中常涉及两个相互排斥的假设。所要检验的假设为原假设,或零假设,记为。与
相反的假设称为备择假设,记为
。原假设一般是统计者想要拒绝的假设,而备则假设是统计者想要接受的假设。例如Fisher实验中,原假设
:该女士没有分辨奶茶的能力,这个假设是Fisher要拒绝的假设。
这里有个有趣的问题值得我们思考。为什么把要拒绝的假设作为原假设呢?在假设检验中,我们对原假设是比较宽容的:如果样本中的证据不够充分,我们会选择接受原假设。只有当样本中出现了足够强的证据时,我们才会推翻/拒绝原假设。此时,当我们选择拒绝原假设时,只会犯第一类错误:
假设 接受 拒绝 为真
正确 第一类错误 为假
第二类错误 正确
而犯第一类错误的概率是受我们事先选定好的显著性水平的控制的,即
P { 拒绝
|
为真 }
而且这个风险的概率一般很小。
检验法、拒绝域与检验统计量
样本中提供了一定的信息(证据),可以用于判断原假设是否成立。为了方便判断,一般需要对这些证据进行加工处理,计算得到一个统计量,然后将该统计量与事先选好的阈值进行对比。这个综合了样本信息的统计量被称为检验统计量。
我们看另外一个例子。
某车间用一台包装机包装葡萄糖。已知每袋糖的净重是一个随机变量
,且服从标准差为 15 g 的正态分布。某一天随机抽取该包装机所包装的9袋糖,称得净重为(g):
497,506,518,524,498,511,520,515,512
问每袋糖的净重的均值
是否为500g?
在本检验问题中,相应的原假设和备择假设
分别为:
由于这里涉及的是总体均值的假设检验,故首先想到的是能否借助样本中提供的信息,进行加工计算来进行判断,加工计算应该和样本的均值相关。
样本中包含了糖的净重的9个观测值;我们并不会直接用这9个观测值中任何一个值去判断原假设是否成立,因为这样会丢失掉其他8个观测值所包含的信息,导致判断的结果准确性就很低。我们需要综合所有9个样本的信息,我们想到的是使用样本的均值
。这是因为,样本均值
是总体均值
的无偏估计,这样的话,样本
的观测值
一定程度上反应了总体均值
的大小。
什么是无偏估计呢?上面我们说过。对于一个总体,抽取的样本并不是唯一的。上面9个观察值只是某一天的观测到的值,只是其中一个样本,对应的样本均值可能比实际的总体均值小,如果换一天,我们再观测9个值,就能得到另外一个样本,新的样本的样本均值
,可能比实际的总体均值大。依次类推,我们其实能得到很多这样的样本均值,这些样本均值有的比总体均值
大,有的比总体均值小,但是他们的均值仍然是u,这就是所谓的无偏估计。如果
为真,则观察值
与
的偏差一般不应太大。若偏差过大,我们就有理由怀疑原假设
的正确性,从而拒绝
。
现在我们构造什么样的统计量呢?别忘了,我们假设成立。构造如下统计量
为啥要构造这个统计量呢?因为,是我们再熟悉不过的标准正态分布。
本例中,,即
化简后
是本例的检验统计量。
现在已经有了检验统计量,而且该统计量的分布也是已知的,即
。下面如何检验呢?也就是我们的判断标准是什么。我们回到
与500的偏差上来。假设我们选择了一个阈值k(注意:这里
不是显著性水平
)。
当
时,说明两者偏差较大,原假设不成立,我们拒绝
,
当
时,说明两者偏差不大,原假设成立,我们接受
。

上图是的分布函数,也就是标准正态分布,横轴是
。
时,我们拒绝原假设
,这里z的取值集合我们称之为拒绝域。也就是在图中灰色部分是我们拒绝原假设的区域,中间部分是我们接受原假设的区域。
我们对上面情况,做如下一般地描述:
在一个假设检验问题中,所谓检验法则(简称检验法)就是设法把样本空间
划分为互不相交的两个集合
,并作如下规定:
(1)当观测值时,就拒绝原假设
,认为备择假设
成立;
(2)当观测值时(即
),就不拒绝原假设
,认为原假设成立。
这里的称为检验的拒绝域。这样一来,选定了检验法,就是确定了拒绝域;反之,选定了拒绝域,也就确定了检验法。
显著性水平
上面我们已经构造好了一个统计量,并给出了拒绝域的形式。但是如何确定拒绝域中k的取值呢?上面我们说了,值不是显著性水平
,那它和显著性水平
有什么样的关系呢?
从女士品茶的例子中可以看到,k的取值是由控制犯第一类错误的概率决定的。若设定
,我们只有观测到“女士答对7次或者7次以上”时,才会拒绝原假设;若设定
,则只有当观测到“女士答对8次”时才会拒绝原假设。
可见,如果我们希望犯第一类错误的概率越小(即越小),拒绝域的面积越小,对证据的要求就越高,
值越大。从z的标准正态分布上也可以看出,拒绝域的面积越小,k值向z轴两边扩大。如下图所示:
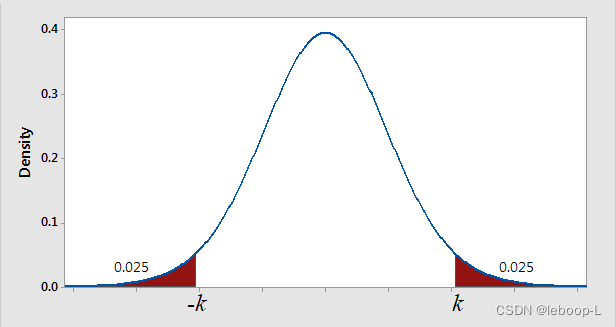
上图表示,红褐色两边面积各为
。
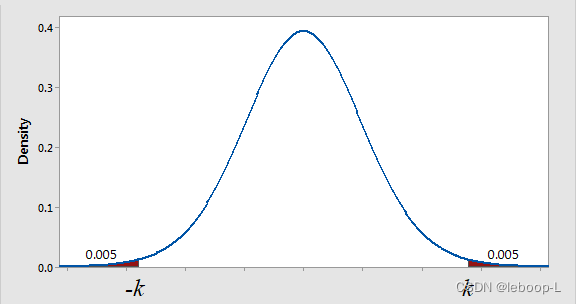
上图表示,红褐色两边面积各为
。
按照第一类错误中显著性水平的定义:
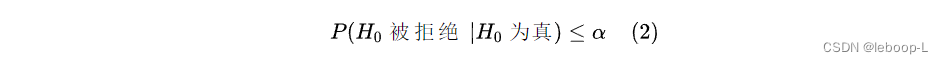
由前文知到,“被拒绝”这一事件等价于;于是,(2)式的左边等价于:,于是(2)式的左边等价于:
P { 被拒绝 |
为真}
(3)
于是
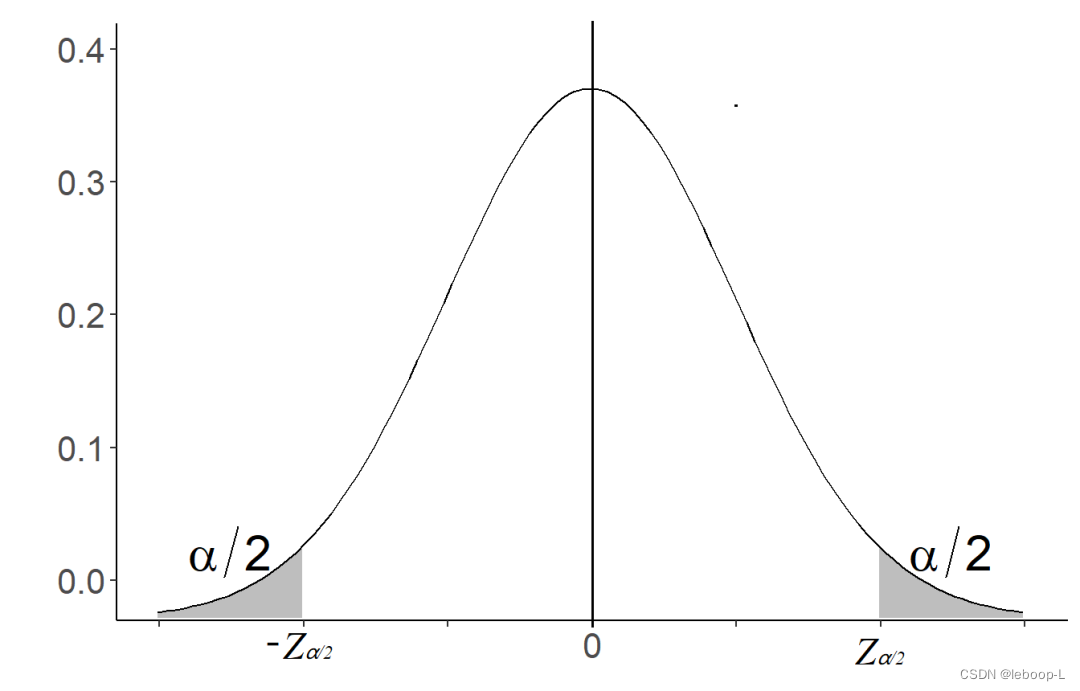
看上面的这个正态分布函数图像,得到:
即k最小取,此时,我们已经找到了k值与显著性水平
的关系。
因此若检验统计量,则拒绝原假设,若
,则接受原假设。
如果,
,
如果,
。
这里k的值是查找标准正态分布表所得。到这里我们已经找到了k的值。
又被称为
统计量;以上这种利用
统计量进行检验的方法称为
检验法。
决策方法——临界值法和p值(p-value)法
给定显著性水平,我们便可以确定拒绝域
的范围,如下图所示。

灰色部分即为拒绝域。也就是满足的样本,即拒绝域为
若检验统计量的值落入拒绝域,便可拒绝原假设。下面我们来计算一下,
,
相应检验统计量的值
,
说明例子的样本综合计算出的检验统计量的值落在拒绝域内,最终我们会拒绝原假设。也就是说每袋糖的净重的均值
不是500g。这个方法被称为
临界值法。
p值同样可以用于判断是否拒绝原假设。什么是p值呢?
p值指的是当原假设为真时,比所得到的样本观察结果更极端的结果出现的概率。如下图所示:
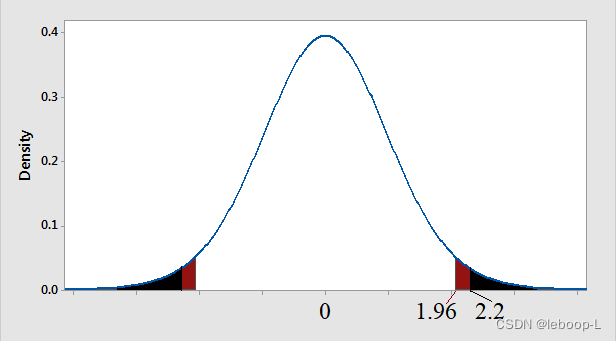
在本例中,所得到的样本观察结果是检验统计量的值为2.2。比这个结果更极端,也就是满足如下条件的样本观察结果比2.2更极端
它对应的概率即为p值,如下:
如上图黑色部分所示。
如果p值很小,说明原假设情况的发生的概率很小,而如果出现了,根据小概率事件原理,我们就有理由拒绝原假设,p值越小,我们拒绝原假设的理由越充分。总之,p值越小,表明结果越显著。但是检验的结果究竟是“显著的”、“中度显著的”还是“高度显著的”需要我们自己根据p值的大小和实际问题来解决。
假设检验步骤
总结一下假设检验的几个步骤:
(1)提出原假设,确定业务需求。
(2)选择合适的检验统计量。
(3)确定显著性水平。
(4)计算检验统计量
(5)做出统计决策,接受或拒绝原假设。
现在读者可以尝试使用该步骤,一步步来检验品茶的女士到底有没有鉴别奶茶的能力?
参考文献
假设检验——这一篇文章就够了
假设检验(hypothesis testing)_yanrong_01的博客-CSDN博客
假设检验(Hypothesis Testing)