2014年亚太杯APMCM数学建模大赛
C题 公共基础课教师专业化培养方式研究
原题再现
近年来,世界基础工业、信息产业、服务业的跨越式发展引发了大量人才需求,导致了职业教育的飞速发展,除原有专科层次高等职业教育院校外,大量普通本科院校逐渐开始向本科层次的高等职业教育转型。
职业教育的落脚点是依靠专业进行就业,公共基础课同样也有为专业服务的职能。公共基础课作为高校培养学生文化素质和综合职业能力的课程,也需要有高素质专业化(含基础与专业结合)的教师,高校公共基础课教师的专业化发展也因此提上议事日程。
职业教育推崇淡化公共基础课教师和专业课教师的界限, 逐步实现教师一专多能。要达到这一目标,可以通过调研高校公共基础课教师队伍建设现状、存在的问题及其原因,论证公共基础课教师专业化发展的内涵、必要性,并从高校层面和教师层面为公共基础课教师队伍专业化培养提出可行性操作策略,探讨高校如何根据教育目标及自身实际条件搭建公共基础课师资培养平台,促进高校高素质教师队伍建设,提高高校教育教学质量。现有问题如下:
(1)某高校部门与学科设置如下:
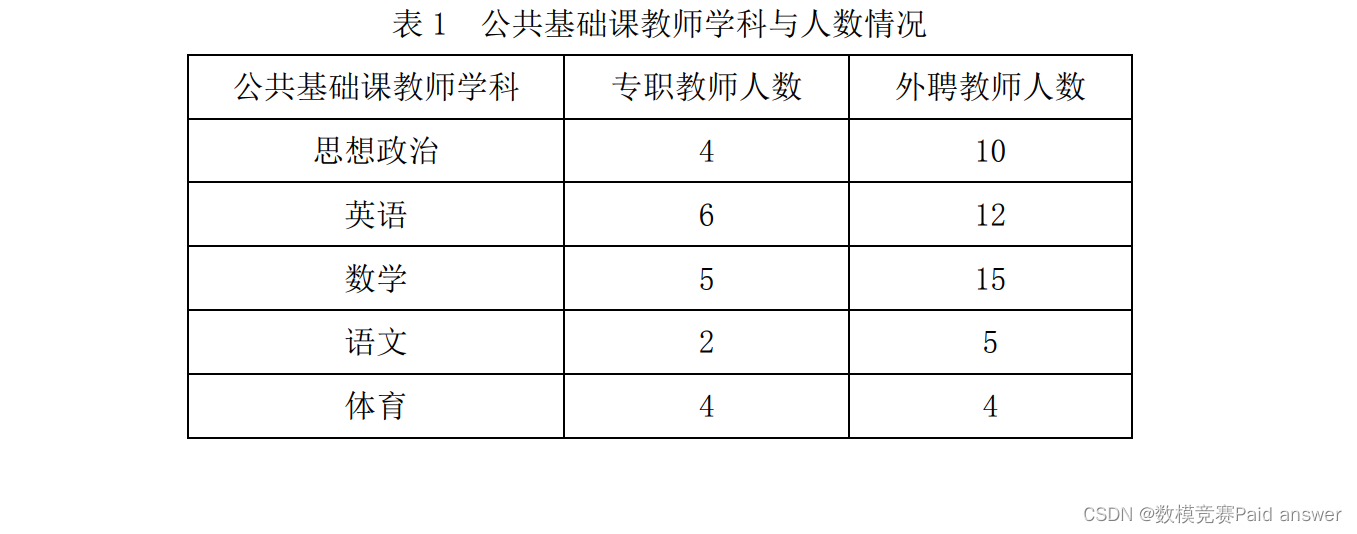
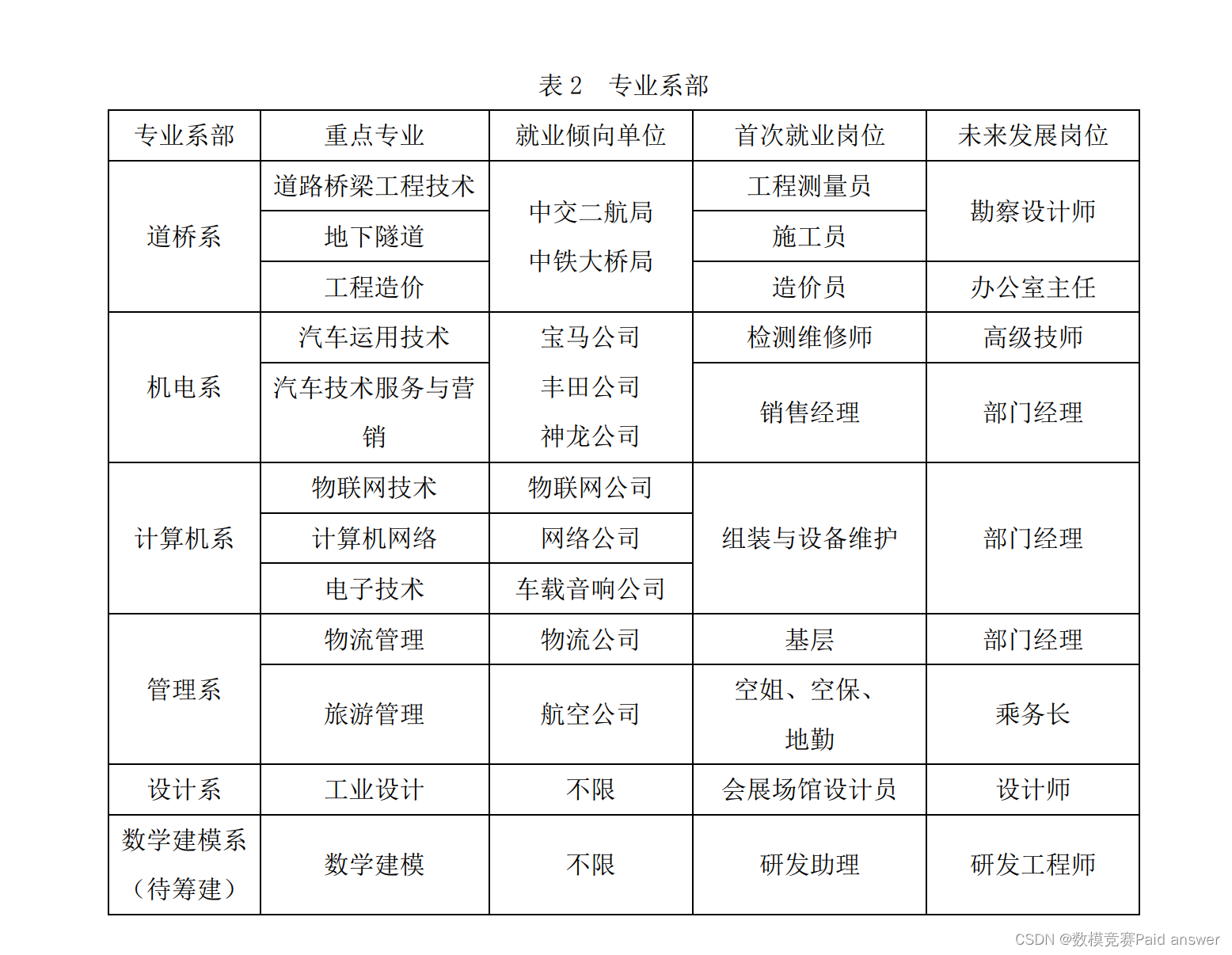
其中,数学专职教师已经有比较固定的专业系部教学分配(其中道桥系 2 人、计算机系 2 人、管理系 1 人),现将所有公共基础课教师(含外聘)全部安排至专业系部进行针对各系的学生教学与教师专业化培养,需要考虑教师(尤其是专职教师)对于全校系部的覆盖面、学生学习基础课和专业课对于就业和发展的贴近度,请结合以上数据提出公共基础课教师分配到专业系部的合理化分配方案。
(2)现需调查高校公共基础课教师队伍现状(师资结构、职业能力、专业化水平、培养与培训情况、职业倦怠等)以及高校对公共基础课教师职业能力的要求及构成。请设计一份调查问卷,并给出保证问卷的内容全面科学、调查真实可靠、统计结果分析有力的方法。
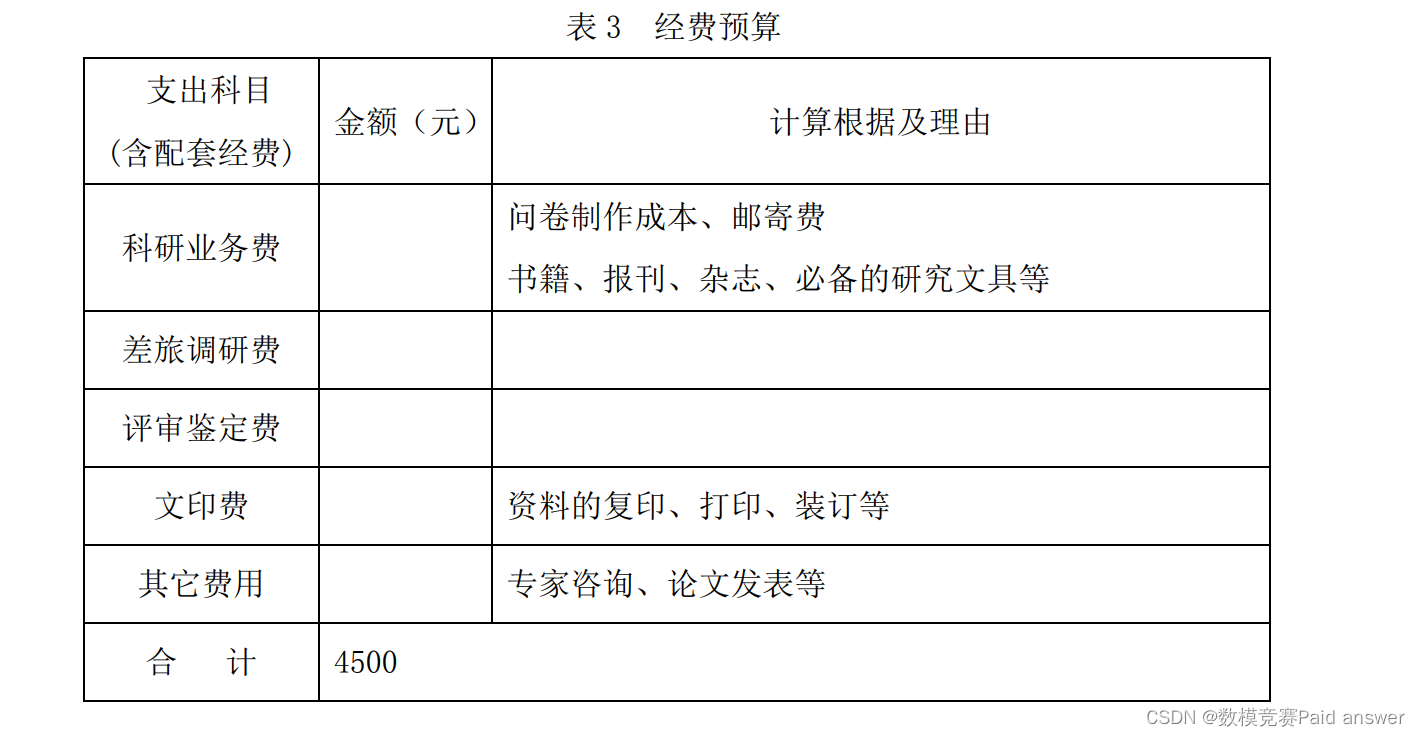
(3)现共安排 1 年时间(含前期、中期、尾期)、经费 4500 元完成以上工作,请设计一个研究进程计划和对应的经费预算方案,合理安排经费的使用(分前期、中期、尾期),参考如下表 3:
(4)请为相关教育管理部门提供一份公共基础课教师队伍专业化培养可行性依据、操作策略及合理化建议(报告),分析高校公共基础课教师专业化发展的内涵、必要性,为提高公共基础课教师的职业能力和实现公共基础课既提高学生综合素质又为专业服务的双重目标探索出可行性高、实施效果好、可持续发展的模式和方法,为高校公共基础课教学改革、公共基础课师资队伍建设提供科学的论证和实践依据。
整体求解过程概述(摘要)
近年来,对教师专业发展的研究主要集中在“双师”培养上。但随着职业教育的快速发展,研究相对较少的公立大学教师专业发展课程也被提上了议事日程。基础课程作为学生综合专业能力的课程,也需要有高水平的专业教师。因此,有必要对公共基础课教师的专业成长进行研究,分析新的培训模式和基础课教师队伍的现状,以解释基础课教师专业成长策略。
对于第一个问题,我们分析了数据,并将获得教师和专业方法学位的部门的覆盖率作为第一、第二个目标函数,其中包括覆盖部门的部门总数和偏差分布。以教师数量为约束条件,建立公共基础课教师专业化配置模型。然后考虑到全职教师和外部教师的差异,根据不同的目标,我们设置了不同的权重来校正模型。使用MATLAB软件,根据优先级,首先,我们求解出最大专业接近度为197.8,然后调整第二个目标函数作为约束条件,使用LINGO软件求解,得到教师的最优分配方案,部门覆盖和分布的偏差总数为5.90.0251,专业接近度达到183.5。
对于第二个问题,分析可以反映公共基础课教师现状的几个具有代表性的指标:教师结构和教师的专业能力、专业水平、培训和培训情况以及工作倦怠。在深入分析的基础上,专门设计了每个指标来调查评分问题,然后每个部分都可以得到总分,并建立了教师公共基础课程的评估模型和评分。然后我们进行了一项调查,结果为一流大学0.831分,这与事实相一致,证明了问卷的可靠性。对于大学教师专业能力公共基础课程要求的调查,我们通过专业能力问卷进行调查,问题层次多样,能够充分反映对教师和作文的要求。
对于第三个问题,我们结合实际生活和问题分析,考虑时间和金钱的限制,设计出合理详细的计划,然后根据市场价格制定出经济可靠的预算计划。
针对第四个问题,我们分析了大学公共基础课教师专业发展的意义和必要性,提出了一种淡化公共学科体系、将基础教学体系和实践体系与专业课程联系起来、改变传统教学观念的方法。从教师、高校和学生三个层面分析了公共基础课教学,提出了提高公共基础课教师专业能力、提高学生综合素质的方法,为公共基础课的教学改革和师资队伍建设提供了现实依据。
最后,对本文提出的模型进行了分析、评价和推广。
模型假设:
准确性假设:我们假设问题给出的数据是准确可信的。
理想假设:我们假设教师完全服从分配,不受外部因素的影响。
排他性假设:不考虑其他公立小学教师和其他部门的分配。
问题分析:
问题分析1
公立小学教师的合理分配问题1。我们考虑了以下因素:获得教师的部门(尤其是全职教师)的覆盖范围,分配到一个部门的教师的公共基础课程(PEC)是否与该部门学生所从事的工作接近。
问题分析2
为了调查PEC教师队伍的现状(教师结构、职业能力、专业化水平、培养与培训、职业倦怠等),并考虑到高校对教师职业能力的要求,我们需要设计一份全面、可靠、令人信服的问卷。
问题分析3
我们需要制定一个研究计划和相应的拨款预算(总时间:一年,总资金:4500元)。该计划包括三个阶段:前期、中期和后期。主要任务是准备、实际检查和结果分析,分为三个阶段。
问题分析4
PEC专业教师的专业培训是通过专业培训学习教学技能,实现职业自主,体现职业道德,提高教学质量,成为教学生活中的专业教育工作者。其内涵包括职业精神、职业道德、职业智慧、职业自主和职业组织。能力包括综合能力、专业学术能力、专业行为能力、教育研究能力和自我发展能力。
模型的建立与求解整体论文缩略图


全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
部分程序如下:
model:
sets:
e/1..6/:a1,a2,k;
f/1..5/:n1,n2;
assign(e,f):c,b1,b2;
endsets
data:
n1=4 6 5 2 4;
n2=10 12 15 5 4;
k=3 2 3 2 1 1;
c=5 6 8 1 6
4 5 4 1 3
3 8 6 2 1
6 7 7 3 3
5 4 5 4 5
3 7 9 3 4;
rmp1=0.9; !Parameter
assignment
ita1=0.7;
enddata
b1(1,3)=2;b1(3,3)=2;b1(4,3)=1;
rmp2=1-rmp1;
ita2=1-ita1;
kz=@sum(e(i):k(i));
nz1=@sum(f(j):n1(j));
nz2=@sum(f(j):n2(j));
@for(e(i):a1(i)=@SMIN(1,@sum(f(j):b1(i,j))));
@for(e(i):a2(i)=@SMIN(1,@sum(f(j):b2(i,j))));
max=@sum(e(i):rmp1*a1(i)+rmp2*a2(i))-@sqrt(@sum(e(i):(rmp1*(@sum(f(j):
b1(i,j))/nz1-k(i)/kz))^2+(rmp2*(@sum(f(j):b2(i,j))/nz2-k(i)/kz))^2)/5);
!min=@sqrt(@sum(e(i):(rmp1*(@sum(f(j):b1(i,j))/nz1-k(i)/kz))^2+(rmp2*(@su
m(f(j):b2(i,j))/nz2-k(i)/kz))^2)/5); !Directly solve Sub-objective
function
!@sum(assign:ita1*c*b1+ita2*c*b2)>185; !Constraints in
program 3
@sum(e(i):b1(i,1))-4<1e-3;
@sum(e(i):b1(i,1))-4>-1e-3;
@sum(e(i):b1(i,2))-6<1e-3;
@sum(e(i):b1(i,2))-6>-1e-3;
@sum(e(i):b1(i,3))-5<1e-3;
@sum(e(i):b1(i,4))-2<1e-3;
@sum(e(i):b1(i,4))-2>-1e-3;
@sum(e(i):b1(i,5))-4<1e-3;
@sum(e(i):b1(i,5))-4>-1e-3;
@sum(e(i):b2(i,1))-10<1e-3;
@sum(e(i):b2(i,1))-10>-1e-3;
@sum(e(i):b2(i,2))-12<1e-3;
@sum(e(i):b2(i,2))-12>-1e-3;
@sum(e(i):b2(i,3))-15<1e-3;
@sum(e(i):b2(i,3))-15>-1e-3;
@sum(e(i):b2(i,4))-5<1e-3;
@sum(e(i):b2(i,4))-5>-1e-3;
@sum(e(i):b2(i,5))-4<1e-3;
@sum(e(i):b2(i,5))-4>-1e-3;
@for(e(i):a1(i)-1<1e-3);
@for(e(i):a2(i)-1<1e-3);
@for(e(i):@BIN(a1(i)));
@for(e(i):@BIN(a2(i)));
@for(assign(i,j):@GIN(b1(i,j)));
@for(assign(i,j):@GIN(b2(i,j)));
end
model:
sets:
e/1..6/:a1,a2,k;
f/1..5/:n1,n2;
assign(e,f):c,b1,b2;
endsets
data:
n1=4 6 5 2 4;
n2=10 12 15 5 4;
k=3 2 3 2 1 1;
c=5 6 8 1 6
4 5 4 1 3
3 8 6 2 1
6 7 7 3 3
5 4 5 4 5
3 7 9 3 4;
rmp1=0.9; !Parameter
assignment
ita1=0.7;
enddata
b1(1,3)=2;b1(3,3)=2;b1(4,3)=1;
rmp2=1-rmp1;
ita2=1-ita1;
kz=@sum(e(i):k(i));
nz1=@sum(f(j):n1(j));
nz2=@sum(f(j):n2(j));
@for(e(i):a1(i)=@SMIN(1,@sum(f(j):b1(i,j))));
@for(e(i):a2(i)=@SMIN(1,@sum(f(j):b2(i,j))));
max=@sum(assign:ita1*c*b1+ita2*c*b2);
@sum(e(i):b1(i,1))-4<1e-3;
@sum(e(i):b1(i,1))-4>-1e-3;
@sum(e(i):b1(i,2))-6<1e-3;
@sum(e(i):b1(i,2))-6>-1e-3;
@sum(e(i):b1(i,3))-5<1e-3;
@sum(e(i):b1(i,4))-2<1e-3;
@sum(e(i):b1(i,4))-2>-1e-3;
@sum(e(i):b1(i,5))-4<1e-3;
@sum(e(i):b1(i,5))-4>-1e-3;
@sum(e(i):b2(i,1))-10<1e-3;
@sum(e(i):b2(i,1))-10>-1e-3;
@sum(e(i):b2(i,2))-12<1e-3;
@sum(e(i):b2(i,2))-12>-1e-3;
@sum(e(i):b2(i,3))-15<1e-3;
@sum(e(i):b2(i,3))-15>-1e-3;
@sum(e(i):b2(i,4))-5<1e-3;
@sum(e(i):b2(i,4))-5>-1e-3;
@sum(e(i):b2(i,5))-4<1e-3;
@sum(e(i):b2(i,5))-4>-1e-3;
@for(e(i):a1(i)=1);
@for(e(i):a2(i)=1);
@for(e(i):@BIN(a1(i)));
@for(e(i):@BIN(a2(i)));
@for(assign(i,j):@GIN(b1(i,j)));
@for(assign(i,j):@GIN(b2(i,j)));
end