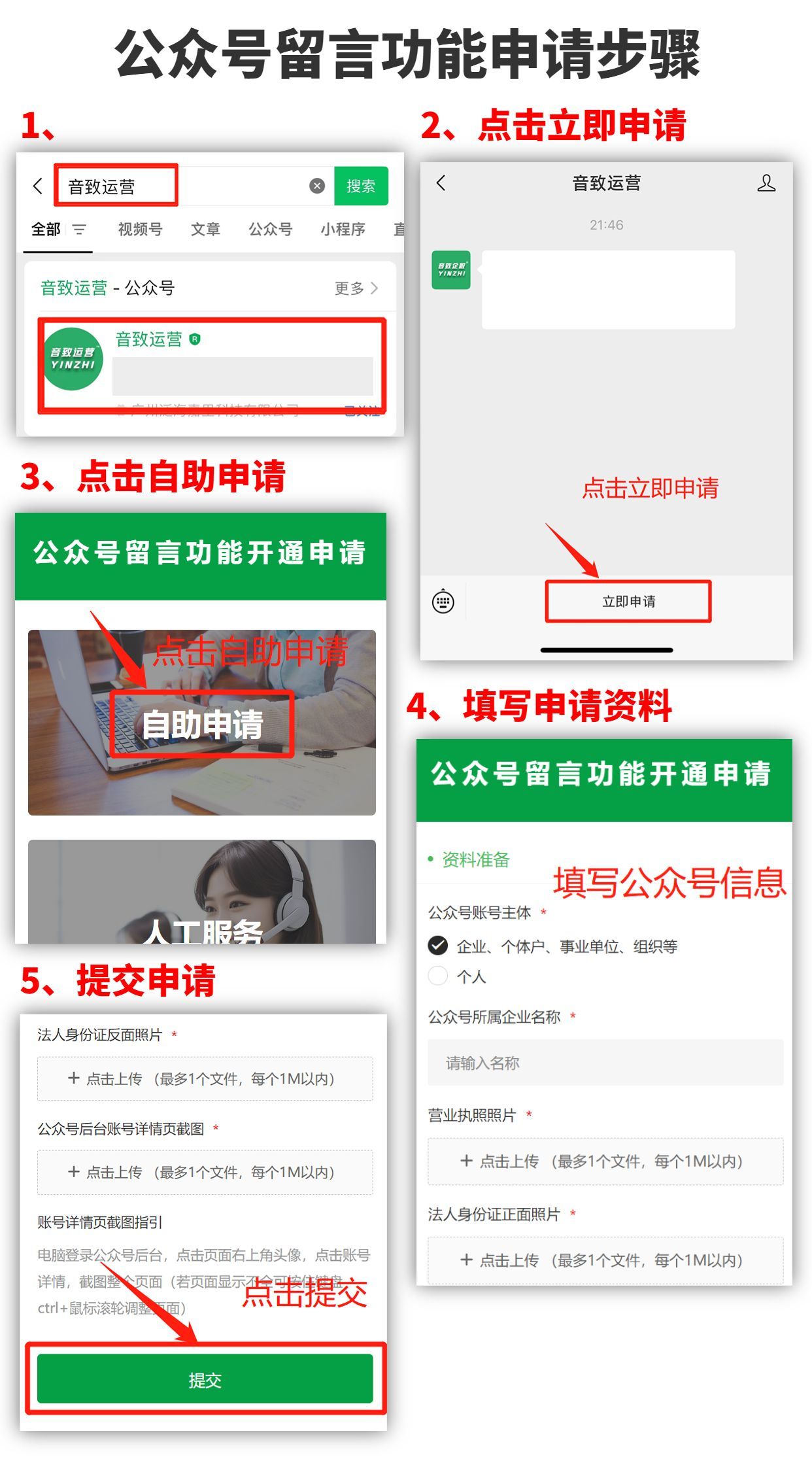
[python 刷题] 1248 Count Number of Nice Subarrays
题目如下:
Given an array of integers
numsand an integerk. A continuous subarray is called nice if there arekodd numbers on it.Return the number of nice sub-arrays.
这道题和 1343 Number of Sub-arrays of Size K and Average Greater than or Equal to Threshold 挺像的
双指针
先声明,我的写法不是最有效的,其他的双指针/滑动窗口的解法会更加的高效,不过我感觉对我来说这么写是最好理解的
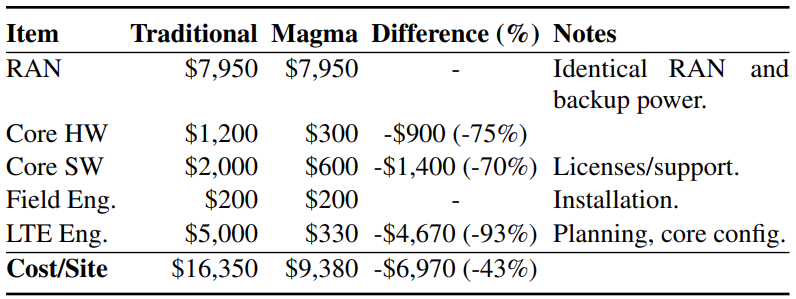
首先题目要求必须要有 k 个奇数,以题目中 Input: nums = [2,2,2,1,2,2,1,2,2,2], k = 2 为例,它的 base case 是这样的:

同时,因为两边都是偶数,因此指针是可以向两边延长的,演唱后也都是满足题目需求,即,子数组中有 k 个奇数
首先用两个指针指向 l l l 和 r r r,使用 c o u n t e r counter counter 计算 [ l , l + 1 , . . . , r ] [l, l + 1, ..., r] [l,l+1,...,r] 中的奇数。每次移动 r r r 的时候,更新 c o u n t e r counter counter,这时候会出现两个需要照顾的条件:
-
c o u n t e r > k counter > k counter>k
这个时候就需要不断移动 l l l,一直到 c o u n t e r = = k counter == k counter==k
-
c o u n t e r = = k counter == k counter==k
依旧以上面的案例来说,因为左侧指针没有动过,实际上应该是这样的情况:

这时候新建一个 t e m p temp temp 指针代替右侧指针,并且将 d i f f diff diff 保存下来:

这里的 d i f f diff diff 代表着不同的组合,即 l l l 移动一格时所会产生的不同组合,在移动左侧指针时,每次添加 d i f f diff diff 即可
代码如下:
class Solution:
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
n = len(nums)
res, count = 0, 0
l, r = 0, 0
while r < n:
if nums[r] % 2:
count += 1
while count > k:
if nums[l] % 2:
count -= 1
l += 1
if count == k:
res += 1
t = r + 1
while t < n and not nums[t] % 2:
res += 1
t += 1
diff = t - r
r = t - 1
while l < r and not nums[l] % 2:
res += diff
l += 1
r += 1
return res
prefix sum
使用 prefix sum 就比较简单了,这里是将所有出现奇数的次数全都保存下来到一个变量中,同时,会形成一个 {odd_num: even_num_freq + 1} 的对应关系,这样可以保存不同的组合
如 Input: nums = [2,2,2,1,2,2,1,2,2,2], k = 2,它的键值对的关系为 {0: 4, 1: 3, 2: 4},其中保存的对应关系为:
0: [default_value, 2,2,2]
1: [1,2,2]
2: [1,2,2,2]
这样,通过 count[odd_count - k] 就能够获取对应的变化,也就是上一个解法中的
d
i
f
f
diff
diff,代码如下:
class Solution:
def numberOfSubarrays(self, nums: List[int], k: int) -> int:
n = len(nums)
# 这里使用数组而非字典,不过其原理是一样的
# 使用 n + 1 是因为 0 为没有出现 odd 的情况
# 而当数组中所有的成员都是 odd 时,count 的长度就为 n + 1
count = [0] * (n + 1)
# 这个是 base case
# 空数组也是一个合法的 subarray
count[0] = 1
odd_count = 0
res = 0
for num in nums:
if num % 2 == 1:
odd_count += 1
if odd_count >= k:
res += count[odd_count - k]
count[odd_count] += 1
return res