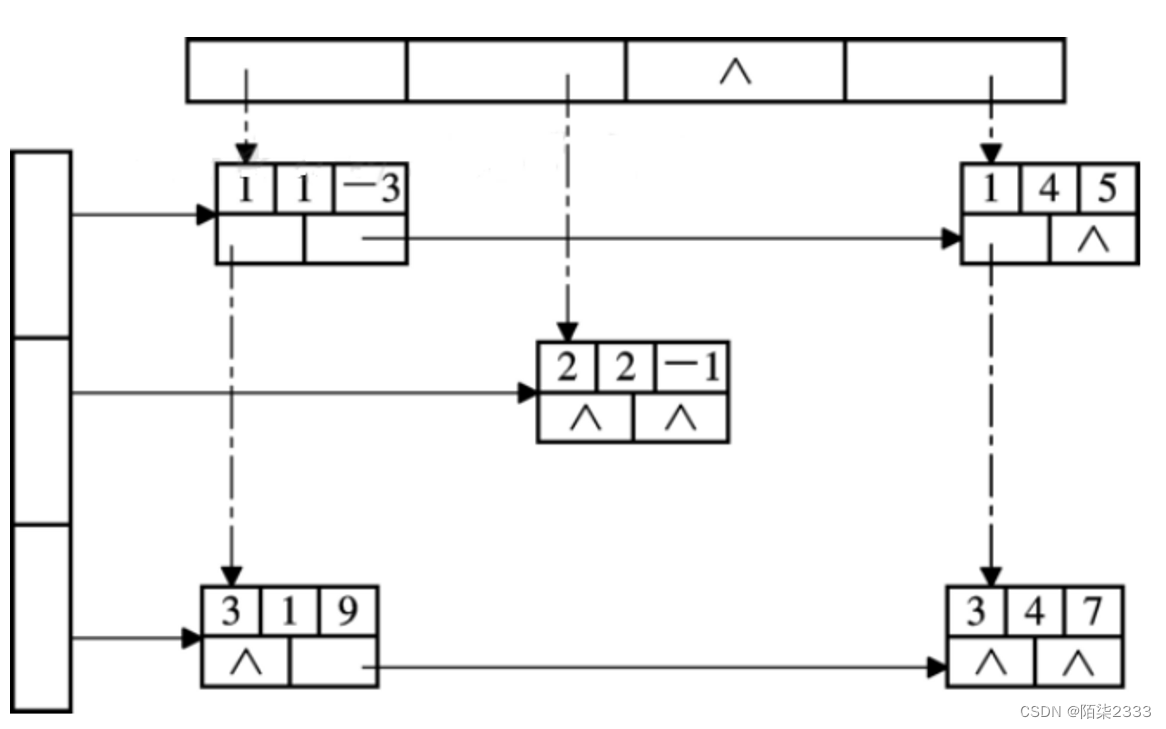
广义表

广义表（又称Lists）是n>=n个元素a0,a1,…,an-1的有限序列，其中每一个ai或是原子，或是一个广义表。

• 广义表通常记作：LS=（a1,a2,…,an）
  其中:LS为表名，n为表的长度，每一个ai为表的元素。
  习惯上，一般用大写字母表示广义表，小写字母表示原子。

• 表头：若LS非空（n>=1）,则第一个元素ai就是表头。
  记作head(LS) = ai
  注：表头可以是原子，也可以是子表。

• 表尾：除表头之外的其他元素组成的表。
  记作：tail(LS) = (a2,…,an).
  注：表尾不是最后一个元素，而是一个子表。

树

树的定义：
树是n（n>=0）个空结点的有限集。
若n=0，则称为空树；
若n>0,则它满足两个条件：
（1）有且仅有一个特定的称为根的结点；
（2）其余结点可分为m（m>=0）个互不相交的有限集。其中每一个集合本身又是一棵树，并称为根的子树。

树的基本术语

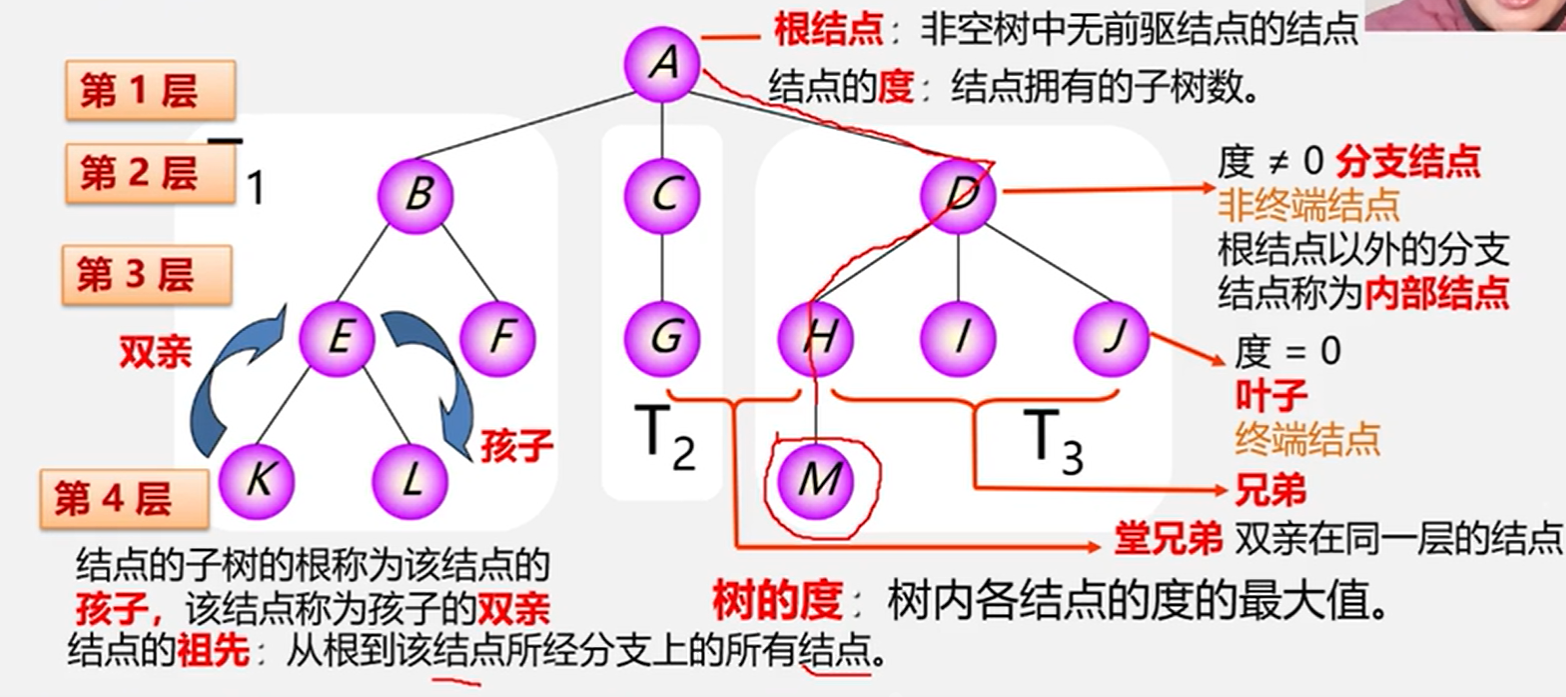
1. 根结点：非空树中无前驱的结点。
2. 结点的度：结点拥有的子树数。（度不等于0，分支结点非终端结点，根结点以外的分支结点称为内部结点；度等于0，叶子终端结点。）
3. 兄弟：双亲是同一个。
4. 堂兄弟：双亲在同一层的结点。
5. 树的度：树内各结点的度的最大值。
6. 树的深度：树中结点的最大层次。
7. 结点的子树的根称为该结点的孩子，该结点称为孩子的双亲结点的祖先。
8. 有序数：树中结点的各子树从左至右有次序。（最左边为第一个孩子）。
9. 无序树：树中结点的各子树无次序。
   10.森林：是m（m>=0）棵互不相交的树的集合。
   把根结点删除就变成了森林。

线性结构和树结构的比较

线性结构	树结构
第一个数据元素 无前驱	根结点（只有一个） 无双亲
最后一个数据元素 无后继	叶子结点（可以有多个） 无孩子
其他数据元素	其他结点----中间结点
一个前驱，一个后继	一个双亲，多个孩子
一对一	一对多

二叉树的定义

二叉树是n（n>=0个结点的有限集，它或者是空集（n=0），或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成）。
特点：1.每个结点最多有两孩子（二叉树中不存在度大于2的结点）。
2.子树有左右之分，其次序不能颠倒。
3.二叉树可以是空集合，根可以有空的左子树或空的右子树。
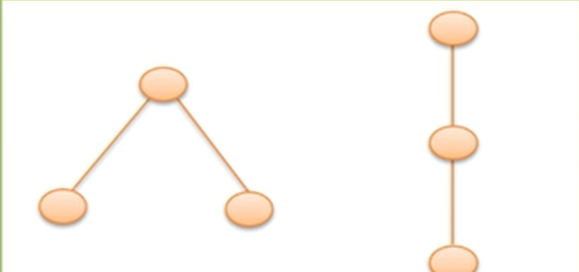
具有3个结点的二叉树可能有几种不同的形态？普通树呢？
二叉树的5种形态：

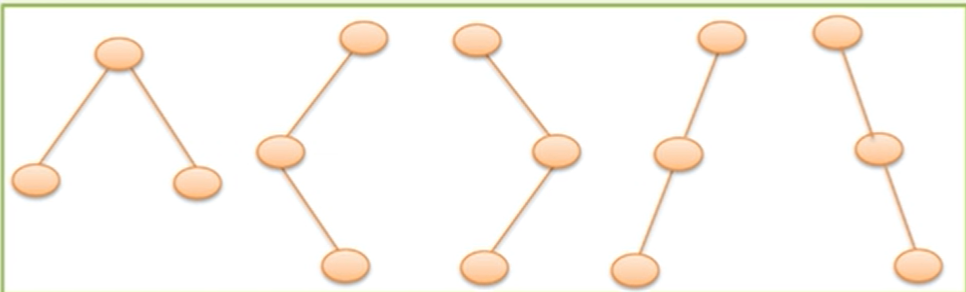
树的两种形态：

案例

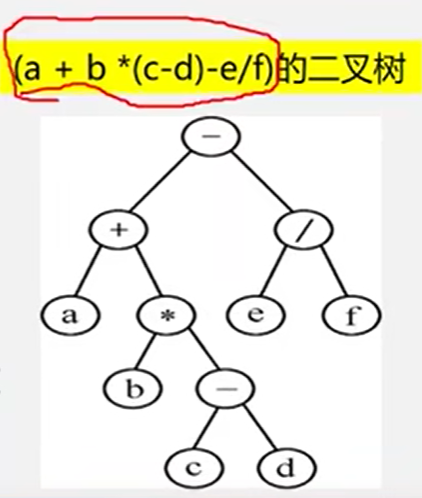
用树表示运算符

二叉树的性质和存储结构

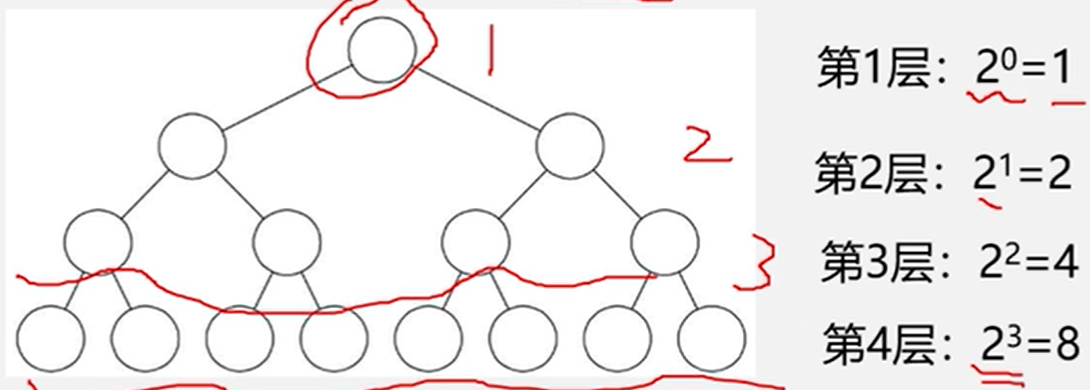
性质1：在二叉树的第i层上至多有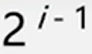个结点（i>=1）。

性质2：深度为k的二叉树至多有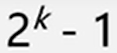个结点（k>=1）。
深度为k时至少有k个结点。
性质3：对任何一棵二叉树T，如果其叶子数为n0，度为2的结点数为n2，则n0=n2+1。

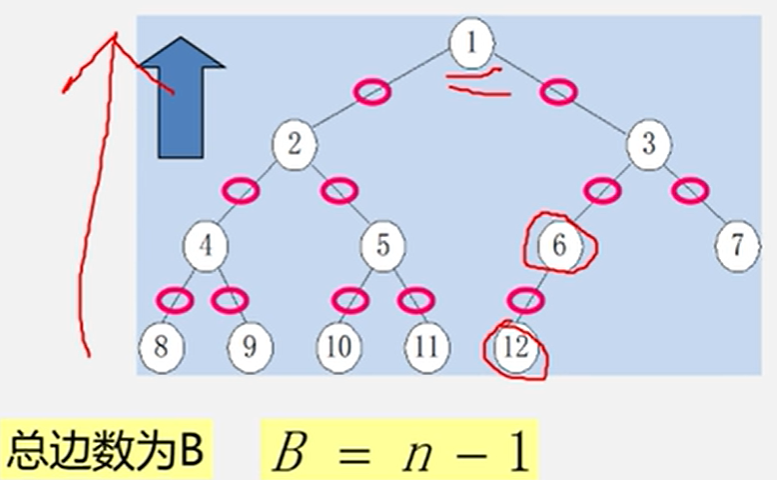因为根结点没有前驱，所以边数-1。

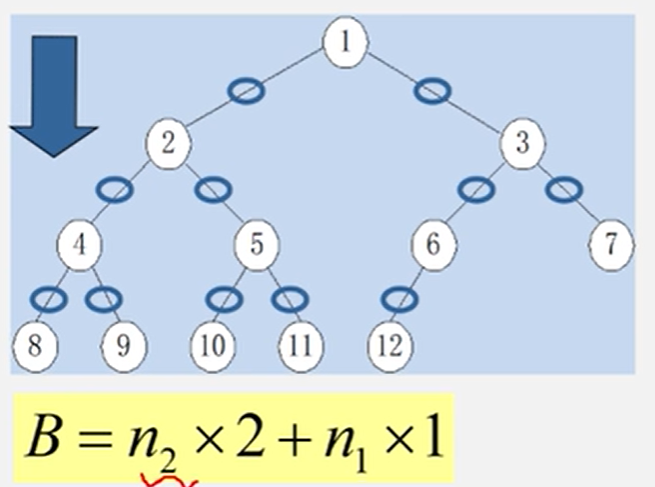
最后两边相等。

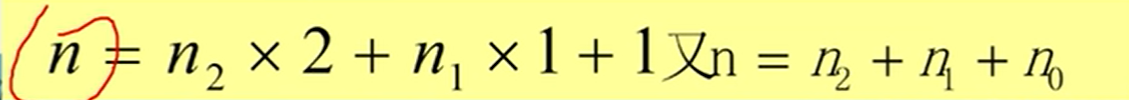
两种特殊形式下的二叉树

研究他们的原因：因为他们在顺序存储方式下可以复原。

满二叉树

一棵深度为k且有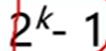个结点的二叉树称为慢二叉树。
特点：每一层上的结点数都是最大结点数（即每层都满），叶子结点全部都在底层。
对满二叉树结点位置进行编号：（1）自上而下，自左而右。（2）每一节点位置都有元素。

完全二叉树

深度为k的具有n个结点的二叉树，当且仅当每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树。
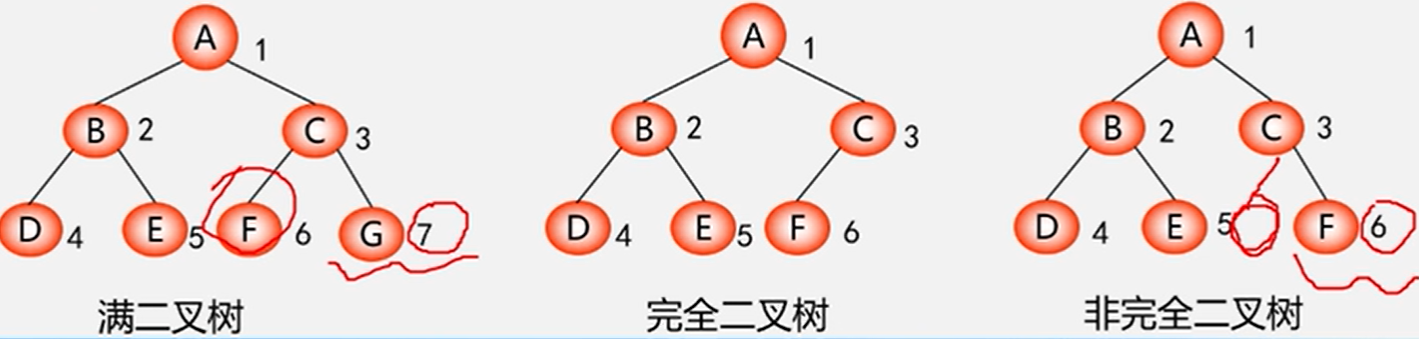注：在满二叉树中，从最后一个结点开始，连续去掉任意个结点，即一棵完全二叉树。
一定是连续去掉！！！

完全二叉树的性质

性质4：具有n个结点的称为完全二叉树的深度为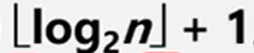注：称为x的底，表示不大于x的最大整数。
性质4表明了完全二叉树结点数n与完全二叉树深度k之间的关系。

性质5：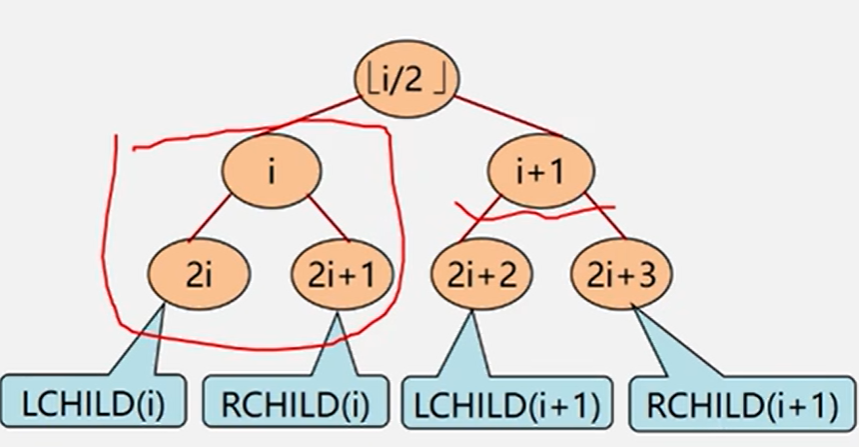

二叉树的存储结构

二叉树的存储结构分为顺序存储结构，链式存储结构（二叉链表，三叉链表）。

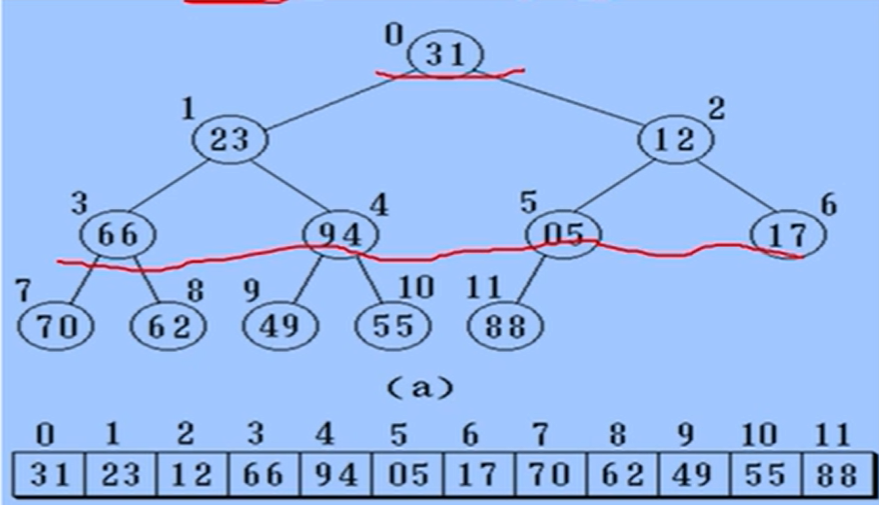
二叉树的顺序存储结构

实现：按满二叉树的结点层次编号，依次存放二叉树中的数据元素。

#define MAXTAIZE 100
#define TElemType int

//二叉树的顺序存储
typedef TElemType SqBiTree[MAXTAIZE];
SqBiTree bt;

例：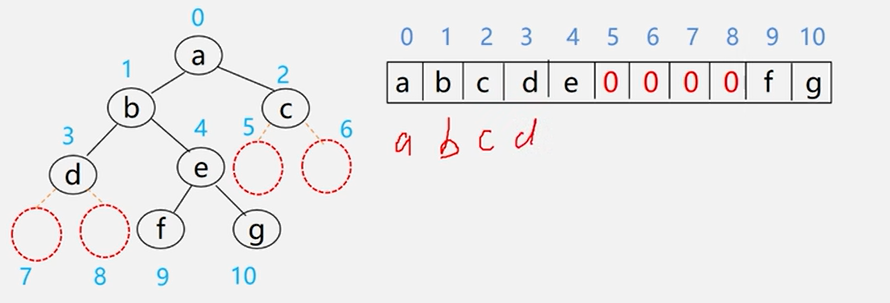

二叉树的链式存储结构

二叉树节点的特点：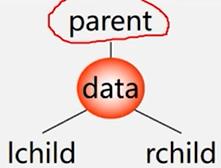
结点结构：

#define TElemType int

typedef struct BiNode {
	TElemType data;
	struct BiNode* lchild, * rchild;//左右孩子指针
}BiNode,*BiTree;

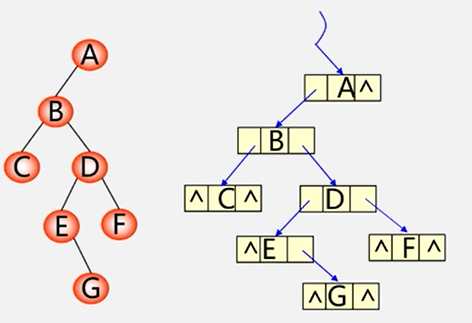
在n个结点的二叉树链表中，有n+1个空指针域。

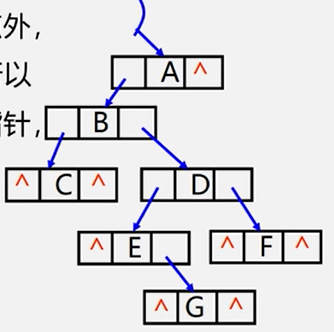
必有2n个链域，除根结点外，每一个结点有且仅有一个双亲，所以会有n-1个结点存放链域或指针域，指向非空子女结点。

三叉链表

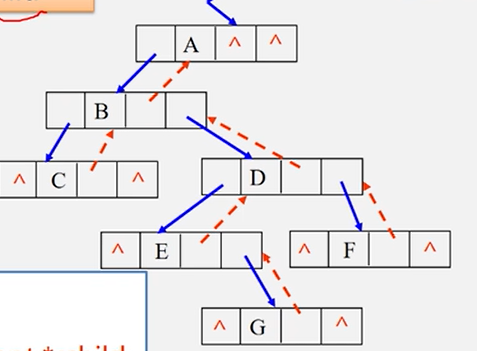
typedef struct TriTNode {
	TElemType data;
	struct BiNode* lchild, * rchild,*rchild;//左右孩子指针
}TriTNode, * TriTree;