一、滑模控制设计思路
参考资料:https://zhuanlan.zhihu.com/p/463230163(思路理解)
https://blog.csdn.net/xiaohejiaoyiya/article/details/90271529(干扰的处理)
- 滑模控制的思路有两个关键,一个是设计滑模面,另一个是李雅普诺夫反推滑模面控制律
1、设计滑模面
- 滑模面有很多种,线性、二次型等,这里介绍线性的,选择何种滑模面的关键是看被控对象的
- 滑模面数学形式如下:

当s=0时,根据微分方程的分离变量法,可知误差e指数级趋于0
2、李雅普诺夫反推滑模面s控制律
- 通过上面的论述可知,一旦s趋于0,则误差也会趋于0。至此,问题从设计控制律u使得误差e趋于0,变成了设计控制律u使得s趋于0。
- 如果增加控制律后,系统关于s的李雅普诺夫函数符合稳定性判定条件,则在有限时间内s一定会趋于0。进而,问题转变成了设计控制律使得关于s的李雅普诺夫函数符合收敛条件。
二、举例计算
1、控制对象动力学模型

2、控制目标
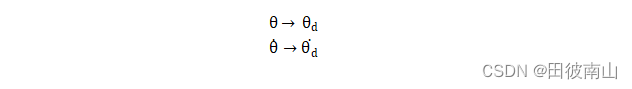
3、设计滑模面
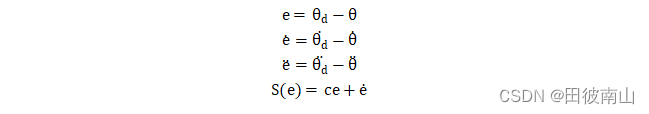
- 这里考虑轨迹跟踪问题,θd也是关于时间的函数
4、设计李雅普诺夫函数
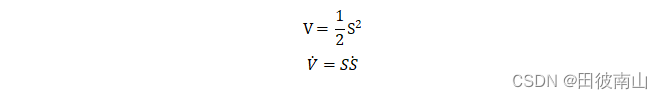
5、反推控制律
(1)分析李雅普诺夫函数V
- 根据李雅普诺夫的判定性质,只要V>0,
V
˙
\dot{V}
V˙<0,即可证明稳定。V明显大于0,所以重点是
V
˙
\dot{V}
V˙的分析。

根据上式可知,只要设计合适的控制量u,使得 V ˙ \dot{V} V˙小于0,即可达到目标。
(2)反推控制器u
- 之后就要去反推了,相较于靠直觉写控制器再用李雅普诺夫函数判定要明确了许多,但是仍然没那么好写。幸好已经有人总结了常见的设计方法,也就是
V
˙
\dot{V}
V˙的趋近律。常见的趋近律如下所示:
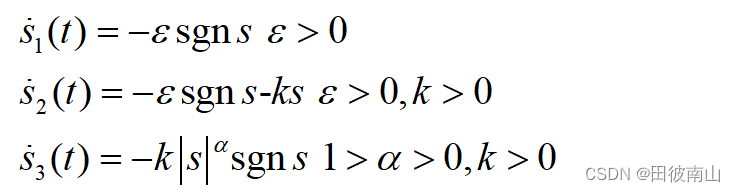
分别为等速、指数、幂次趋近律 - 以等速趋近律为例,分析李雅普诺夫条件

- 根据趋近律计算控制器
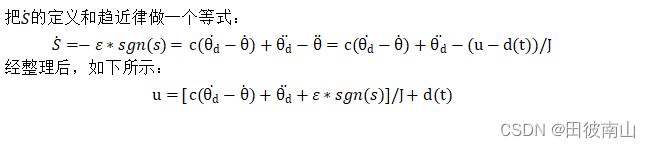
(3)处理干扰项d
-
离完成控制器的设计还有最后一项d要处理,在上面提到的控制律中存在干扰d,可是干扰本来就没法测量。看到过有人在分析这里时,直接给出一个干扰最大值,然后和趋近律合并在一起,这就比较难理解为什么了,合并后一定符合李雅普诺夫条件吗?当然,经过计算其实是符合的,否则人家也不会那么写,但是确实比较难理解。
-
可以先不管干扰d,直接用没有d的控制律做u,控制律如下所示:

-
在保持控制律的情况下,重新在 θ ¨ \ddot{θ} θ¨和u的关系中考虑d,再进行李雅普诺夫分析
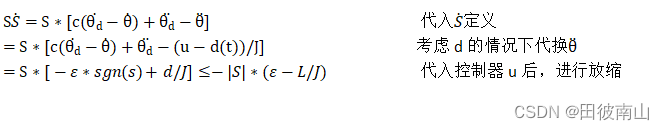
这里最后那个放缩不容易一眼看出来,代几个数进去应该是正确的,人家推到最后都是直接L,不知道为啥这里有个J,但是这是惯量常数,影响不大。 -
如果想 V ˙ \dot{V} V˙小于0,则ε要大于L/J。所以控制器中的ε是一个大于L/J的值,而下面截图中(图里ε对应η)这种将两个参数合并的写法,ε只要大于0即可,所以二者实质是一样的
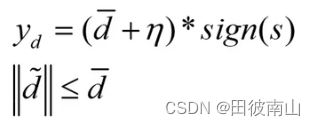
三、基于计算力矩法的滑模控制
参考:https://www.bilibili.com/video/BV13N4y1k7Cb/?spm_id_from=333.1007.top_right_bar_window_default_collection.content.click&vd_source=a686d8f8b0e9b94066f2d4ba714466e7
- 可以想一想上面说的干扰d到底对应着什么,可以是外力扰动,比如风阻、摩擦;甚至可以是动力学模型参数中的误差。这里之前有一个误解,以为模型中的耦合项c也可以认为是干扰,实际是不行的,因为其变化比较大,这里使用计算力矩法规避了这一问题,并使用鲁棒项抑制了误差。

截图中,最后说系统变成了一个带干扰的线性系统,实际就是将所有参数误差全看成了干扰。比较特别的点在于定义了一个间接控制量v,建立v的控制器后,力矩T可以通过v计算。v控制器的建立过程就和普通滑模控制器的建立过程没有区别。