文章目录
- 01 概述与预备知识
- 1.1 SLAM 是什么
- 1.1.1 基本概念
- 1.1.2 视觉 SLAM 框架
- 1.1.3 SLAM 问题的数学表述
- 1.2 实践:编程基基础
- 1.3 课后习题
01 概述与预备知识
1.1 SLAM 是什么
1.1.1 基本概念
(1)SLAM 是 Simultaneous Localization and Mapping 的缩写,即同时定位与地图构建。它是指搭载特定传感器的主体,在没有环境先验信息的情况下,于运动过程中建立环境的模型。
(2)两大基本问题:
-
定位:我在什么地方?
-
建图:周围环境是什么样的?
(3)准确的定位需要精确的地图,精确的地图来自准确的定位。
(4)传感器
-
内质的(放置在机器人身上,用于感受机器人本体信息):IMU(惯性测量单元)、激光、相机
-
外质的(安装于环境中,监测机器人的运动状态):二维码、GPS导轨
(5)相机
以一定速率采集图像,形成视频。相较于激光传感器更便宜,信息更丰富。
相机以二维投影形式记录三维世界的信息,丢掉了距离信息。
分类:
-
单目相机:最常见的普通相机
-
双目相机(立体相机):类似于人眼,通过视差计算出距离信息
-
深度相机(RGB-D):发射端、接收端,获得RGB图和深度图
-
其他:全景相机、事件相机
1.1.2 视觉 SLAM 框架
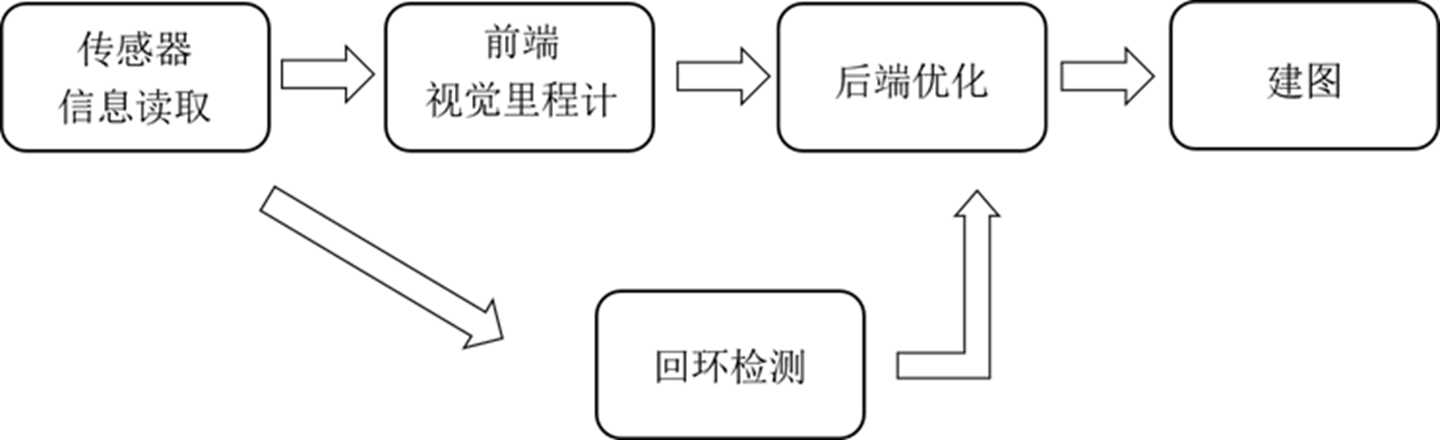
-
前端:Visual Odometry(VO),视觉里程计的任务是估算邻近时刻的相机运动。主要方法:特征点法、直接法
-
后端:Optimization,从带有噪声的数据中估计最优轨迹与地图。常用方法:最大后验估计、滤波器、图优化。
-
回环检测:Loop Closing,主要解决位置估计随时间漂移的问题。判断机器人是否到达过先前的位置,如果检测到回环,将信息提供给后端进行处理。
-
建图:Mapping,根据估计的轨迹,建立地图。主要分为度量地图和拓扑地图两类。度量地图又分为稀疏地图和稠密地图,稀疏地图比较抽象,仅包含一部分有意义的信息——地标。进行导航时,就需要稠密地图(避免碰撞某些障碍物)。
1.1.3 SLAM 问题的数学表述
(1)数学表述
两个方程:运动方程和观测方程
{ x k = f ( x k − 1 , u k , w k ) z k , j = h ( y j , x k , v k , j ) (1-1) \left\{ \begin{matrix} \boldsymbol{x_k}=f(\boldsymbol{x_{k-1}},\boldsymbol{u_k}, \boldsymbol{w_k}) \\ \boldsymbol{z_{k,j}}=h(\boldsymbol{y_j},\boldsymbol{x_k},\boldsymbol{v_{k,j}}) \end{matrix} \right. \tag{1-1} {xk=f(xk−1,uk,wk)zk,j=h(yj,xk,vk,j)(1-1)
这里, x k \boldsymbol{x_k} xk 为 k k k 时刻的位置, u k \boldsymbol{u_k} uk 是运动传感器的读数或输入,比如相对上一位置前进1 m 或左转 10°; w k \boldsymbol{w_k} wk 为噪声。 z k , j \boldsymbol{z_{k,j}} zk,j 为机器人在 x k \boldsymbol{x_k} xk 位置时对路标 y j \boldsymbol{y_j} yj 的观测数据, v k , j \boldsymbol{v_{k,j}} vk,j 为此次观测的噪声。
对于简单的平面运动,机器人的位姿由横纵坐标和转角组成 x k = [ x 1 , x 2 , θ ] T \boldsymbol{x_k}=[x_1, x_2, \theta ]^T xk=[x1,x2,θ]T,变化量 u k = [ Δ x 1 , Δ x 2 , Δ θ ] T \boldsymbol{u_k}=[\Delta x_1, \Delta x_2, \Delta\theta ]^T uk=[Δx1,Δx2,Δθ]T,则运动方程可简化为
[ x 1 x 2 θ ] k = [ x 1 x 2 θ ] k − 1 + [ Δ x 1 Δ x 2 Δ θ ] k + w k (1-2) \left[\begin{matrix} { x }_{ 1 } \\ { x }_{ 2 } \\ \theta \end{matrix}\right]_k = \left[\begin{matrix} { x }_{ 1 } \\ { x }_{ 2 } \\ \theta \end{matrix}\right]_{k-1} + \left[\begin{matrix} \Delta{ x }_{ 1 } \\\Delta{ x }_{ 2 } \\\Delta\theta \end{matrix}\right]_{k} + \boldsymbol{w_k} \tag{1-2} x1x2θ k= x1x2θ k−1+ Δx1Δx2Δθ k+wk(1-2)
对于观测方程,以激光传感器为例,可以测量出此位置和路标之间的距离 r r r 和夹角 ϕ \phi ϕ,路标点位置记为 y j = [ y 1 , y 2 ] T j \boldsymbol{y_j}=[y_1, y_2]^{T_j } yj=[y1,y2]Tj,位姿为 x k = [ x 1 , x 2 ] T j \boldsymbol{x_k}=[x_1, x_2]^{T_j } xk=[x1,x2]Tj ,观测数据为 z k , j = [ r k , j , ϕ k , j ] T \boldsymbol{z_{k,j}}=[r_{k,j}, \phi_{k,j}]^{T} zk,j=[rk,j,ϕk,j]T,在笛卡尔坐标系中,可以写为
[ r k , j ϕ k , j ] = [ ( y 1 , j − x 1 , k ) 2 + ( y 2 , j − x 2 , k ) 2 a r c t a n ( y 2 , j − x 2 , k ) ( y 1 , j − x 1 , k ) ] + v (1-3) \left[\begin{matrix} r_{k,j} \\\phi_{k,j} \end{matrix}\right] = \left[\begin{matrix} \sqrt{{(y_{1,j}}-x_{1,k})^2+{(y_{2,j}}-x_{2,k})^2} \\ arctan{ (y_{2,j}-x_{2,k}) \over (y_{1,j}-x_{1,k})} \end{matrix}\right] + \boldsymbol{v} \tag{1-3} [rk,jϕk,j]=[(y1,j−x1,k)2+(y2,j−x2,k)2arctan(y1,j−x1,k)(y2,j−x2,k)]+v(1-3)
当然,对于三维空间中的运动或其他形式传感器,上式有不同的参数化形式。
(2)SLAM 是一个状态估计问题
按运动和观测方程是否为线性,噪声是否符合高斯分布,分为线性/非线性和高斯/非高斯系统。
-
线性高斯系统: 卡尔曼滤波
-
非线性非高斯系统: 扩展卡尔曼滤波、非线性优化
1.2 实践:编程基基础
- Ubuntu 系统
- C++
- 编辑器:Clion、VS Code
- 工具:cmake
- 库:Eigen、G2O、Ceres、OpenCV等





![[动态规划] (五) 路径问题: LeetCode 62.不同路径](https://img-blog.csdnimg.cn/img_convert/4465b4b8a6bfc9890497cf1fdec97321.png)





![旋转图像[中等]](https://img-blog.csdnimg.cn/040f90bbd07b4545bf54158d772588f7.png)