优质博文：IT-BLOG-CN

一、题目

给定一个n × n的二维矩阵matrix表示一个图像。请你将图像顺时针旋转90度。你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1：

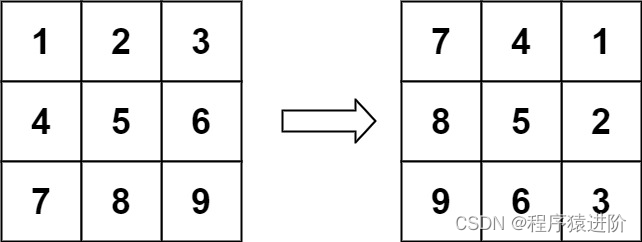
输入： matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出： [[7,4,1],[8,5,2],[9,6,3]]

示例 2：

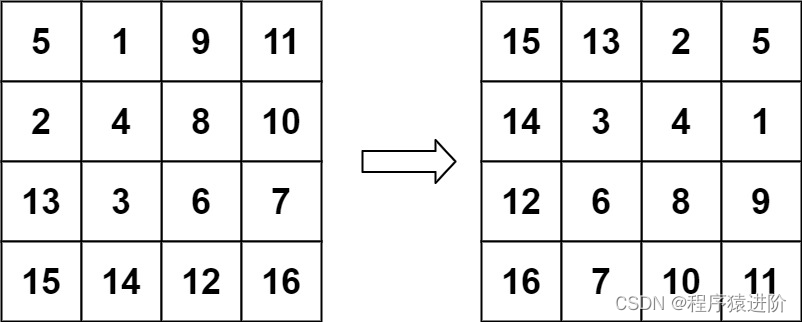
输入： matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出： [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

二、代码

【1】我们先不进行原地旋转，而是使用辅助数组进行，我们通过案例寻找规律：

[5  1  9  11]
[2  4  8  10]       
[13 3  6  7 ]         
[15 14 12 16]

我们将图像旋转90度之后，我们看下第一行，旋转后他出现在倒数第一列的位置：可以发现第一行的x元素落到了倒数第一列的第x个元素。

[5  1  9  11]                 [o  o  o  5] 
[o  o  o  o ]  ----> 旋转后   [o  o  o  1] 
[o  o  o  o ]                 [o  o  o  9] 
[o  o  o  o ]                 [o  o  o 11] 

对于矩阵中的第二行，我们旋转后看下：对于矩阵中的第三行和第四行同理。这样我们可以得到规律：**对于矩阵中第i行的第j个元素，在旋转后，它出现在倒数第i列的第j个位置。**我们将其翻译成代码。由于矩阵中的行列从0开始计数，因此对于矩阵中的元素matrix[row][col]，在旋转后，它的新位置为matrixnew[col][n−1−row]。

[o  o  o  o ]                 [o  o  2  o] 
[2  4  5  10]  ----> 旋转后   [o  o  3  o] 
[o  o  o  o ]                 [o  o  4  o] 
[o  o  o  o ]                 [o  o  10 o] 

我们使用一个与matrix大小相同的辅助数组matrixnew​，临时存储旋转后的结果。我们遍历matrix中的每一个元素，根据上述规则将该元素存放到matrixnew 中对应的位置。在遍历完成之后，再将matrixnew中的结果复制到原数组中即可。

class Solution {
    public void rotate(int[][] matrix) {
        // 先创建相同的二位数据进行优化
        int n = matrix.length;
        int[][] matrixNew = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrixNew[j][n-1-i] = matrix[i][j];
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                matrix[i][j] = matrixNew[i][j];
            }
        }
    }
}

时间复杂度： O(N2)其中N是matrix的边长。
空间复杂度： O(N2)我们需要使用一个和matrix大小相同的辅助数组。

【2】去除额外空间，使用原地旋转：我们尝试在不使用额外内存空间的情况下进行矩阵的旋转，那么如何在方法一的基础上完成原地旋转呢？

我们观察方法一中的关键等式：matrixnew​[col][n−row−1]=matrix[row][col] 它阻止了我们进行原地旋转，这是因为如果我们直接将matrix[row][col]放到原矩阵中的目标位置matrix[col][n−row−1]，原矩阵中的matrix[col][n−row−1]就被覆盖了！这并不是我们想要的结果。因此我们可以考虑用一个临时变量temp暂存matrix[col][n−row−1]的值，这样虽然matrix[col][n−row−1]被覆盖了，我们还是可以通过temp获取它原来的值：

temp                 = matrix[col][n−row−1]
matrix[col][n−row−1] = matrix[row][col]​

那么matrix[col][n−row−1]经过旋转操作之后会到哪个位置呢？我们还是使用方法一中的关键等式，不过这次，我们需要将

row ​= col
col ​= n−row−1​

带入关键等式，就可以得到：

matrix[n−row−1][n−col−1] = matrix[col][n−row−1]

同样地，直接赋值会覆盖掉matrix[n−row−1][n−col−1]原来的值，因此我们还是需要使用一个临时变量进行存储，不过这次，我们可以直接使用之前的临时变量temp：

temp                     ​= matrix[n−row−1][n−col−1]
matrix[n−row−1][n−col−1] = matrix[col][n−row−1]
matrix[col][n−row−1]     ​= matrix[row][col]

我们再重复一次之前的操作matrix[n−row−1][n−col−1]经过旋转操作之后会到哪个位置呢？

row ​= n−row−1
col ​= n−col−1​

带入关键等式，就可以得到：matrix[n−col−1][row]=matrix[n−row−1][n−col−1]写进去：

temp                      ​= matrix[n−col−1][row]
matrix[n−col−1][row]      = matrix[n−row−1][n−col−1]
matrix[n−row−1][n−col−1]  = matrix[col][n−row−1]
matrix[col][n−row−1]      = matrix[row][col]

再来一次matrix[n−col−1][row]经过旋转操作之后回到哪个位置呢？

row ​= n−col−1
col ​= row

带入关键等式，就可以得到：matrix[row][col]=matrix[n−col−1][row]我们回到了最初的起点matrix[row][col]，也就是说：

​matrix[row][col]
matrix[col][n−row−1]
matrix[n−row−1][n−col−1]
matrix[n−col−1][row]

这四项处于一个循环中，并且每一项旋转后的位置就是下一项所在的位置！因此我们可以使用一个临时变量temp完成这四项的原地交换：

temp                     ​= matrix[row][col]
matrix[row][col]         ​​= matrix[n−col−1][row]
matrix[n−col−1][row]     = matrix[n−row−1][n−col−1]
matrix[n−row−1][n−col−1] = matrix[col][n−row−1]
matrix[col][n−row−1]     = temp​

当我们知道了如何原地旋转矩阵之后，还有一个重要的问题在于：我们应该枚举哪些位置(row,col)进行上述的原地交换操作呢？由于每一次原地交换四个位置，因此：
【1】当n为偶数时，我们需要枚举n^2/4=(n/2)×(n/2)个位置，可以将该图形分为四块，以4×4的矩阵为例：保证了不重复、不遗漏；

【2】当n为奇数时，由于中心的位置经过旋转后位置不变，我们需要枚举(n^2−1)/4=((n−1)/2)×((n+1)/2)个位置，需要换一种划分的方式，以5×5的矩阵为例：同样保证了不重复、不遗漏，矩阵正中央的点无需旋转。

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
}

时间复杂度： O(N^2)其中N是matrix的边长。我们需要枚举的子矩阵大小为O(⌊n/2⌋×⌊(n+1)/2⌋)=O(N^2)。
空间复杂度： O(1)为原地旋转。

【3】用翻转代替旋转： 我们还可以另辟蹊径，用翻转操作代替旋转操作。我们还是以题目中的示例二

[5  1  9  11]
[2  4  8  10]       
[13 3  6  7 ]         
[15 14 12 16]

作为例子，先将其通过水平轴翻转得到：

[5  1  9  11]                [15 14 12 16]
[2  4  8  10]    -->反转后    [13 3  6  7] 
[13 3  6  7 ]                [2  4  8  10] 
[15 14 12 16]                [5  1  9  11] 

再根据主对角线翻转得到：

[5  1  9  11]                [15 13 2  5]
[2  4  8  10]    -->反转后    [14 3  4  1] 
[13 3  6  7 ]                [12 6  8  9] 
[15 14 12 16]                [16 7 10  11] 

就得到了答案。这是为什么呢？对于水平轴翻转而言，我们只需要枚举矩阵上半部分的元素，和下半部分的元素进行交换，即matrix[row][col]水平轴翻转​matrix[n−row−1][col]对于主对角线翻转而言，我们只需要枚举对角线左侧的元素，和右侧的元素进行交换，即matrix[row][col]主对角线翻转​matrix[col][row]将它们联立即可得到：

matrix[row][col]  ​水平轴翻转     ​matrix[n−row−1][col]
                  主对角线翻转   ​matrix[col][n−row−1]​

和方法一、方法二中的关键等式：matrixnew​[col][n−row−1]=matrix[row][col]是一致的。

class Solution {
    public void rotate(int[][] matrix) {
        // 思想：翻转代替旋转，先上下翻转在对角线翻转
        int n = matrix.length;
        // 上下翻转
        for (int i = 0; i < n/2; i++) {
            for (int j = 0; j < n; j++) {
                int temp = matrix[n-1-i][j];
                matrix[n-1-i][j] = matrix[i][j];
                matrix[i][j] = temp;
            }
        }

        // 对角线翻转
        for (int i = 0; i < n; i++) {
            for (int j = 0; j <= i; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }
}

时间复杂度：O(N^2)，其中N是matrix的边长。对于每一次翻转操作，我们都需要枚举矩阵中一半的元素。
空间复杂度： O(1)。为原地翻转得到的原地旋转。