汉诺塔

汉诺塔（Tower of Hanoi）（河内塔）：把圆盘从下面开始按大小顺序重新摆放到另一根柱子上，并且小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

---

  汉诺塔规则

•  disk表示圆盘数
• 一次只能移动一个圆盘
• 小圆盘只能在大圆盘的上方
• A 、B 、C分别表示圆柱
• A为起始圆柱、B为中转圆柱、C为终止圆柱

---

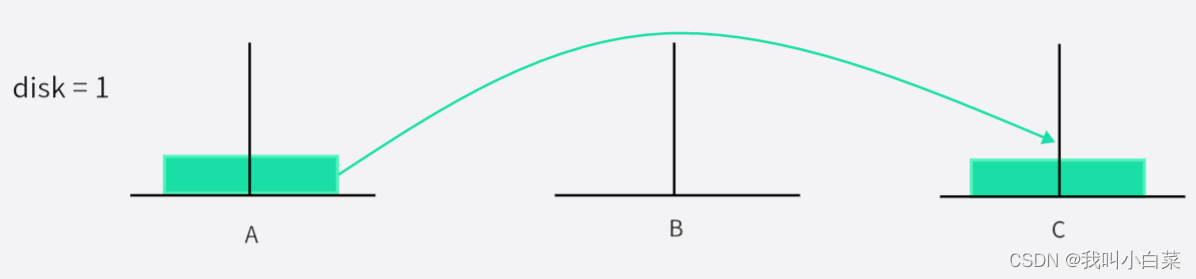
disk = 1 时：

移动次数为：2^1 - 1

只需要将绿色圆盘从 A->C 直接移过去；

A->C

---

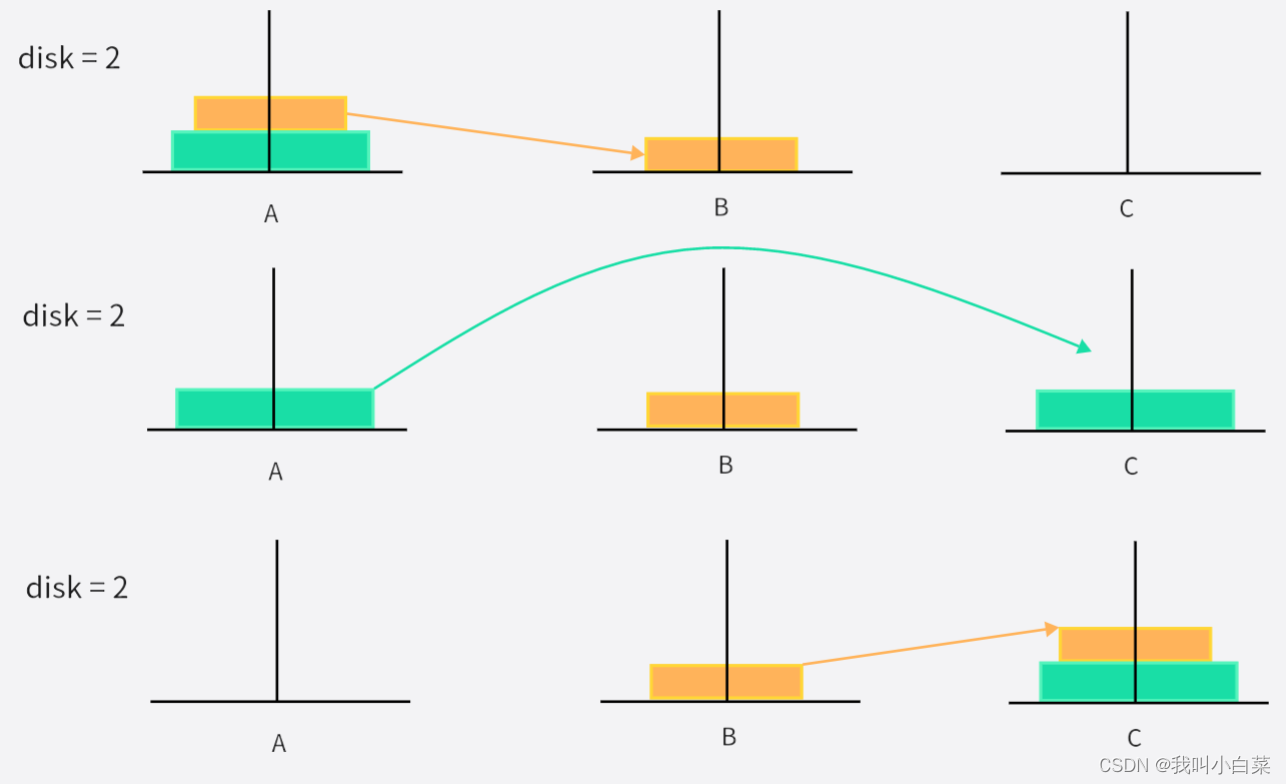
disk = 2 时：

移动次数为：2^2 - 1，一次只能移动一个圆盘

1. 黄色圆盘从 A->B
2. 绿色圆盘从 A->C
3. 黄色圆盘从 B->C

A->B  A->C  B->C

---

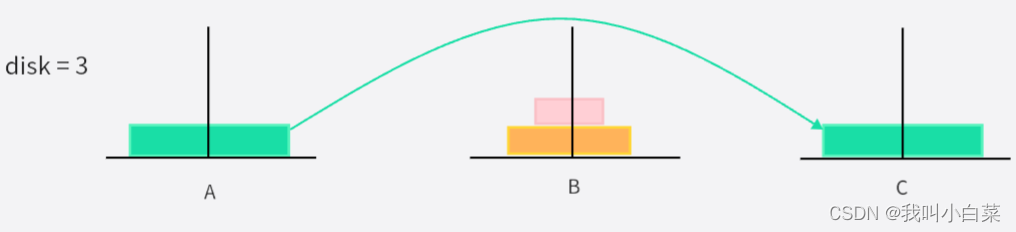
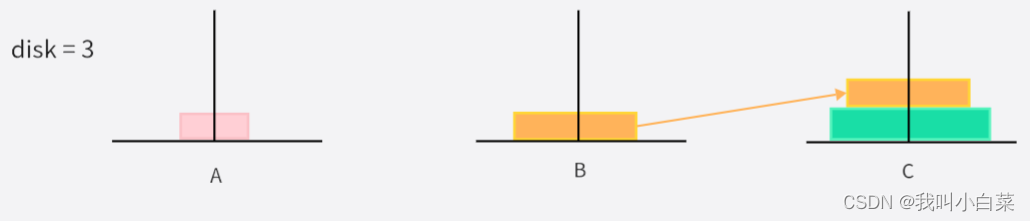
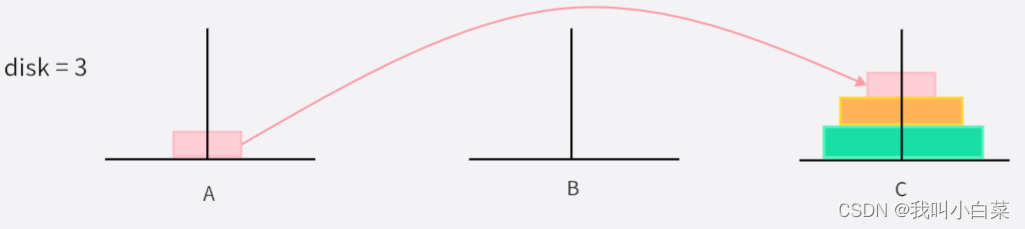
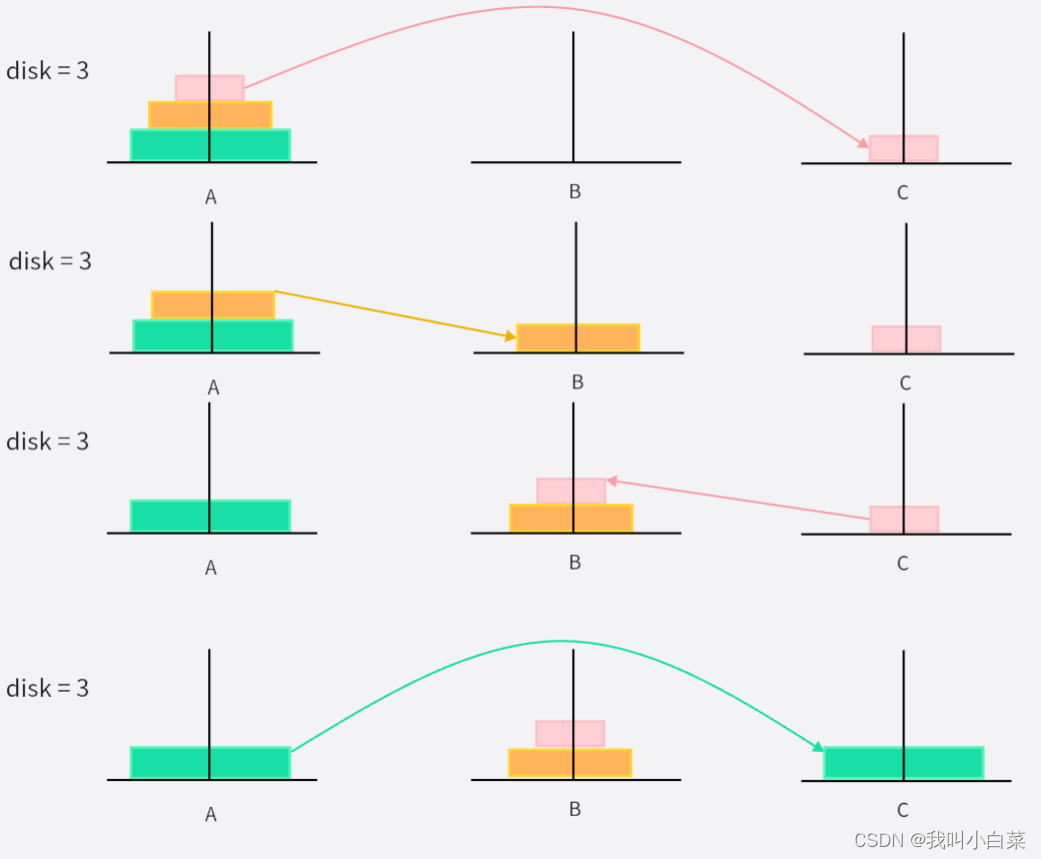
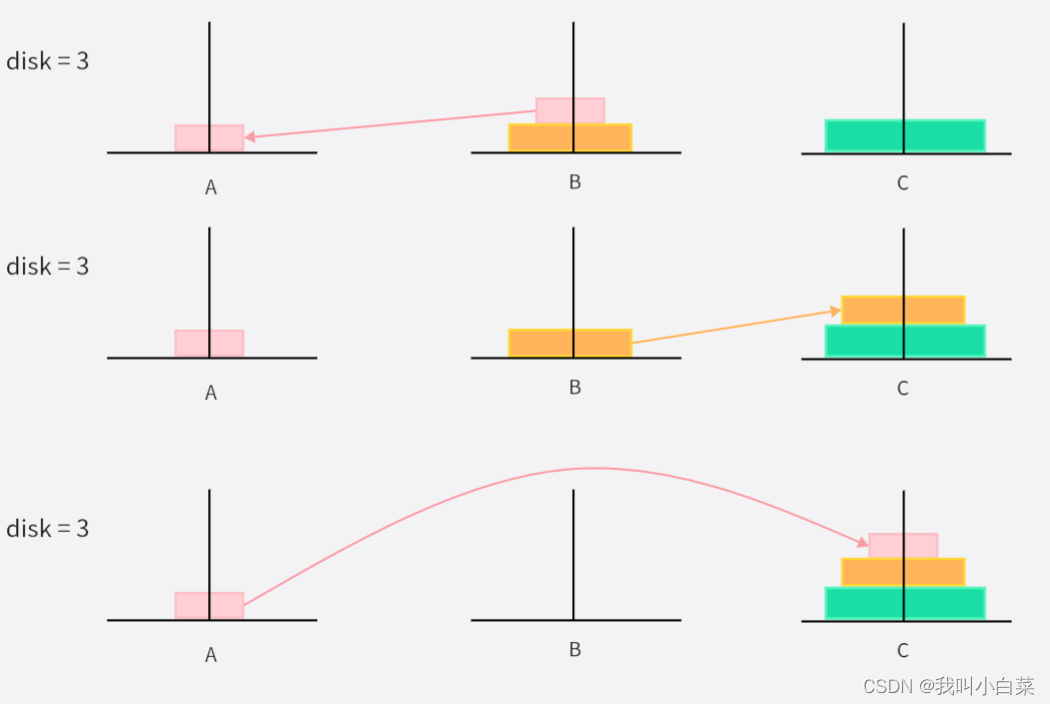
disk = 3 时：

移动次数为：2^3 - 1，一次只能移动一个圆盘

1. 粉色圆盘从 A->C
2. 黄色圆盘从 A->B
3. 粉色圆盘从 C->B
4. 绿色圆盘从 A->C
5. 粉色圆盘从 B->A
6. 黄色圆盘从 B->C
7. 粉色圆盘从 A->C

A->C  A->B  C->B  A->C  B->A  B->C  A->C

---

递归分析

1. 先看desk = 3 个圆盘时，我们是先将圆柱A上面的2个圆盘（3 - 1），借助圆柱C最终移动到圆柱B上；
2. 此时圆柱A上就只剩1个圆盘，就可以直接将圆盘从圆柱A移动到圆柱C；

---

1. desk = 2个圆盘，先将圆柱B上面的那1个圆盘（2 - 1），最终直接从圆柱B移动到圆柱A上；
2. 此时圆柱B上就只剩1个圆盘，就可以直接从圆柱B移动到圆柱C上；

---

1. 只剩最后1个圆盘了，则是直接从圆柱A上移动到圆柱C上；

---

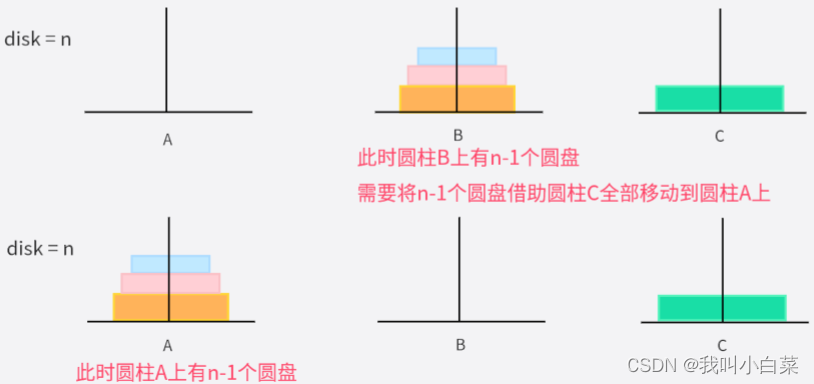
 disk = n 时：

移动次数为：2^n - 1，一次只能移动一个圆盘

错误递归分析

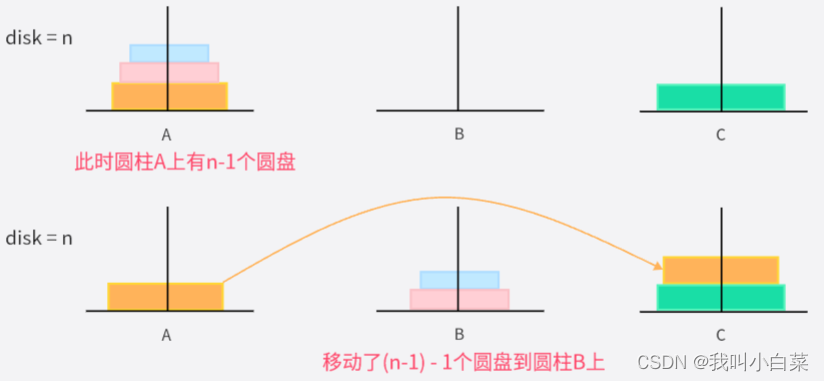
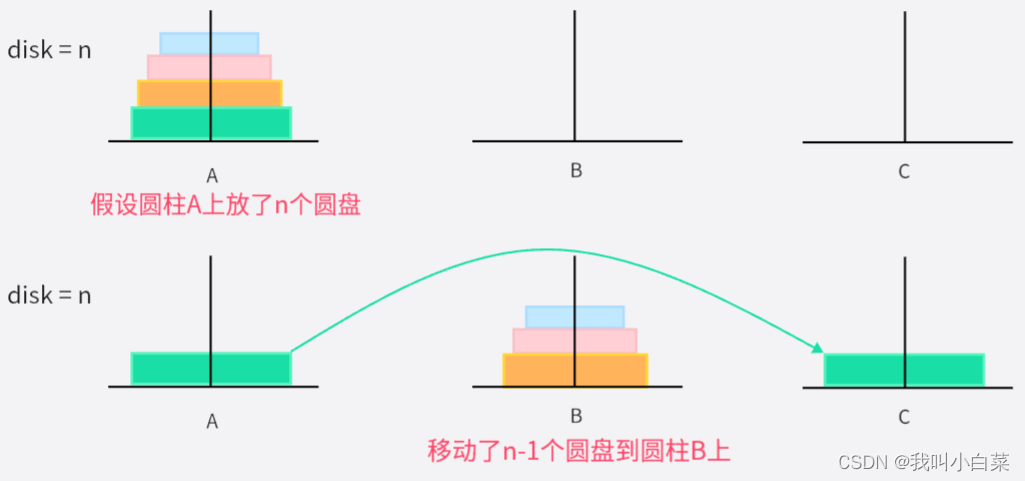
1.  当desk = n个圆盘时，需要将圆柱A上面的n-1个圆盘，借助圆柱C最终移动到圆柱B上；
2. 此时圆柱A上就只剩1个圆盘，则直接从圆柱A移动到圆柱C；

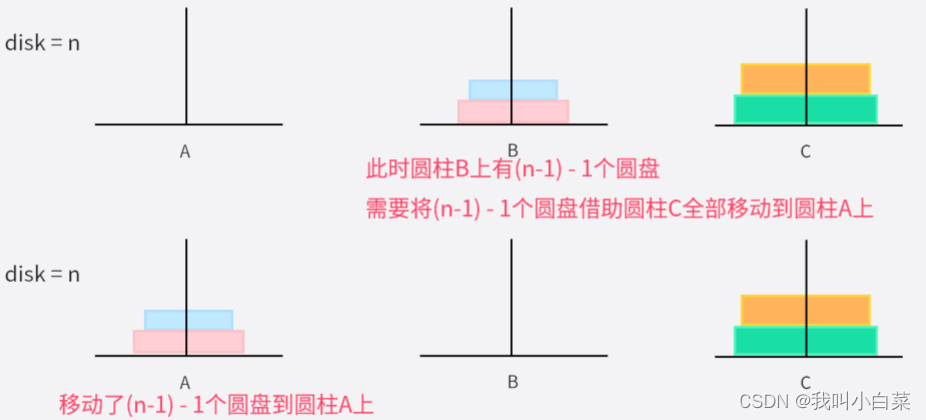
1.  desk = n 时，先将圆柱B上面的n-1个圆盘，借助圆柱C最终移到圆柱A上；
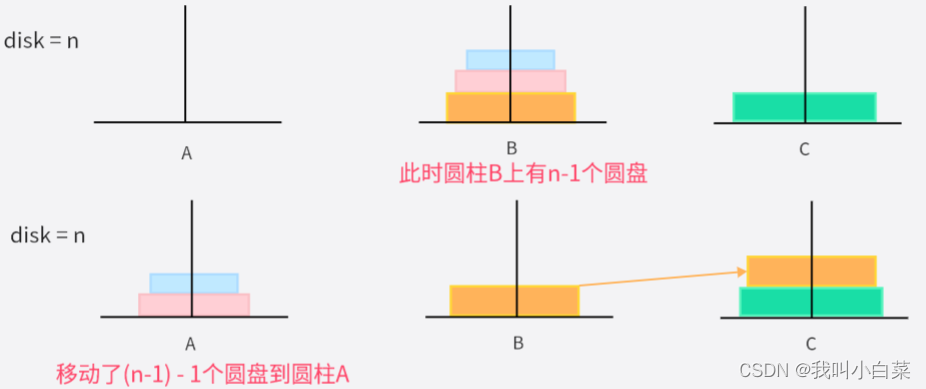
2. 此时圆柱A上有n-1个圆盘，递归以上步骤；

---

1. 当 desk = n-1时，需要将圆柱A上面的(n-1) - 1个圆盘，借助圆柱C移到圆柱B上（这里已经在开始和desk = n 的情况一样）；
2. 此时圆柱A上就只剩1个圆盘，则直接从圆柱A移动到圆柱C；

1. desk = n-1时，先将圆柱B上面的(n-1) - 1个圆盘，借助圆柱C最终移到圆柱A上；
2. 此时圆柱A上有(n-1) - 1个圆盘，递归以上步骤；

---

错误代码分析

public class TowerOfHanoi {
    public static void hanoi(int n, char posA, char posB, char posC) {
        // hanoi(圆盘个数，参数1，参数2，参数3)
        // 参数1表示起始位置、参数2表示中转位置、参数3表示终止位置
        if(n == 1) {
            move(posA, posC);
            return; // 递归一定要return
        }
        // 这一步就是将 圆柱A 上的 n-1个 圆盘
        // 借助圆柱C 移动到 圆柱B上
        hanoi(n-1, posA, posC, posB);

        // 将圆柱A上剩下的一个移到圆柱C上
        move(posA, posC);

        // 将 圆柱B 上的所有圆盘 借助圆柱C 移到圆柱A上
        hanoi(n-1, posB, posC, posA); // 这里是错的
    }
    public static void move(char pos1, char pos2) {
        System.out.println(pos1 + "->" + pos2);
    }
    public static void main(String[] args) {
        hanoi(3, 'A', 'B', 'C');
    }
}

---

 正确递归分析

1.  当desk = n个圆盘时，需要将圆柱A上面的n-1个圆盘，借助圆柱C最终移动到圆柱B上；
2. 此时圆柱A上就只剩1个圆盘，则直接从圆柱A移动到圆柱C；
3. 将圆柱B上的n-1个圆盘，借助圆柱A最终移动到圆柱C上；
4. 此时圆柱B上就只剩一个圆盘，则直接从圆柱B移动到圆柱C；

 

---

正确代码分析

public class TowerOfHanoi {
    public static void hanoi(int n, char posA, char posB, char posC) {
        // hanoi(圆盘个数，参数1，参数2，参数3)
        // 参数1表示起始位置、参数2表示中转位置、参数3表示终止位置
        if(n == 1) {
            move(posA, posC);
            return; // 递归一定要return
        }
        // 这一步就是将 圆柱A 上的 n-1个 圆盘
        // 借助圆柱C 移动到 圆柱B上
        hanoi(n-1, posA, posC, posB);

        // 将圆柱A上剩下的一个移到圆柱C上
        move(posA, posC);
        
        
        hanoi(n-1, posB, posA, posC);
    }
    public static void move(char pos1, char pos2) {
        System.out.println(pos1 + "->" + pos2);
    }
    public static void main(String[] args) {
        hanoi(3, 'A', 'B', 'C');
    }
}