• 签到送分题
• 模拟：让程序完整地按照题目叙述的方式最终得到答案。

模拟

[NOIP2003 普及组] 乒乓球

题目背景
国际乒联现在主席沙拉拉自从上任以来就立志于推行一系列改革，以推动乒乓球运动在全球的普及。其中 $11$ 分制改革引起了很大的争议，有一部分球员因为无法适应新规则只能选择退役。华华就是其中一位，他退役之后走上了乒乓球研究工作，意图弄明白 $11$ 分制和 $21$ 分制对选手的不同影响。在开展他的研究之前，他首先需要对他多年比赛的统计数据进行一些分析，所以需要你的帮忙。

题目描述

华华通过以下方式进行分析，首先将比赛每个球的胜负列成一张表，然后分别计算在 $11$ 分制和 $21$ 分制下，双方的比赛结果（截至记录末尾）。

比如现在有这么一份记录，（其中 $\text{W}$ 表示华华获得一分，$\text{L}$ 表示华华对手获得一分）：

$\text{WWWWWWWWWWWWWWWWWWWWWWLW}$

在 $11$ 分制下，此时比赛的结果是华华第一局 $11$ 比 $0$ 获胜，第二局 $11$ 比 $0$ 获胜，正在进行第三局，当前比分 $1$ 比 $1$。而在 $21$ 分制下，此时比赛结果是华华第一局 $21$ 比 $0$ 获胜，正在进行第二局，比分 $2$ 比 $1$。如果一局比赛刚开始，则此时比分为 $0$ 比 $0$。直到分差大于或者等于 $2$，才一局结束。

你的程序就是要对于一系列比赛信息的输入（$\text{WL}$ 形式），输出正确的结果。

输入格式

每个输入文件包含若干行字符串，字符串有大写的 $\text{W}$ 、 $\text{L}$ 和 $\text{E}$ 组成。其中 $\text{E}$ 表示比赛信息结束，程序应该忽略 $\text{E}$ 之后的所有内容。

**输出格式
**
输出由两部分组成，每部分有若干行，每一行对应一局比赛的比分（按比赛信息输入顺序）。其中第一部分是 $11$ 分制下的结果，第二部分是 $21$ 分制下的结果，两部分之间由一个空行分隔。

样例 #1

样例输入 #1

WWWWWWWWWWWWWWWWWWWW
WWLWE

样例输出 #1

11:0
11:0
1:1

21:0
2:1

提示

每行至多 $25$ 个字母，最多有 $2500$ 行。

（注：事实上有一个测试点有 $2501$ 行数据。）

【题目来源】

NOIP 2003 普及组第一题

#include<cmath>
#include<iostream>
using namespace std;

int f[2]={11,21};
int a[25*2500+10],n=0;

int main( ){
    char tmp;
    while(1){
        cin>>tmp;
        if(tmp=='E')break;
        if(tmp=='W')a[n++]=1;
        if(tmp=='L')a[n++]=0;
    }
    for(int i=0;i<2;i++){
        int w=0,l=0;
        for(int j=0;j<n;j++){
            w+=a[j];
            l+=(1-a[j]);

            if(max(w,l)>=f[i]&&abs(l-w)>=2){
               cout<<w<<":"<<l<<endl;
                w = l = 0;
            }
        }
        
        cout<<w<<":"<<l<<endl<<endl;
    }
    
    return 0;
}

[NOIP2015 普及组] 扫雷游戏

题目背景

NOIP2015 普及组 T2

题目描述

扫雷游戏是一款十分经典的单机小游戏。在 $n$ 行 $m$ 列的雷区中有一些格子含有地雷（称之为地雷格），其他格子不含地雷（称之为非地雷格）。玩家翻开一个非地雷格时，该格将会出现一个数字——提示周围格子中有多少个是地雷格。游戏的目标是在不翻出任何地雷格的条件下，找出所有的非地雷格。

现在给出 $n$ 行 $m$ 列的雷区中的地雷分布，要求计算出每个非地雷格周围的地雷格数。

注：一个格子的周围格子包括其上、下、左、右、左上、右上、左下、右下八个方向上与之直接相邻的格子。

** 输入格式**

第一行是用一个空格隔开的两个整数 $n$ 和 $m$，分别表示雷区的行数和列数。

接下来 $n$ 行，每行 $m$ 个字符，描述了雷区中的地雷分布情况。字符 $\text{*}$ 表示相应格子是地雷格，字符 $\text{?}$ 表示相应格子是非地雷格。相邻字符之间无分隔符。

** 输出格式**

输出文件包含 $n$ 行，每行 $m$ 个字符，描述整个雷区。用 $\text{*}$ 表示地雷格，用周围的地雷个数表示非地雷格。相邻字符之间无分隔符。

样例 #1

样例输入 #1

3 3
*??
???
?*?

样例输出 #1

*10
221
1*1

样例 #2

样例输入 #2

2 3
?*?
*??

** 样例输出 #2**

2*1
*21

提示

对于 $100\%$的数据，$1\le n\le 100,1\le m\le 100$。

#include<iostream>
using namespace std;

const int dx[]={-1,-1,-1,0,0,1,1,1};
const int dy[]={-1,0,1,-1,1,-1,0,1};
const int maxn=105;
char g[maxn][maxn];

int main( ){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>g[i][j];
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(g[i][j]!='*'){
                int cnt = 0;
                for(int k=0;k<=7;k++){
                    if(g[i+dx[k]][j+dy[k]]=='*')cnt++;
                }
                cout<<cnt;
            }else cout<<'*';
        }
        cout<<endl;
    }
        
    
    return 0;
}

[NOIP2016 提高组] 玩具谜题

题目背景

NOIP2016 提高组 D1T1

题目描述

小南有一套可爱的玩具小人, 它们各有不同的职业。

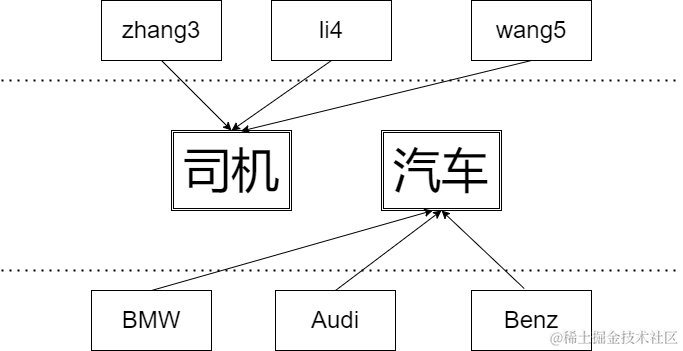
有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:

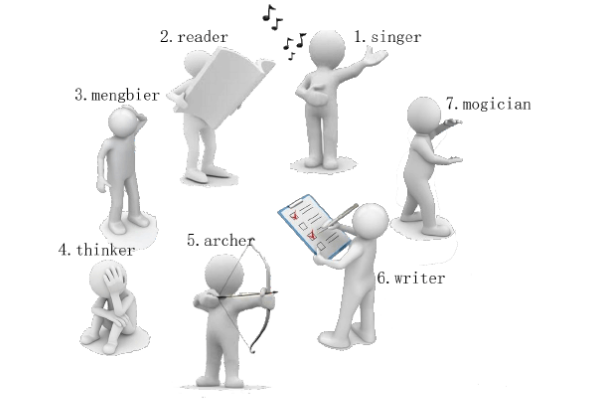
这时 singer 告诉小南一个谜題: “眼镜藏在我左数第 $3$ 个玩具小人的右数第 $1$ 个玩具小人的左数第 $2$ 个玩具小人那里。 ”

小南发现, 这个谜题中玩具小人的朝向非常关键, 因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人, 它的左边是顺时针方向, 右边是逆时针方向; 而面向圈外的玩具小人, 它的左边是逆时针方向, 右边是顺时针方向。

小南一边艰难地辨认着玩具小人, 一边数着:

singer 朝内, 左数第 $3$ 个是 archer。

archer 朝外,右数第 $1$ 个是 thinker 。

thinker 朝外, 左数第 $2$ 个是 writer。

所以眼镜藏在 writer 这里!

虽然成功找回了眼镜, 但小南并没有放心。 如果下次有更多的玩具小人藏他的眼镜, 或是谜题的长度更长, 他可能就无法找到眼镜了。所以小南希望你写程序帮他解决类似的谜题。 这样的谜題具体可以描述为:

有 $n$ 个玩具小人围成一圈, 已知它们的职业和朝向。现在第 $1$ 个玩具小人告诉小南一个包含 $m$ 条指令的谜題, 其中第 $z$ 条指令形如“左数/右数第 $s$,个玩具小人”。 你需要输出依次数完这些指令后,到达的玩具小人的职业。

输入格式
输入的第一行包含两个正整数 $n,m$，表示玩具小人的个数和指令的条数。

接下来 $n$ 行，每行包含一个整数和一个字符串，以逆时针为顺序给出每个玩具小人的朝向和职业。其中 $0$ 表示朝向圈内，$1$ 表示朝向圈外。 保证不会出现其他的数。字符串长度不超过 $10$ 且仅由英文字母构成，字符串不为空，并且字符串两两不同。整数和字符串之间用一个空格隔开。

接下来 $m$ 行，其中第 $i$ 行包含两个整数 $a_i,s_i$，表示第 $i$ 条指令。若 $a_i=0$，表示向左数 $s_i$ 个人；若 $a_i=1$，表示向右数 $s_i$ 个人。 保证 $a_i$ 不会出现其他的数，$1\le s_i<n$。

输出格式

输出一个字符串，表示从第一个读入的小人开始，依次数完 $m$ 条指令后到达的小人的职业。

样例 #1

样例输入 #1

7 3
0 singer
0 reader
0 mengbier 
1 thinker
1 archer
0 writer
1 mogician 
0 3
1 1
0 2

样例输出 #1

writer

样例 #2

样例输入 #2

10 10
1 C
0 r
0 P
1 d
1 e
1 m
1 t
1 y
1 u
0 V
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4

样例输出 #2

y

提示

【样例1说明】

这组数据就是【题目描述】 中提到的例子。

【子任务】

子任务会给出部分测试数据的特点。 如果你在解决题目中遇到了困难, 可以尝试只解决一部分测试数据。

每个测试点的数据规模及特点如下表:

其中一些简写的列意义如下:

• 全朝内: 若为“√”, 表示该测试点保证所有的玩具小人都朝向圈内;

• 全左数:若为“√”,表示该测试点保证所有的指令都向左数,即对任意的 $1\le z\le m,a_i=0$;

• $s=1$：若为“√”,表示该测试点保证所有的指令都只数 $1$ 个,即对任意的 $1\le z\le m,s_i=1$;

职业长度为 $1$：若为“√”,表示该测试点保证所有玩具小人的职业一定是一个长度为$1$的字符串。

#include<iostream>
#include<string>

using namespace std;

const int maxn = 1e6+5;
struct node{
    int head;
    string name;
}a[maxn];

int n,m,x,y;

int main( ){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>a[i].head>>a[i].name;
    }
    int now=0;
    for(int j=0;j<m;j++){
        cin>>x>>y;
        if(a[now].head==0&&x==1)now = (now + y) % n;
        else if(a[now].head==1&&x==0) now = (now + y) % n;
        else if(a[now].head==1&&x==1) now = (now - y + n) % n;
        else now = (now - y + n) % n;
    }
    cout << a[now].name;
    return 0;
}

• 难度较高的模拟题
  • 猪国杀
  • 立体图
  • 杀蚂蚁
  • 琪露诺的冰雪小屋

高精度

A+B Problem

P1601 A+B Problem（高精）

题目描述

高精度加法，相当于 a+b problem，不用考虑负数。

输入格式

分两行输入。$a,b\le 10^{500}$。

输出格式

输出只有一行，代表 $a+b$ 的值。

样例 #1

样例输入 #1

1
1

样例输出 #1

2

样例 #2

样例输入 #2

1001
9099

样例输出 #2

10100

提示

$20\%$ 的测试数据，$0\le a,b\le 10^9$；

$40\%$ 的测试数据，$0\le a,b\le 10^{18}$。

P1303 A*B Problem

题目描述

给出两个非负整数，求它们的乘积。

输入格式

输入共两行，每行一个非负整数。

** 输出格式**

输出一个非负整数表示乘积。

样例 #1

样例输入 #1

1 
2

样例输出 #1

2

提示

每个非负整数不超过 $10^{2000}$。

[NOIP1998 普及组] 阶乘之和

题目描述

用高精度计算出 $S=1!+2!+3!+\cdots +n!$（$n\le 50$）。

其中 ! 表示阶乘，定义为 $n!=n\times (n-1)\times (n-2)\times \cdots \times 1$。例如，$5!=5\times 4\times 3\times 2\times 1=120$。

输入格式

一个正整数 $n$。

输出格式

一个正整数 $S$，表示计算结果。

样例 #1

样例输入 #1

3

样例输出 #1

9

提示

【数据范围】

对于 $100\%$ 的数据，$1\le n\le 50$。

【其他说明】

注，《深入浅出基础篇》中使用本题作为例题，但是其数据范围只有 $n\le 20$，使用书中的代码无法通过本题。

如果希望通过本题，请继续学习第八章高精度的知识。

#include <iostream>
#include <string>
#include <cstdlib>
#include <cstring>

using namespace std;

#define maxn 100

struct Bigint {
    int len, a[maxn];
    Bigint(int x = 0) {
        memset(a, 0, sizeof(a));
        for (len = 1; x; len++)
            static_cast<void>(a[len] = x % 10), x /= 10;
        len--;
    }
    int& operator[](int i) {
        return a[i];
    }
    void flatten(int L) {
        len = L;
        for (int i = 1; i <= len; i++) {
            a[i + 1] += a[i] / 10;
            a[i] %= 10;
            for (; !a[len];)
                len--;
        }
    }
    void print() {
        for (int i = max(len, 1); i >= 1; i--)
            printf("%d", a[i]);
    }
};

Bigint operator+(Bigint a, Bigint b) {
    Bigint c;
    int len = max(a.len, b.len);
    for (int i = 1; i <= len; i++)
        c[i] += a[i] + b[i];
    c.flatten(len + 1);
    return c;
}

Bigint operator*(Bigint a, int b) {
    Bigint c;
    int len = a.len;
    for (int i = 1; i <= len; i++)
        c[i] = a[i] * b;
    c.flatten(len + 11);
    return c;
}

int main() {
    Bigint ans(0), fac(1);
    int m;
    cin >> m;
    for (int i = 1; i <= m; i++) {
        fac = fac * i;
        ans = ans + fac;
    }
    ans.print();
    return 0;
}