关于回归和拟合,从它们的求解过程以及结果来看,两者似乎没有太大差别,事实也的确如此。从本质上说,回归属于数理统计问题,研究解释变量与响应变量之间的关系以及相关性等问题。而拟合是把平面的一系列点,用一条光滑曲线连接起来,并且让更多的点在曲线上或曲线附近。更确切的说,拟合是回归用到的一种数学方法,而拟合与回归的应用场合不同。
拟合常用的方法有最小二乘法、梯度下降法、高斯牛顿(即迭代最小二乘)、列-马算法。其中最最常用的就是最小二乘法。并且拟合可以分为线性拟合与非线性拟合,非线性拟合比较常用的是多项式拟合。根据自变量的个数,拟合也可以分为曲线拟合与曲面拟合等。
回归大多数采用最小二乘法。回归可以分为一元线性回归、一元非线性回归、多元线性回归、多元非线性回归等。
1、最小二乘法
无论是在高等数学、线性代数,还是数理统计,我们都可以看到最小二乘法的身影。只不过每一部分侧重点不同,最终是殊途同归的。但是建议用矩阵的方法来做,这样很便于理解,计算起来也很方便。
最小二乘法的基本思路是:确定函数f(x),使得各个点x1,x2..xn处的函数值偏差f(x1)-y1、f(x2)-y2...f(xn)-yn的平方和或绝对值和最小。如果是一元线性拟合(回归),我们可以设方程为f(x)=kx+b。
这时我们求得函数值偏差平方和为。为了求它的最小值,利用高数的方法,就可以使M分别对k和b的偏导为0,最终求解得方程组:
公式1 :
公式2 :
由式2括号内为0,则有b的表达式
公式3 :
将式(3)代入到式(2)中得到式(4)
公式4 :
整理式(4)我们可以得到k的表达式
公式5 :
如果用线性代数的角度来看其实矩阵表达更加简洁,我们最终需要寻找最佳的k和b :
公式6 :
写成矩阵的形式:
公式7 :
令 ,
,
我们可以写成矩阵形式:
公式8 :
我们要解K,这时候X如果是方阵那么自然的就可以左右两边同时乘X的逆,但是如果X不是方阵(行数大于列数),我们可以左右同乘以X的转置,转换为方阵再取逆(当然能取逆的前提是行列式不能为0),具体如下,求得的逆叫做伪逆:
公式9 : =>
=>
所以解得K的值:
公式10 :
2、matlab实现
现在有这么一组数据
| x | y |
|---|---|
| 0.1 | 1.7805 |
| 0.3 | 2.2285 |
| 0.4 | 2.3941 |
| 0.75 | 3.2226 |
| 0.9 | 3.5697 |
我们利用matlab进行绘制散点图查看一下
x=[0.1;0.3;0.4;0.75;0.9];
y=[1.7805;2.2285;2.3941;3.2226;3.5697];
plot(x,y,'o')
xlim([0,1]);
ylim([1.6,3.7]);
hold on;
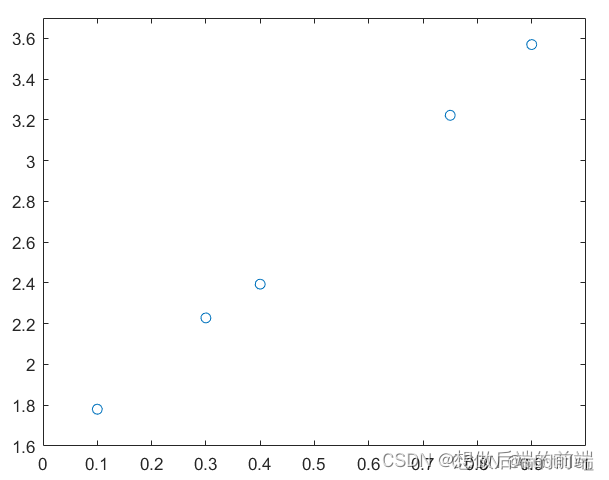
可以看出满足很好的线性关系,下面我们用上述最小二乘法的思想求一下拟合直线的k 和b :
方法1:代数方法计算
N=length(x);
k=(sum(y.*x)-N*mean(y)*mean(x))/(sum(x.^2)-N*mean(x)^2);
b=mean(y)-k*mean(x);
x_line=linspace(0,1,101);
y_line=k*x_line+b;
plot(x_line,y_line,'Color','r','LineWidth',1)
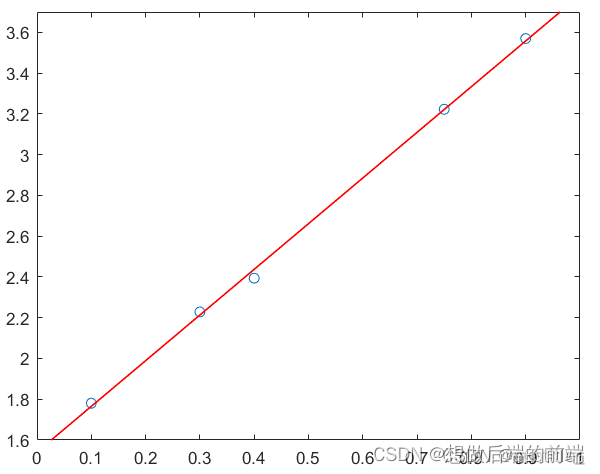
查看k和b的值:
k=2.2411
b=1.5409
方法2:矩阵计算
N=length(x);
X=[x,ones(N,1)];
Y=y;
K=inv(X'*X)*X'*Y;
k=K(1);
b=K(2);
x_line=linspace(0,1,101);
y_line=k*x_line+b;
plot(x_line,y_line,'Color','r','LineWidth',1)
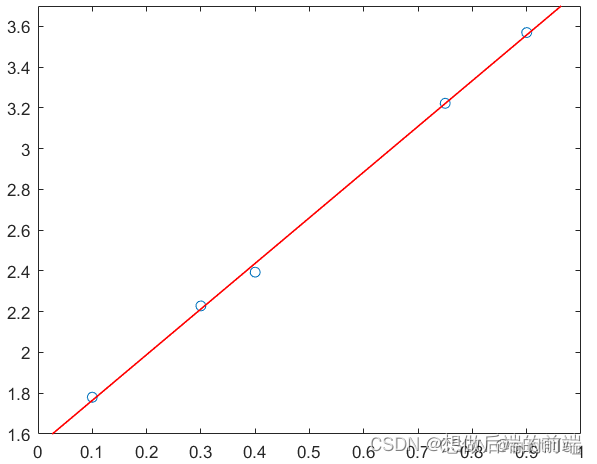
查看k和b的值:
k=2.2411
b=1.5409
至此,我们可以看到两种方法的结果是一样的。