代码随想录算法训练营第四十三天 | LeetCode 518. 零钱兑换 II、377. 组合总和 Ⅳ
文章链接:完全背包理论基础 零钱兑换 II 组合总和 Ⅳ
视频链接:完全背包理论基础 零钱兑换 II 组合总和 Ⅳ
1. 完全背包理论基础
1.1 思路
-
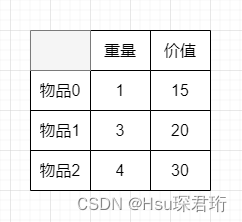
完全背包和 01 背包的区别就是,完全背包的物品可以取无数次,也是给我们一个背包,装满之后看最大价值是多少,01 背包的物品只能取 1 次。根据背包的特性,其中的区别只体现在遍历顺序上,因此其他几步就简写了。
-
确定 dp 数组及其下标的含义:dp[j] 表示容量为 j 的背包,所背的物品的最大价值为 dp[j]
-
递推公式:dp[j]=Math.max(dp[j],dp[j-weight[i]】+value[i])
-
dp 数组的初始化:dp[0] 表示背包容量为 0 的最大价值,就是 0 ,因为没有物品的重量为 0 可以放入背包中;非 0 下标,看递推公式 dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i])也是初始化时就应该把它初始化为非负数里的最小值即可,也就是 0
-
遍历顺序:因为我们之前的两层 for循环是先物品后背包,背包这一层是倒序遍历,为的就是让物品只使用一次,而我们现在可以无限使用,因此背包这一层就改为正序遍历。即 for(int i=0;i<weight.length();i++)for(int j=weight[i];j<=bagWeight;j++)bagWeight 就是背包的容量。
-
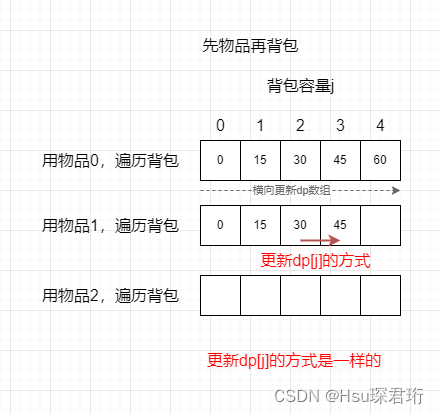
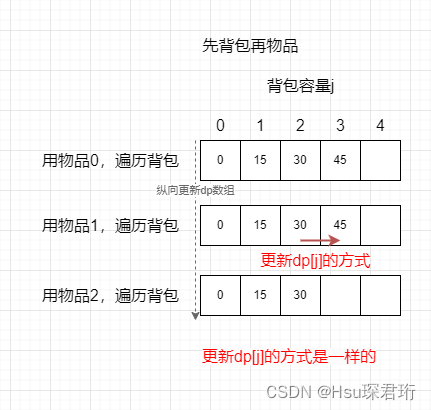
其实这里遍历顺序是先物品后背包,这里是可以颠倒的,可以先背包再物品。颠倒后是先确定了背包的容量再挨个放物品,从列上往下加物品,而先物品再背包则是从行上往右加物品,而我们的递推公式的第 i 个物品的 dp[j] 依赖的都是左边的 dp[j-1]dp[j-2] 这些值,而无论是从上往下还是从左往右,左边的 dp[j-1]dp[j-2] 永远有值,因此颠倒顺序是可以的。01 背包不可以是因为第 i 个物品的 dp[j] 依赖的是第 i-1 个物品的 dp 数组
-
打印 dp 数组:用于 debug
1.2 代码
//先遍历物品,再遍历背包
private static void testCompletePack(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){ // 遍历物品
for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
for (int j = 0; j < weight.length; j++){ // 遍历物品
if (i - weight[j] >= 0){
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
}
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
2. LeetCode 518. 零钱兑换 II
2.1 思路
- 本题和纯完全背包不同,纯完全背包求的是凑成背包的最大价值,本题求的是凑成总金额的组合数,注意是组合数,即 [2,1,2] 和 [2,2,1] 是一样的。这题和494. 目标和有点类似都是给一些物品和一个集合,问装满这个集合有多少种方法,和本题的区别是那题的物品只能用一次,本题的物品可以用无数次,因此那题是 01 背包,本题是完全背包
- dp 数组及其下标的含义:装满背包容量为 j 的背包有 dp[j] 种方法。最终求的是 dp[amount]
- 递推公式:就是我们放 i 个物品所对应的有多少种方法进行累加,即 dp[j]+=dp[j-coins[i]]。
- dp 数组的初始化:dp[0]=1,因为递推公式的通过前一个累加的,因此第一个不能为 0,为 0 就后面全是 0 了。dp[0] 的含义就是装满背包容量为 0 的方法有 1 种,空集也是一个集合。非 0 下标就是都是 0 即可,因为我们是累加的,为 0 就不会影响递推公式
- 遍历顺序,在上面纯完全背包上说了物品和背包的遍历顺序是可以颠倒的,但在本题就有点要求了,因为纯完全背包求的是装满后的最大价值,本题求的是装满后的最大组合数,而且还是组合,因此对遍历顺序也就有要求了。我们是先物品再背包 for(int i=0;i<coins.length;i++)for(int j=coins[i];j<=amonut;j++),dp[j]+=dp[j-coins[i]]背包这一层是正序遍历,因为物品可以使用无数次。而如果先背包后物品,就是物品在后,就会遍历多轮,从而出现重复组合的情况,如果物品在前,物品只遍历了一轮,因此本题不能颠倒顺序,求组合数就先物品再背包,求排列数就是先背包再物品。
- 打印 dp 数组:用于 debug
2.2 代码
class Solution {
public int change(int amount, int[] coins) {
//递推表达式
int[] dp = new int[amount + 1];
//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装
dp[0] = 1;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}
}
3. LeetCode 377. 组合总和 Ⅳ
3.1 思路
- 本题问用数组里的数凑成 target 有多少种方法,数组里的数可以使用无限次,因此是完全背包。本题求出的集合是讲究顺序的,也就是排列而不是组合,这题和518. 零钱兑换 II很相似,只是本题是求排列的,因此本题的动规五步曲其实就遍历顺序不一样,其他都是一样的,下面就简写了。
- dp 数组及其下标的含义:装满背包容量为 j 的背包有 dp[j] 种方法。最终求的是 dp[target]
- 递推公式:就是我们放 j 个物品所对应的有多少种方法进行累加,即 dp[i]+=dp[i-nums[j]]。
- dp 数组的初始化:dp[0]=1。非 0 下标就是都是 0 即可。
- 遍历顺序:在518. 零钱兑换 II说过了先物品再背包得到的是组合数,先背包再物品得到的是排列数,因为先背包再物品,物品在第二层循环里是每次都从开始往后取的,因此每次都能遍历多轮,因此得到的是排列数。举个例子:先物品再背后时计算 dp[4] 时只会出现 [1,3] 而不会出现 [3,1],因为是先物品再背包,3 是在 1 后面的,因此不会在 3 后面再出现 1 了。
- 打印 dp 数组:用于 debug
- 总结一下完全背包问题:对于纯完全背包,即求装满后的最大价值是什么,或者问能不能装满这个背包,那么两层 for 循环颠倒是可以的。但对完全背包问装满这个背包有多少种方法时就要区分是求的是组合数还是排列数,如果是组合数就是先物品再背包,如果是排列数就是先背包再物品
3.2 代码
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target + 1];
dp[0] = 1;
for (int i = 0; i <= target; i++) {
for (int j = 0; j < nums.length; j++) {
if (i >= nums[j]) {
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
}
}