题目难度: 困难
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给定一个二叉树的根节点 root ,返回其 最大路径和,即所有路径上节点值之和的最大值。
示例 1:
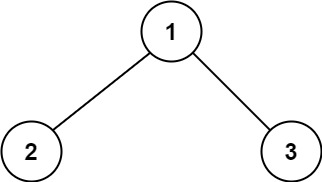
- 输入:root = [1,2,3]
- 输出:6
- 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
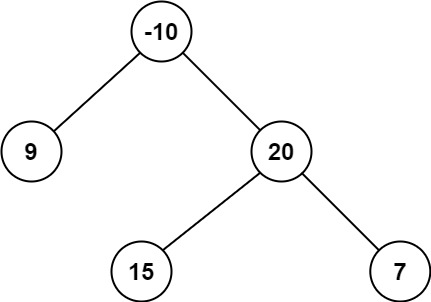
- 输入:root = [-10,9,20,null,null,15,7]
- 输出:42
- 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是 [1, 3 * 10^4]
- -1000 <= Node.val <= 1000
题目思考
- 最大路径和可能有哪些情况?
解决方案
思路
- 根据题目描述, 最大路径和无外乎两种情况: 1) 经过根节点; 2) 不经过根节点
- 我们先来考虑经过根节点的情况, 这里又包含几种可能性:
- 只包含根节点自身 (左右子树的路径和都是负值时)
- 左子树<->根
- 右子树<->根
- 左子树<->根<->右子树
- 以上几种情况的最大值, 就是经过根节点的最大路径和
- 而对于不经过根节点的情况, 它一定会经过某个子树的根节点, 这样就可以同样利用刚才的分析了
- 具体实现时, 我们可以利用 DFS, 传入当前节点, 然后返回以当前节点为根的子树的单向最大路径和 (也就是除了情况 4)
- 这样在处理它的父节点时, 就可以利用得到的返回值, 计算以父节点为根的子树的单向最大路径和了
- 这样一直递归下去, 就可以得到情况 1~3 的所有可能路径的最大值了
- 上面之所以返回子树的单向最大路径和, 而不包含情况 4, 是因为那样的话, 父节点就不能利用子节点的返回值来计算了, 以题目的示例 2 为例:
- 对于节点 20 所在的子树, 其情况 4 对应的路径是 15<->20<->7
- 如果我们的返回值也考虑它, 那么在处理节点-10 时, 它的右子树对应的最大路径就是 15<->20<->7
- 但该路径不能再加上节点-10 了, 因为那样会违反题目的要求: 同一个节点在一条路径序列中至多出现一次
- 所以子树返回的路径只能是单向路径, 不能是情况 4 那样, 穿过子树根节点
- 由于返回值只考虑了前三种情况, 所以我们需要额外维护一个全局最大路径和, 然后在遍历某个节点时, 将其对应的情况 4 也考虑进去, 这样最终遍历完成时, 那个全局最大路径和即为所求
- 下面代码中有详细的注释, 方便大家理解
复杂度
- 时间复杂度 O(N): 每个节点只会被遍历一次
- 空间复杂度 O(H): 递归调用最多使用 O(H) 栈空间, H 是树的高度
代码
class Solution:
def maxPathSum(self, root: TreeNode) -> int:
gmx = -float("inf")
def getSinglePathMaxSum(node):
# 返回以node为根的子树的单向路径最大和
nonlocal gmx
if not node:
return -float("inf")
# lmx和rmx分别是左右子树的单向路径最大和
lmx = getSinglePathMaxSum(node.left)
rmx = getSinglePathMaxSum(node.right)
# 求当前节点单向路径最大和, 注意它可能只包含当前节点自身 (例如左右子树路径和都是负数的情况)
# 注意单向路径不包含左子树+根+右子树的情况!!!
mx = max(node.val, lmx + node.val, rmx + node.val)
# 更新全局路径最大和gmx, 这里需要额外考虑左子树+根+右子树的路径
gmx = max(gmx, mx, lmx + rmx + node.val)
return mx
getSinglePathMaxSum(root)
return gmx
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊