【Hydro】不同潜在蒸散发计算方法说明

news2024/11/27 8:32:13

一、基本概念说明
- 蒸发 $E$ 、散发 $T$ 、蒸散发 $ET$
- 潜在蒸散发 $ET_p$ 、参考作物蒸散发 $ET_0$ 、实际蒸散发 $ET_a$ 及作物实际蒸散发 $ET_c$
二、部分潜在蒸散发估算方法表
三、SWAT模型中的潜在蒸散发计算
- Penman-Monteith法
- Priestley-Taylor法
- Hargreaves法
四、气象干旱等级规范（GB/T 20481—2017）
- Thornthwaite方法
- Thornthwaite方法python代码
六、潜在蒸散发计算Python代码
读取文件
参考文献

一、基本概念说明

蒸发 $E$ 、散发 $T$ 、蒸散发 $ET$

蒸散发 Evapotranspiration 包括蒸发 Evaporation 和散发（或蒸腾） Transpiration。
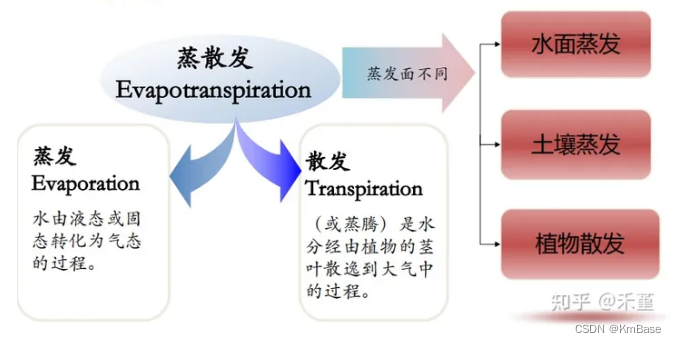
在这里插入图片描述

潜在蒸散发 $ET_p$ 、参考作物蒸散发 $ET_0$ 、实际蒸散发 $ET_a$ 及作物实际蒸散发 $ET_c$

蒸散发 $ET$ 是指水从地表蒸发并进入大气中的过程；
潜在蒸散发(Potential Evaportranspiration， $ET_p$ )亦称为可能蒸散发或蒸散发能力，简而言之，是指下垫面充分供水时的蒸散发；目前关于潜在蒸散发的定义还存在很大的分歧，不同学者根据不同的假设条件，提出了具有本质差别的定义。
参考作物蒸散发 $ET_0$ 则是指假设作物冠层与大气之间连续充分通气的条件下，作物叶面蒸腾和棵间蒸发损失的总和；
实际蒸散发 $ET_a$ 则是指在农田中实际发生的蒸散发，而作物实际蒸散发 $ET_c$ 则是指作物实际发生的蒸散发。
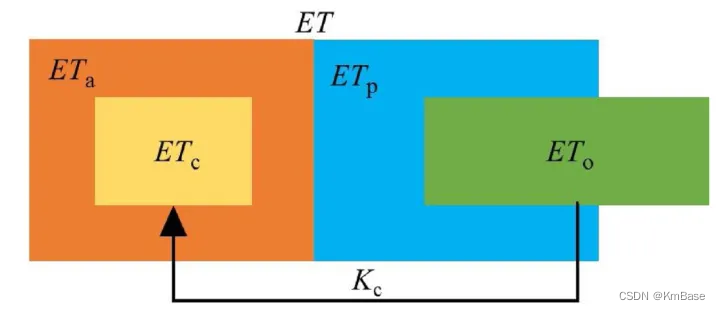
下图是几个相关概念的从属关系， $ET_a$ 、 $ET_c$ 、 $ET_p$ 、 $ET_0$ 都是ET的次级概念，其中 $ET_p$ 和 $ET_0$ 都能与 $ET_a$ 产生关联，因此有一定的共性。而 $ET_c$ 是 $ET_a$ 的一部分，因为 $ET_c$ 将 $ET_a$ 的范围缩小至特定的作物，进而与林地等的 $ET_a$ 进行区分。
在这里插入图片描述

二、部分潜在蒸散发估算方法表

国际上估算潜在蒸散发的模型有近50种；分为温度法、质量传输法、辐射法、综合法四类；彭曼方法被证明在不同条件下准确估算潜在蒸散发的值；但该方法需要大量气象数据，受资料和数据精度限制。
下表为13 种估算潜在蒸散发的方法，其中有综合法( P - M 方法) 、4 种温度法、2 种质量传输法以及 6 种辐射法：
在这里插入图片描述

三、SWAT模型中的潜在蒸散发计算

SWAT模型中包括三种潜在蒸散发计算：Penman-Monteith法(Monteith, 1965; Allen, 1986; Allen et al.,1989),Priestley-Taylor法(Priestley and Taylor,1972)和Hargreaves法(Hargreaves and Samani,1985)。SWAT模型也可以读入用户采用其他方法计算的潜在蒸散发量。

SWAT模型中三种方法需要的输入项不同：Penman-Monteith法需要太阳辐射、气温、相对湿度和风速；Priestley-Taylor法需要太阳辐射、气温和相对湿度；Hargreaves法只需要气温。

Penman-Monteith法

在这里插入图片描述

Priestley-Taylor法

在这里插入图片描述

Hargreaves法

在这里插入图片描述

四、气象干旱等级规范（GB/T 20481—2017）

根据气象干旱等级规范，计算MI（相对湿润度指数）时，标准推荐两种方法计算潜在蒸散量，即Thornthwaite方法和FAO Penman-Monteith方法。其中，FAO Penman-Monteith方法计算误差小，但需要的气象要素多，Thornthwaite 方法计算相对简单，需要的气象要素少，但有一定的局限性。使用者请根据资料条件选择合适的计算方法。

在这里插入图片描述

Thornthwaite方法

以下是Thornthwaite方法介绍
在这里插入图片描述

Thornthwaite方法python代码

以下是摘自互联网，基于Thornthwaite方法的python计算代码
原始数据：
在这里插入图片描述

处理后的数据：
在这里插入图片描述

代码：

#!usr/bin/env python
# -*- coding:utf-8 -*-
"""
@author: Su
@file: calculateMI.py
@time: 2023/08/17
@desc:
"""
import pandas as pd
import numpy as np


df = pd.read_excel('processdata/lianxi/鄂尔多斯.xlsx')
df[df['temp']<0] = np.nan
ab = df.dropna(axis=0,how='all')

# 计算Hi
temp = ab.temp.values
T = np.power(temp/5,1.514)
Hi = pd.DataFrame(T)

# 创建一个新DataFrame放入分类好后的站点数据
df2 = pd.DataFrame(ab)
df2.insert(loc=7, column='Hi',value=Hi.values)
# 给站点分类
nameList1 = set(df2.name.values)


# 想将结果写入excel，需创建空的dataframe
df_all = pd.DataFrame(data=None)

for i in nameList1:
    # 进行站点遍历
    dfName = df2[df2['name'] == i]
    df3 = pd.DataFrame(dfName)
    # 分年求和
    nameList2 = set(df3.year.values)


    for j in nameList2:
        # 按年遍历
        dfYear = df3[df3['year'] == j]
        df4 = pd.DataFrame(dfYear)
        # 计算Hi的和
        H_sum = dfYear['Hi'].sum()
        df4.insert(loc=8, column='H_sum', value=H_sum)
        # 计算A值
        A = (6.75e-07)*np.power(H_sum,3) - (7.71e-05)*np.power(H_sum,2) + (1.792e-02)*H_sum + 0.49
        df4.insert(loc=9, column='A', value=A)
        # 提取temp、H_sum、A用于计算PET
        temp = df4.temp.values
        H_sum = df4.H_sum.values
        A = df4.A.values
        # 计算PET
        PET = 16 * np.power((10*temp)/H_sum,A)
        df4.insert(loc=10, column='PET',value=PET)
        df5 = pd.DataFrame(df4)
        # concat 合并有相同字段名的dataframe
        df_all = pd.concat([df_all, df5],ignore_index=True)

# 避免字段名重复写入，一般会做去重处理
data_list = df_all.drop_duplicates(keep='first')
# 写出数据
df_all.to_excel('processdata/lianxi/鄂尔多斯PET.xlsx', index=False)

六、潜在蒸散发计算Python代码

源代码下载：潜在蒸散发计算Python源代码
具体包括以下方法

ETBase
Abtew
Albrecht
BlaneyCriddle
BrutsaertStrickler
Camargo
Caprio
ChapmanAustralia
Copais
Dalton
DeBruinKeijman
DoorenbosPruitt
GrangerGray
Hamon
HargreavesSamani
Haude
JensenHaiseBasins
Kharrufa
Linacre
Makkink
Irmak
MattShuttleworth
McGuinnessBordne
Penman
PenPan
PenmanMonteith
PriestleyTaylor
Romanenko
SzilagyiJozsa
Thornthwait
Ritchie
Turc
Valiantzas

，测试数据集camels_aus测试数据集下载方法：
pip install camels_aus，使用代码下载读取数据集

from camels_aus.repository import CamelsAus, download_camels_aus
download_camels_aus(path=r"E:/Other/ET_Python/data") # 下载到指定目录

读取文件

repo = CamelsAus()
repo.load_from_text_files(r"E:/Other/ET_Python/data")
dataset = repo.data

参考文献

论潜在蒸散发、参考作物蒸散发、实际蒸散发及作物实际蒸散发之差异
计算潜在蒸散量PET的方法
伍海，等，变化环境下12种潜在蒸散发估算方法在不同干湿区的适用性
气象干旱等级规范（GB/T 20481—2017）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1169144.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！