一、动态规划
动态规划(DP)一词指的是一系列算法,这些算法可用于在给定环境的完美模型作为马尔可夫决策过程(MDP)的情况下计算最优策略。经典的DP算法在强化学习中具有有限的实用性,既因为其对完美模型的假设,也因为其巨大的计算费用,但它们在理论上仍然很重要。DP为理解其余部分所介绍的方法提供了必不可少的理论基础。事实上,所有这些方法都可以被视为尝试实现与DP相同的效果,只是计算量更少,并且不假设环境的完美模型。
我们通常假设环境是一个有限MDP。也就是说,我们假设其状态、动作和奖励集S、A(s)和R对于s∈S是有限的,其动态由概率p(s0,r|s,a)给出,对于所有s∈S,a∈A(s),r∈R和s0∈S+(S+是S加上一个终态,如果问题是离散的)。尽管DP思想可以应用于具有连续状态和动作空间的问题,但只有在特殊情况下才能获得精确解。对于具有连续状态和动作的任务获得近似解的常见方法是量化状态和动作空间,然后应用有限状态DP方法。后续介绍的方法适用于连续问题,并且是该方法的重要扩展。
动态规划(DP)以及强化学习(RL)的核心思想是使用价值函数来组织和构建寻找最佳策略的过程。我们将介绍如何使用DP计算价值函数。正如之前所讨论的,一旦我们找到了最优的价值函数v或q,它们满足Bellman最优方程,我们就可以轻松地获得最优策略。
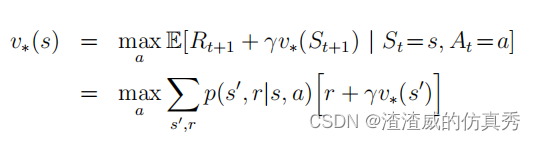
或者
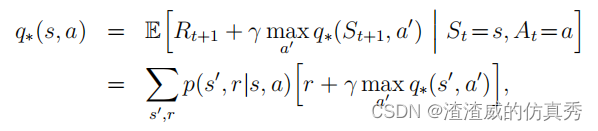
对于所有s∈S,a∈A(s)和s0∈S+,正如我们将看到的,DP算法是通过将Bellman等式转化为赋值来获得的,即将这些等式转化为更新规则,以改进所需价值函数的近似值。
二、策略评估
首先,我们来考虑如何计算任意策略π的状态值函数vπ。这在DP文献中被称为政策评估,也称为预测问题。我们可以得知,对于所有s∈S,
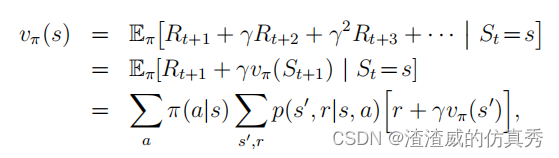
其中π(a|s)是在策略π下在状态s采取行动a的概率,并且期望值以π为下标,表示它们是条件于π被遵循。只要γ<1或从策略π下的所有状态保证最终终止,vπ的存在和唯一性就得到保证。
如果环境动态是完全已知的,那么上式就是|S|个同时线性方程的体系,需要解的是未知数(vπ(s), s∈S) |S|个。在原则上,它的解决方案虽然繁琐但却是直接的。对于我们的目的来说,迭代解法是最适合的。考虑一个近似值函数v0,v1,v2,...的序列,每个映射S+到R。初始近似值v0是任意选取的(除了终态,如果有的话,必须赋予值为0),每个连续的近似值都是通过使用作为更新规则的Bellman方程vπ来获得的:
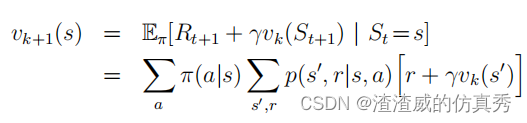
对于所有的s∈S。很明显,vk=vπ是这个更新规则的固定点,因为vπ的Bellman方程可以确保在这种情况下相等。事实上,序列{vk}在一般情况下可以证明当k→∞时收敛于vπ,这符合确保vπ存在的相同条件。这个算法被称为迭代政策评估。
为了从vk产生下一个近似值vk+1,迭代政策评估对每个状态s应用相同的操作:它将旧的状态s的值替换为从s的后继状态获得的新的值,以及在正在评估的政策下所有一步转移可能性的预期即时奖励。我们称这种操作为完全备份。每次迭代迭代政策评估都会备份每个状态的值一次,以产生新的近似值函数vk+1。根据被备份的对象是状态(如本例)还是状态-动作对,以及后继状态的估计值的组合方式不同,完全备份有几种不同的类型。所有在DP算法中进行的备份都称为完全备份,因为它们都是基于所有可能的后继状态,而不是基于样本后继状态。
三、实现的流程
要编写一个顺序计算机程序来实现迭代政策评估,如上式中所示,您需要使用两个数组,一个用于旧值vk(s),一个用于新值vk+1(s)。这样,可以从旧值逐个计算新值,而不会更改旧值。当然,使用一个数组并在原地更新值更容易,也就是说,每个新的备份值立即覆盖旧值。然后,根据状态被备份的顺序,有时上式右侧会使用新值而不是旧值。这个稍微不同的算法也会收敛到vπ;事实上,正如您所料,由于它使用新数据,通常比两个数组版本收敛得更快。我们认为备份是通过扫过状态空间来完成的。对于原地算法,在扫过过程中状态被备份的顺序对收敛速率有重要影响。当我们想到DP算法时,我们通常想到的是原地版本。
另一个实现问题涉及算法的终止。在形式上,迭代政策评估只在极限情况下收敛,但在实践中必须在达到极限之前停止。迭代政策评估的典型停止条件是在每次扫视后测试量 maxs∈S |vk+1(s) vk(s)| ,当它足够小时停止。图1给出了具有此停止标准的迭代政策评估的完整算法。

图1





![Verilog刷题[hdlbits] :Module cseladd](https://img-blog.csdnimg.cn/03ba5258302c457b9110b24128b120de.png)