题目描述
这是 LeetCode 上的 「117. 填充每个节点的下一个右侧节点指针 II」 ,难度为 「中等」。
Tag : 「BFS」、「链表」
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1: 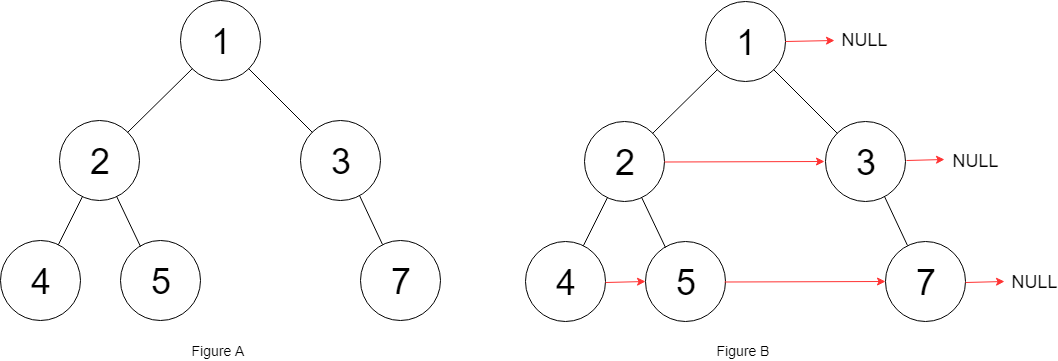
输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
示例 2:
输入:root = []
输出:[]
提示:
-
树中的节点数在范围 内 -
进阶:
-
你只能使用常量级额外空间。 -
使用递归解题也符合要求,本题中递归程序的隐式栈空间不计入额外空间复杂度。
BFS - 层序遍历
一个最直观的做法,是利用 BFS 对树进行「层序遍历」。
每个 BFS 回合中,对整层节点进行处理。
首先通过 pop 拿到当前节点,同时通过 peek 拿到当前层的下一节点,并建立 next 关系,注意需要跳过每层的最后一个节点。
Java 代码:
class Solution {
public Node connect(Node root) {
Node ans = root;
if (root == null) return ans;
Deque<Node> d = new ArrayDeque<>();
d.addLast(root);
while (!d.isEmpty()) {
int sz = d.size();
while (sz-- > 0) {
Node a = d.pollFirst();
if (sz != 0) a.next = d.peekFirst();
if (a.left != null) d.addLast(a.left);
if (a.right != null) d.addLast(a.right);
}
}
return ans;
}
}
C++ 代码:
class Solution {
public:
Node* connect(Node* root) {
Node* ans = root;
if (root == nullptr) return ans;
deque<Node*> d;
d.push_back(root);
while (!d.empty()) {
int sz = d.size();
while (sz-- > 0) {
Node* a = d.front();
d.pop_front();
if (sz != 0) a->next = d.front();
if (a->left) d.push_back(a->left);
if (a->right) d.push_back(a->right);
}
}
return ans;
}
};
Python 代码:
class Solution:
def connect(self, root: 'Node') -> 'Node':
ans = root
if root is None:
return ans
d = [root]
while d:
sz = len(d)
for i in range(sz):
a = d.pop(0)
if i != sz - 1:
a.next = d[0]
if a.left:
d.append(a.left)
if a.right:
d.append(a.right)
return ans
TypeScript 代码:
function connect(root: Node | null): Node | null {
let ans = root;
if (root == null) return ans;
const d = [root];
while (d.length > 0) {
let sz = d.length;
while (sz-- > 0) {
const a = d.shift() as Node;
if (sz != 0) a.next = d[0];
if (a.left) d.push(a.left);
if (a.right) d.push(a.right);
}
}
return ans;
};
-
时间复杂度: -
空间复杂度:
BFS - 逐层构建
上述解法中,每一层节点的 next 关系的构建都是独立的。我们构建第
层的 next 关系时,并没有利用已建好的到第
层的 next 关系。
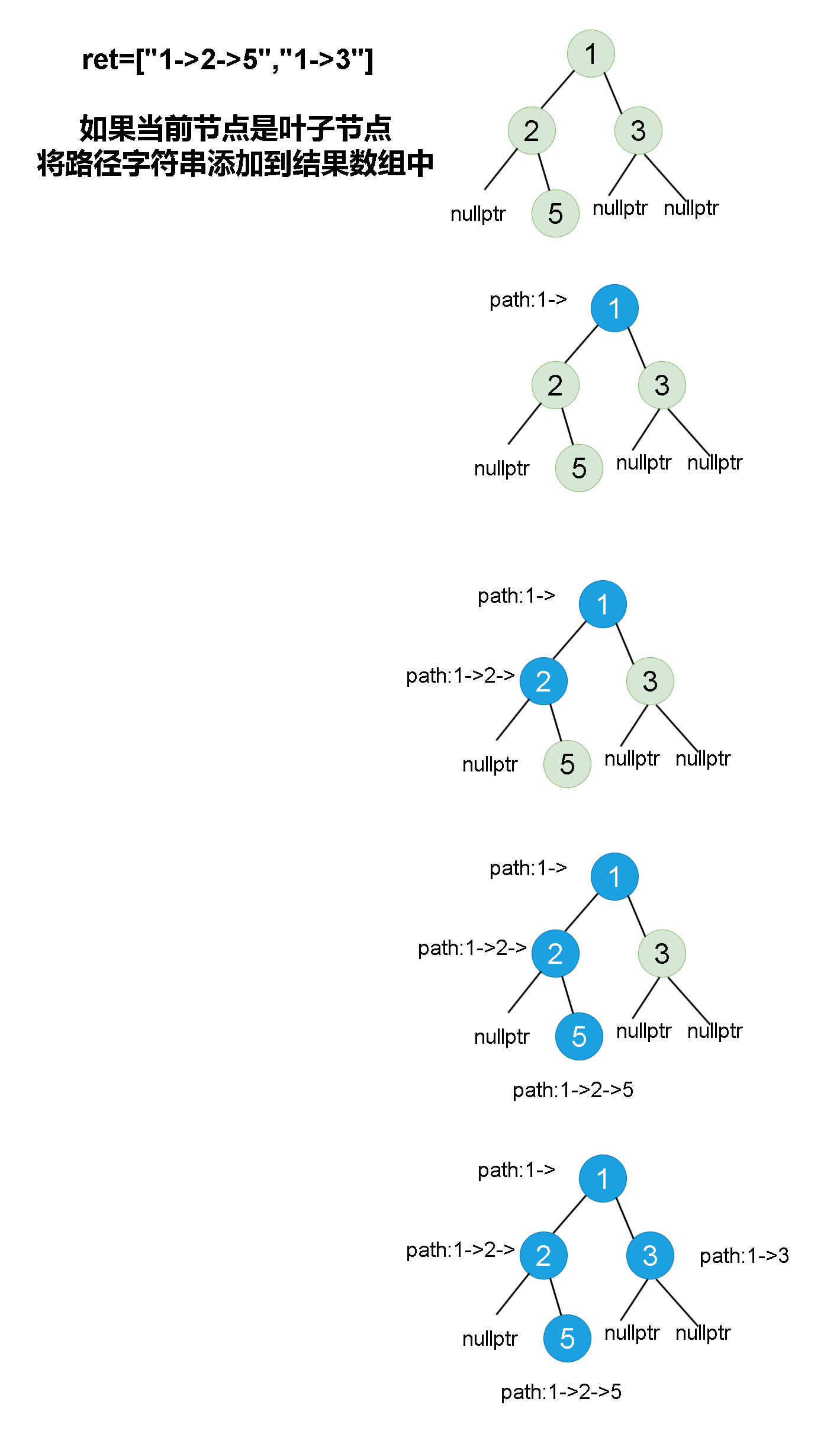
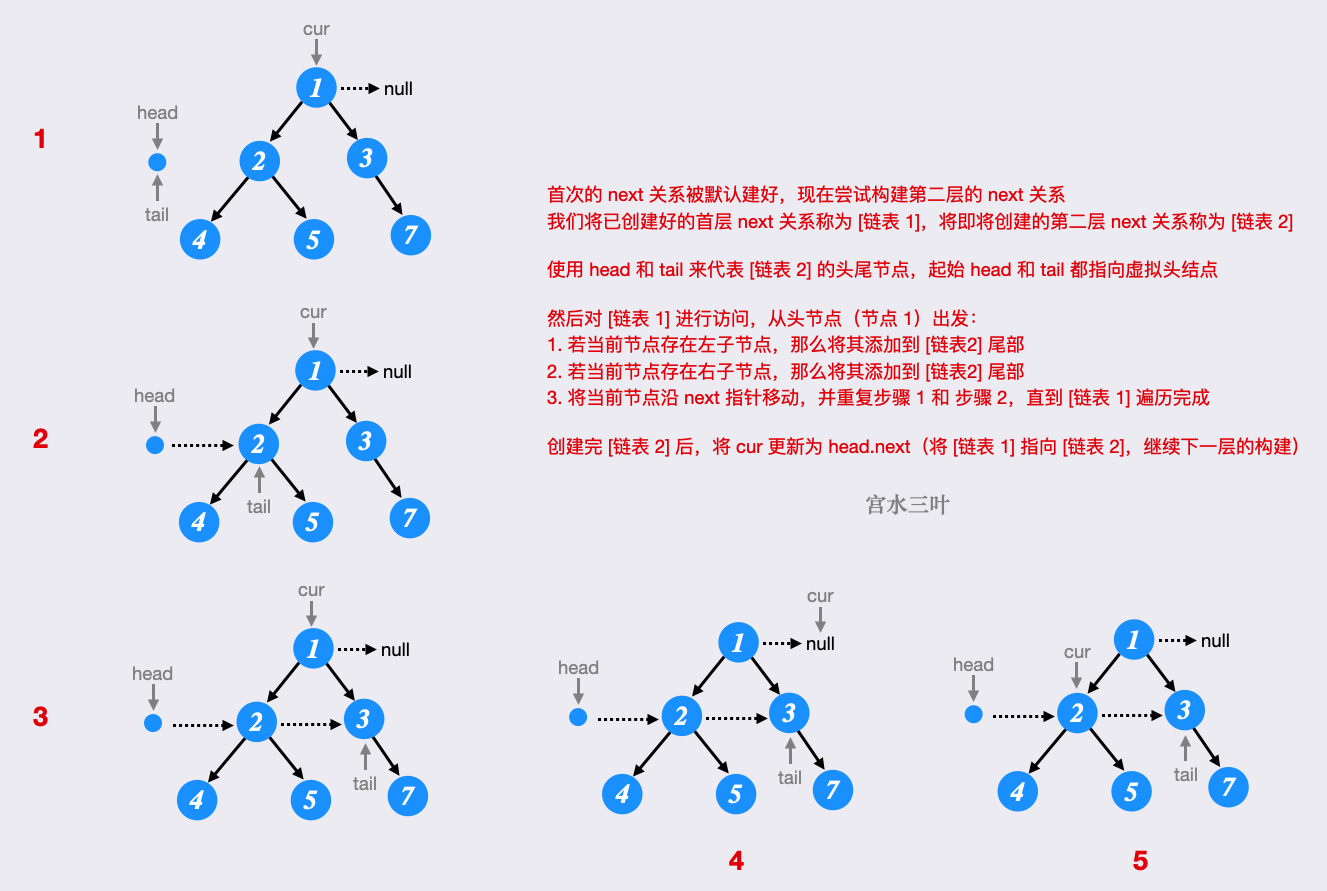
实际上,每一层构建好的 next 关系都可看做「链表」,可参与到下一层 next 关系的构建,同时由于所有节点的起始 next 指向都是 null,相当于首层的 next 关系已经默认建好了。
我们使用图解方式,来感受逐层构建过程:

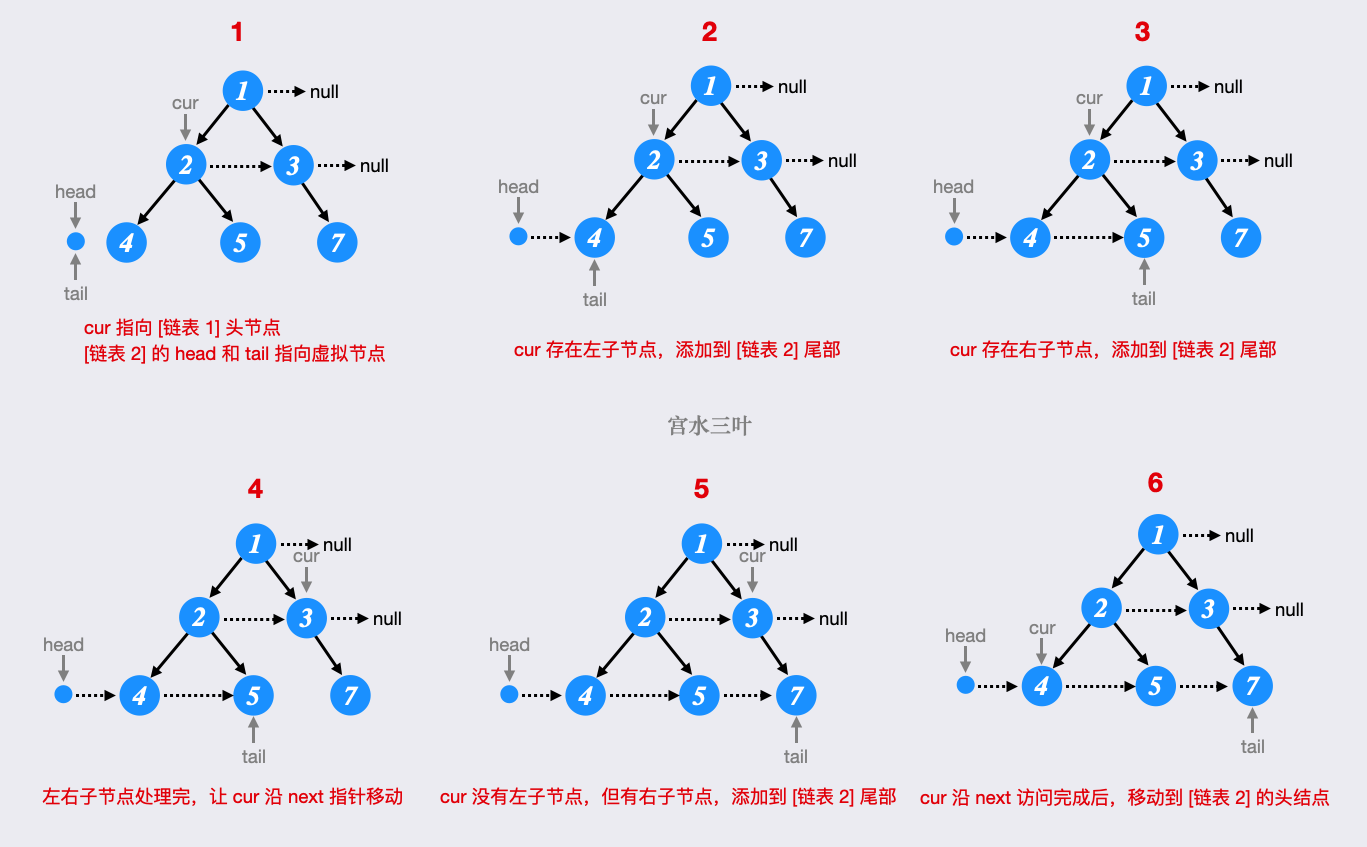
Java 代码:
class Solution {
public Node connect(Node root) {
Node ans = root;
if (root == null) return ans;
Node cur = root;
while (cur != null) {
Node head = new Node(-1), tail = head;
for (Node i = cur; i != null; i = i.next) {
if (i.left != null) tail = tail.next = i.left;
if (i.right != null) tail = tail.next = i.right;
}
cur = head.next;
}
return ans;
}
}
C++ 代码:
class Solution {
public:
Node* connect(Node* root) {
auto ans = root;
if (root == nullptr) return ans;
auto cur = root;
while (cur) {
auto head = new Node(-1), tail = head;
for (auto i = cur; i != nullptr; i = i->next) {
if (i->left) tail = tail->next = i->left;
if (i->right) tail = tail->next = i->right;
}
cur = head->next;
}
return ans;
}
};
Python 代码:
class Solution:
def connect(self, root: 'Node') -> 'Node':
ans = root
if not root:
return ans
cur = root
while cur:
head = Node(-1)
tail = head
i = cur
while i:
if i.left:
tail.next = i.left
tail = tail.next
if i.right:
tail.next = i.right
tail = tail.next
i = i.next
cur = head.next
return ans
TypeScript 代码:
function connect(root: Node | null): Node | null {
let ans = root;
if (root == null) return ans;
let cur = root;
while (cur != null) {
let head = new Node(-1), tail = head;
for (let i = cur; i != null; i = i.next) {
if (i.left) tail = tail.next = i.left;
if (i.right) tail = tail.next = i.right;
}
cur = head.next;
}
return ans;
};
-
时间复杂度: -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.117 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
本文由 mdnice 多平台发布