https://vjudge.net/contest/591700#problem/C

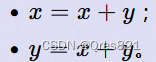
观察这个形式，如果交替做，就是个斐波那契数列

打表可得，任何正整数都可以大约由 $\log$ 个斐波那契数加起来

然后直接拼斐波那契数即可

#include<bits/stdc++.h>
using namespace std;
#ifdef LOCAL
 #define debug(...) fprintf(stdout, ##__VA_ARGS__)
#else
 #define debug(...) void(0)
#endif
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
#define fi first
#define se second
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
//#define N
//#define M
//#define mo
int n, m, i, j, k, T;
int f[100], mx, x, y; 
vector<pair<int, int> >v; 
vector<int>G[100]; 

void suan(int op) {
	if(op==1) ++x; 
	if(op==2) ++y; 
	if(op==3) x+=y; 
	if(op==4) y+=x; 
	debug("[%lld %lld]\n", x, y); 
}

void dfs(int x) {
	if(!x) {
		for(auto t : v) {
			debug("%lld %lld | %lld\n", mx, t.se, t.fi); 
			if(t.se%2) G[mx-t.se].pb(2); 
			else G[mx-t.se].pb(1); 
		}
		for(i=k=0; i<=mx; ++i) k+=G[i].size()+1; 
		printf("%lld\n", k); 
		for(i=0; i<=mx; ++i) {
			for(auto j : G[i]) {
				printf("%lld\n", j); suan(j); 
			}
			printf("%lld\n", (i%2 ? 3 : 4)); suan((i%2 ? 3 : 4)); 
		}
		return ; 
	}
	for(int i=90; i>=1; --i)
		if(x>=f[i]) {
			mx=max(mx, i); v.pb({f[i], i}); dfs(x-f[i]); 
			return ; 
		}
}

signed main()
{
	#ifdef LOCAL
	  freopen("in.txt", "r", stdin);
	  freopen("out.txt", "w", stdout);
	#endif
//	T=read();
//	while(T--) {
//
//	}
	n=read(); 
	f[0]=f[1]=1; 
	for(i=2; i<=90; ++i) f[i]=f[i-1]+f[i-2]; 
	dfs(n); 
	return 0;
}