目录
前言
赛题分析
1.问题一
问题分析
物料频率
代码详细操作:
出现频次
需求总数
趋势标量
方法
平均每天需求额度
整合代码
熵权法
详细介绍:
二、使用步骤
2.计算指标信息熵
3.熵权法相关代码
得到权重:
只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,有兴趣的小伙伴加我微信就好了。
我已经写到这么细化的份上了,求个大家的关注和点赞不过分吧!以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路,你们的关注和点赞就是我写作的动力!!!
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
前言
时间过去蛮久了还是有很多小伙伴加我微信想知道源代码哈,这里统一全部公布了。还有博主不是专业搞数学建模的哈,只是兴趣爱好,不包写论文和卖论文或者其他建模资料,关于E题小批量物料生产的所有解题和代码全部放到这篇帖子了哈,因为我还有工作所以没很多时间来写其他问题,也就写了第一题的详解,其他的解法参考我之前写的博文大体都是可以解决的,要是实在不行大家再私信我有时间我也做做看。
赛题分析
我们直接从赛题题目提出的问题来分析,进入赛题重述环节:
1.问题一
请对附件中的历史数据进行分析,选择 6 种应当重点关注的物料(可从物料需求出现的频数、数量、趋势和销售单价等方面考虑),建立物料需求的周预测模型(即以周为基本时间单位,预测物料的周需求量,见附录(1)),并利用历史数据对预测模型进行评价。
这里我们需要注意一下附件的说明:
-
将附件数据第 1 次出现的时间(2019 年 1 月 2 日)所在的周设定为第 1 周,以后的每周从周一开始至周日结束,例如,2019 年 1 月 7 日至 13 日为第 2 周,以此类推。
-
在制定本周的生产计划时,可以使用任何历史数据、需求特征以及预测数据,但不能使用本周及本周以后的实际需求数据。
-
服务水平 = 1 −缺货量/实际需求量 。
-
库存量和缺货量分别指物料在周末的库存量和缺货量。
再来看看附录数据:
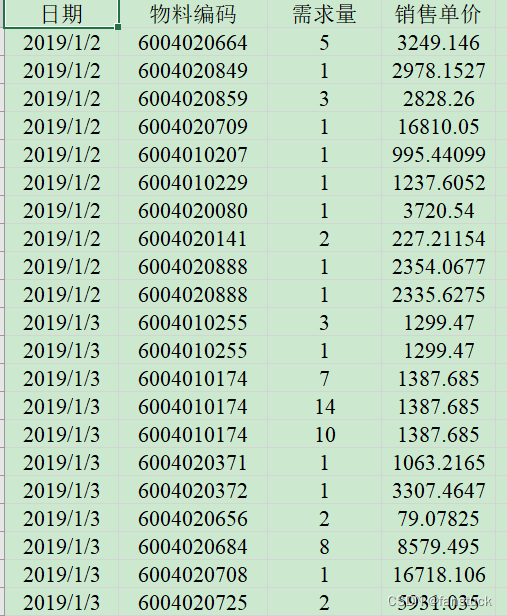
非常标准的时序数据,太好了我之前做时序预测模型正好缺乏此时序数据,这里正好可以拿来使用一下。那么根据上述信息我们来着手问题分析了。
问题分析
首先我们抓住题目的重点-选择 6 种应当重点关注的物料,注意括号里面的内容:
可从物料需求出现的频数、数量、趋势和销售单价等方面考虑
题目也是给的很明显,那么我们就根据这些指标来进行相应的分析:

我们发现总共有22453行数据,从19年1月2日星期一到22年5月21日,这里我们需要看一下日期:
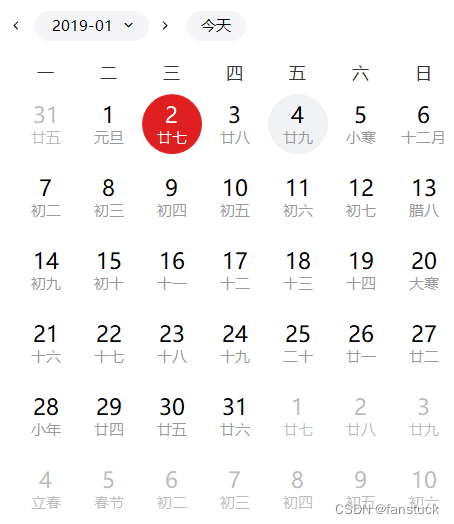
附件数据第 1 次出现的时间(2019 年 1 月 2 日)所在的周设定为第 1 周,那么也就是周三开始,到19年1月6日结束,这只有5天为第一周,与其他7天一周不同。再看22年5月21日:
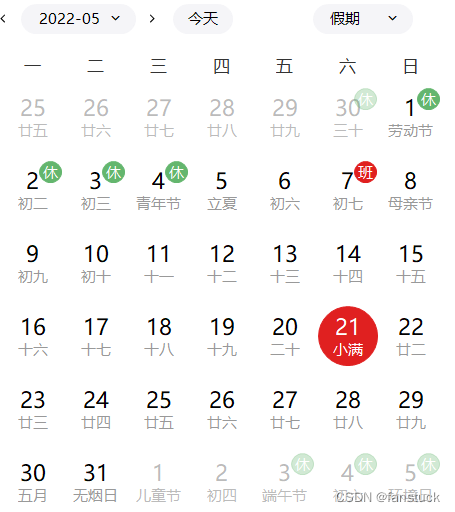
那么最后一周也只有16号道21号这6天,这需要注意一下,第一周的仅有五天,而最后一周只有6天。周期余留问题解决后,我们在来统计一下物料出现的频率:
物料频率
这个好解决,直接Pandas分析即可:

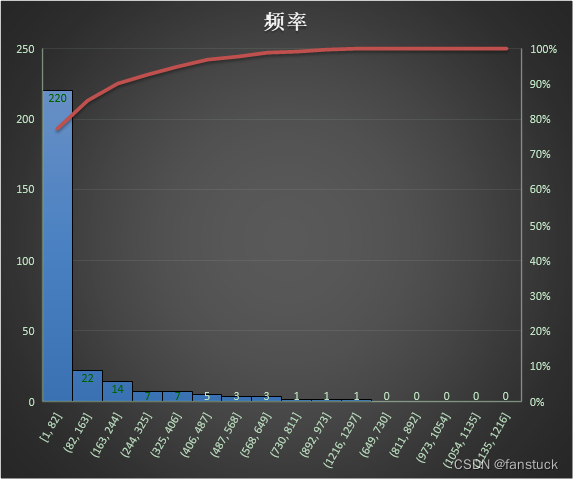
Pandas代码编写:
代码详细操作:
引入库:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
import math
from scipy.stats import norm
import statsmodels.api as sm
import time
import datetime
from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_score
from math import sqrt
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM,Dense,Dropout
from sklearn.model_selection import train_test_split
np.set_printoptions(suppress=True) # 取消科学计数法输出
#设置随机数种子
import tensorflow as tf
tf.random.set_seed(2)
plt.rcParams['font.sans-serif']=['Microsoft YaHei'] # 使用微软雅黑的字体
plt.style.use('ggplot')
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题很多库是可以不需要引入的,论文展示的话引入可以减少查重率
读入数据:
df_data=pd.read_excel(r'./附件.xlsx')
df_data_time=df_data.set_index('日期')ead_excel(rbf)rbf为路径:

聚合得到出现频次.
出现频次
df_group=df_data_time.groupby(by='物料编码')
se_group=df_group.size()
q1_1=se_group.head(10)
dict_q1_1 = {'物料编码':se_group.index,'出现频次':se_group.values}
df_q1_1=pd.DataFrame(dict_q1_1)
df_q1_1 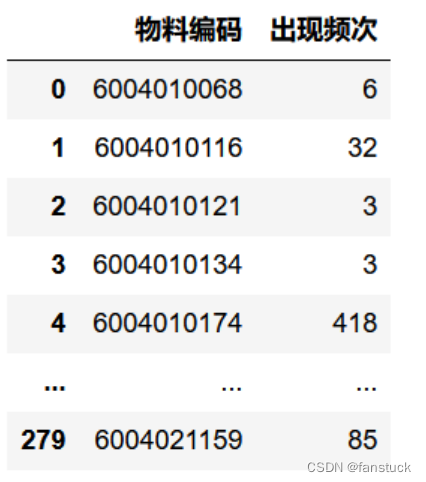

需求总数
需求量分析的话就更简单,我们需要进行聚合操作之后再排序,考虑总体需求量即可,当然也可以做的更细,将时间和频率结合起来,但是不需要,因为我们后续会整合统一考虑。
df_group_3=df_data_time.groupby(by='物料编码')
df_group_3_sum=df_group_3['需求量'].agg(['sum'])
#df_group_3_sum
q1_2=df_group_3_sum['sum'].sort_values(ascending=False).head(10)
se_q1_2=df_group_3_sum['sum']
dict_q1_2 = {'物料编码':se_q1_2.index,'需求总数':se_q1_2.values}
df_q1_2=pd.DataFrame(dict_q1_2)
df_q1_2 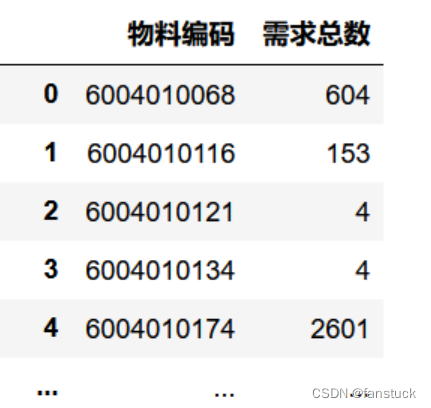

趋势标量
首先我们根据实际数据来思考,能够反应物料需求波动趋势的可以不用做的那么复杂,毕竟物料种类有283个,如果每个物料都去做一遍趋势分析的话,难免浪费太多时间,而且很多物料需求的发生频次只有一次或者两次,这极大的影响了判断。所以我们这里使用综合统计指标来评测。
方法
这里既然是趋势,那么我们完全可以使用sigmoid函数来实现一次归一化操作,将数据归一化后直接算出均值即可作为趋势指标。
早在一开始我就像将他们化为无量纲数据来分析趋势了,归一化数据之后融合了数据离散性,再根据均值比较仅得到他们的趋势即可,这样的话避免了需求量的数值影响从而得到更加精准的趋势标量。我们只需要选择标量趋于更大即可,这说明了我们需求量在逐渐增大,更加符合重要物料的性质。
def sigmoid_function(z):
fz = []
for num in z:
fz.append(1 / (1 + math.exp(-num)))
return fz
def columns_convert_df(series):
convert_df={series.name:series}
df_rank=pd.DataFrame(convert_df)
df_rank=df_rank.reset_index(drop=True)
return df_rank
df_group_4=df_data_time.groupby(by='物料编码')
str1=[]
str2=[]
for date,df_date in df_group_4:
str1.append(date)
str2.append(np.mean(sigmoid_function(df_date['需求量'].values)))
#print(str1)
#print(str2)
dict_1={'物料编码':str1}
dict_2={'趋势标量':str2}
df_q_3=pd.concat([pd.DataFrame(dict_1),pd.DataFrame(dict_2)],axis=1)
df_q_3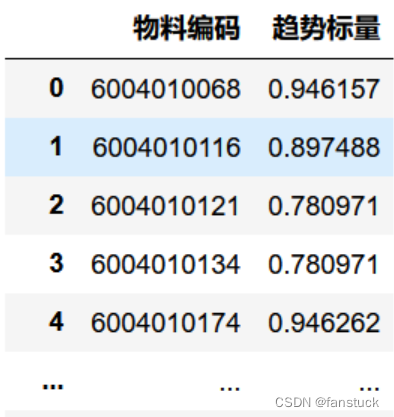
平均每天需求额度
这里可能有很多同学朋友想到销售单价那不肯定就是取个最低或者最高就好了嘛,你想想难道单价不是根据需求量来变化的?你单纯拿一个销售单价来分析,而不看需求量,就比如一个物料卖10,一个卖20就选取卖10块的,但是10块的物料只要20个,而卖20的需要30个呢?
我们来看看这个数据:
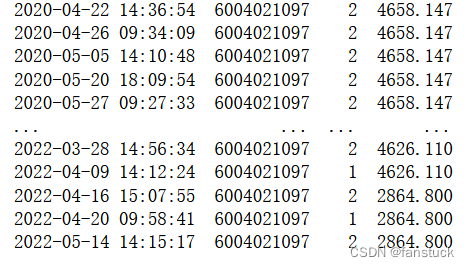
这一下就差了快2000了,但是如果你取他们的平均价格会损失相当多的信息。
而且根据数据观测我们也发现销售单价也是根据时间在波动所以我们完全可以根据上一个需求量的策略来进行分析,先将销售单价和需求量融合成成本指标:
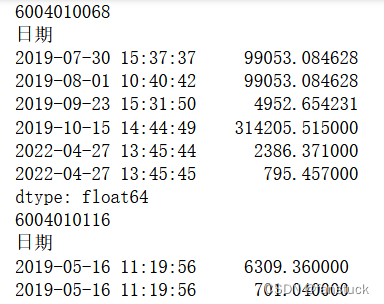
之后再根据聚合后的数据求一次平均从而得到平均每天需求额度,那么这个指标就融合和销售单价,当该指标越大时,说明该物料越值得关注:
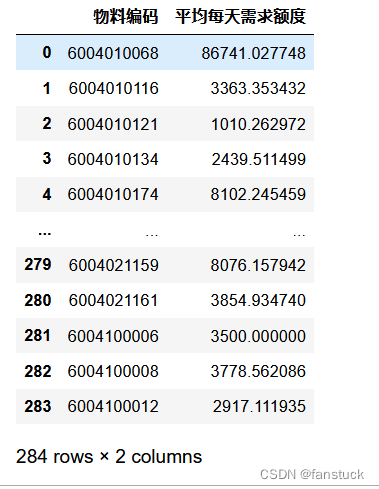
df_group_5=df_data_time.groupby(by='物料编码')
str_4=[]
for date,df_date in df_group_5:
df_4_money=df_date['需求量']*df_date['销售单价']
str_4.append(df_4_money.sum()/len(df_4_money))
dict_3={'平均每天需求额度':str_4}
df_q_4=pd.concat([pd.DataFrame(dict_1),pd.DataFrame(dict_3)],axis=1)
df_q_4 
整合代码
df_flow_1=pd.merge(df_q1_1,df_q1_2,how='outer',on='物料编码')
df_flow_2=pd.merge(df_flow_1,df_q_3,how='outer',on='物料编码')
df_flow_3=pd.merge(df_flow_2,df_q_4,how='outer',on='物料编码')
df_flow_3
熵权法
详细介绍:
在确定各项评价指标权重的算法中,熵权法在很多评价法作为计算指标权重的一只核心基础算法,如秩和比综合评价法RSR或是优劣解距离法TOPSIS。易于理解的话来讲,熵权法就是看该指标数据是否相对集中或是相对离散,要是基本上都差不多的数据,那么这些数据熵就很小,比较集中。说明在这个指标上面体现不出样本的差异性,导致这个指标并不是那么重要。所以该指标权重就小,相反数据差距很大,权重就大。
熵值法根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大, 该指标对综合评价的影响(即权重)就越大,如果某项指标的值全部相等,则该指标在综合评价中不起作用。因此,可利用信息熵这个工具,计算出各个指标的权重,为多指标综合评价提供依据。
二、使用步骤
1.数据预处理
拿到第一手数据后肯定不能直接使用的,需要进行数据预处理才能更好建模。
想对数据预处理方法了解更清楚的可以去看这篇:数据预处理归一化详细解释
这里我们使用数据处理方法之一的min-max标准化:
对于指标来说,一般分有正向指标和负向指标之分:
正向指标:指标值越大评价越好的指标,如脱单率,脱贫率。

负向指标:指标值越大评价越差的指标,如死亡率,失业率。

2.计算指标信息熵
(1)计算第项指标下第
个样本值占比重:

(2) 计算各指标的信息熵:
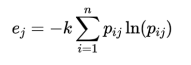 其中
其中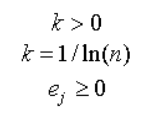
第项指标的数据差异越大,熵值越小;反之,熵值越大。
(3)计算信息效用值
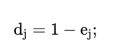
(4)计算指标权重
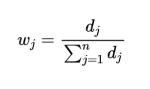
3.熵权法相关代码
data1=df_flow_3.iloc[:,1:]
data1_std=(data1-data1.min())/(data1.max()-data1.min())
m,n=data1_std.shape
data1_value=data1_std.values
k=1/np.log(m)
yij=data1_value.sum(axis=0)
#计算第j项指标下第i个样本值占比重:
pij=data1_value/yij
#计算各指标的信息熵:
test=pij*np.log(pij)
test=np.nan_to_num(test)
ej=-k*(test.sum(axis=0))
#计算每种指标的权重
wi=(1-ej)/np.sum(1-ej)
wi得到权重:

se_result_1=(df_flow_3['出现频次'].apply(lambda x: 1 / (1 + math.exp(-x))))*wi[0]
se_result_2=(df_flow_3['需求总数'].apply(lambda x: 1 / (1 + math.exp(-x))))*wi[1]
se_result_3=(df_flow_3['趋势标量'].apply(lambda x: 1 / (1 + math.exp(-x))))*wi[2]
se_result_4=(df_flow_3['平均每天需求额度'].apply(lambda x: 1 / (1 + math.exp(-x))))*wi[3]根据权重分别计算每个指标得分然后相加
觉大多数是出现在1-82的频次的,但是题目让我们选出六种那么我们需要综合考虑,我们可以进行排序将前10位的物料排名出来。

只希望各位以后遇到建模比赛可以艾特认识一下我,我可以提供免费的思路和部分源码,有兴趣的小伙伴加我微信就好了。
我已经写到这么细化的份上了,求个大家的关注和点赞不过分吧!以后的数模比赛只要我还有时间肯定会第一时间写出免费开源思路,你们的关注和点赞就是我写作的动力!!!
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
以上就是本期全部内容。我是fanstuck ,有问题大家随时留言讨论 ,我们下期见












![[普及练习场]失踪的7](https://img-blog.csdnimg.cn/c725ff95ac704efd868df586f3cff1a0.png)


