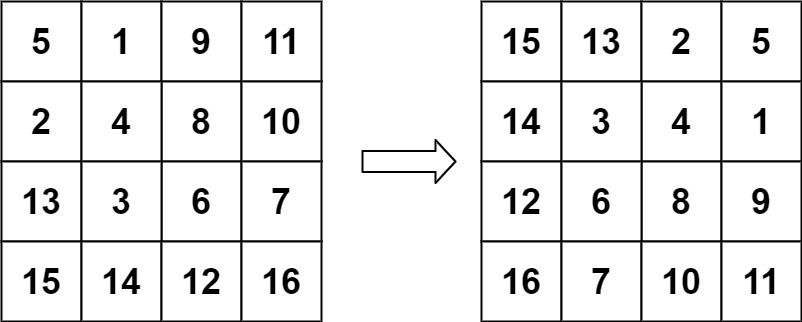
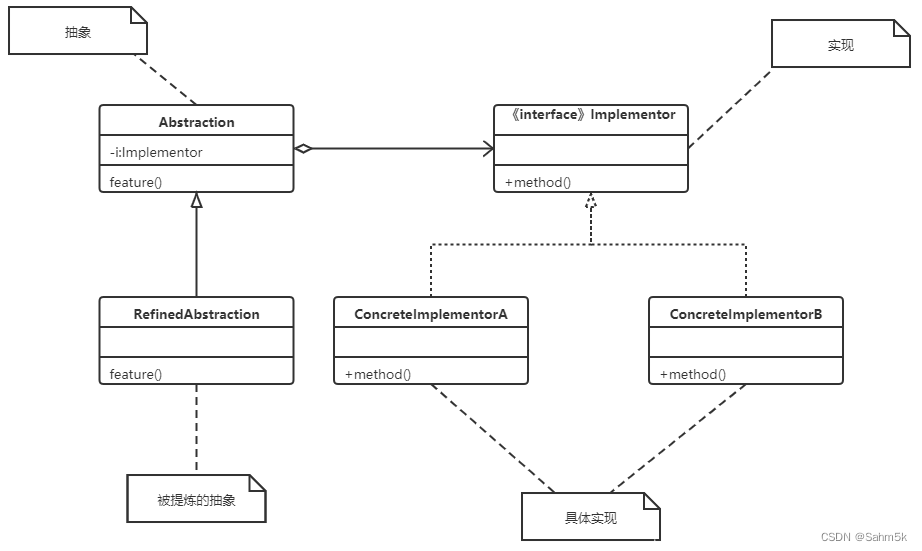
首先,借贷式拥塞控制 为什么能收敛到公平。sender 遵守算法约定的前提下给出一个原则和两个逻辑:
- 小 cwnd 的流在用大的但越来越小的 burst 率抢,大 cwnd 的流在用小的但越来越大的 burst 率让,最终达到平衡,不抢也不让。
- 如果当前流继续增加 inflight,它将继续降低 burst 率,即降低 pacing_rate,由于它增加了 inflight 而挤占了其它流的带宽,其它流在减少了带宽后将提高 burst 率,从而更容易将带宽抢回来(参考 插队原理),这构建了一个动态负反馈环。
- 参考 更合理的 bbr,时刻跟踪 E = bw / rtt,在其单调递增后开始减少时,记录拐点并认同上述第一点,在这附近进行微调。
因此,借贷式拥塞控制算法可以收敛到公平,并可以在最佳效能点收敛到公平,注意,我这里没有说最佳操作点,因为它不存在(最佳 “操作” 点是不可操作的)。
其次,借贷式拥塞控制算法如何动态适应带宽变化。
先看收敛点附近的情形:

算法承认并且确实要占据一些 buffer,这些 buffer 对发现带宽变化至关重要:
- 当有流量退出腾出带宽,buffer 可立即挤压出更大 delivery rate 被 sender 感知从而增加 cwnd。
- 当有流量侵入,v < buffer_limit 不至于丢包,但 E = bw / rtt 减少,从而降低 cwnd 和 burst 率。
现在给出借贷式拥塞控制整体的几何图示:

只要调好(或者事先确定好)一套参数,比如 rtt(rtt 由上图平衡线的斜率乘以系数表示),带宽系数,无论多少条流都可随意进出,公平收敛。整个拥塞控制问题可以转为几何问题。
最后,以排队论说明借贷式拥塞控制的收敛平衡性,它可用时延和负载关系图表达(下图从下往上读):

正常情况下统计复用节点的 rtt/load 线不会像 rtt 理论上那般 “平折”,最佳 E 值本身就依赖 buffer,如上图底部所示。
通过分析得到一个凹形收敛结构而不是凸形,说明借贷式拥塞控制是一个平衡的算法:
- 固定 buffer 用量,无论 cwnd 多大,以 C - cwnd 量级(乘变量或系数)的固有 pacing_rate 发送即可,C 为最大 inflight 容量。
- 基于 inflight 守恒律,采用 pacing_rate 匹配而不是 cwnd 匹配的方式向最优点公平收敛。
总之用它调教你的算法就对了,我此前总是抱怨 bbr probe 会挤压带宽,但我并没有把握说当 deliver_rate < gain * pacing_rate 时将 probe 完全回退是合理的,因为还要考虑到 n 退 1,n 非常大的场景,由排队理论知道这是一定要通过 buffer 重新分配带宽的,考虑到和 aimd 共存场景就更不能完全回退了,那么借贷式算法提供了另一个自平衡视角。
皮鞋没有蹬上,露着白袜子。
浙江温州皮鞋湿,下雨进水不会胖。