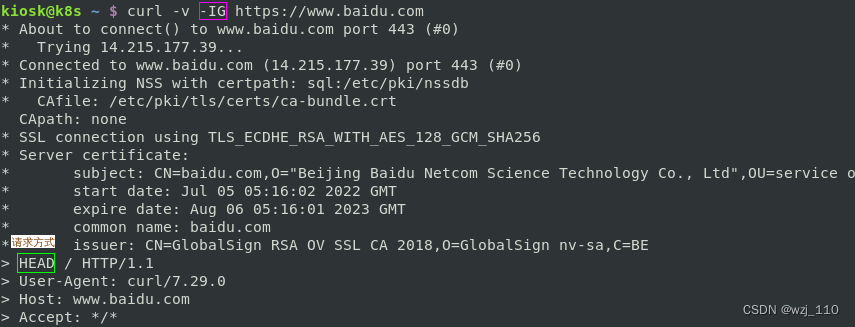
前一篇博客 《一文读懂滤波器的线性相位，全通滤波器，群延迟》 详细解释了线性相位滤波器，与之对应的是最小相位滤波器，本文就最小相位滤波器和线性相位滤波器进行比较。并提出问题： 线性相位滤波器一定更适合音频吗？ 先说结论：

1. 线性相位滤波器

• 优点：不影响相位
• 缺点：pre-ringing效应，听觉上类似chirp的效果。并且具有较高的延迟。

2. 最小相位滤波器

• 优点：延时低，相对于IIR对相位影响更小。
• 缺点：会带来相位的变化，只能用来补偿幅频响应，不能补偿相频响应。

1. 举例说明

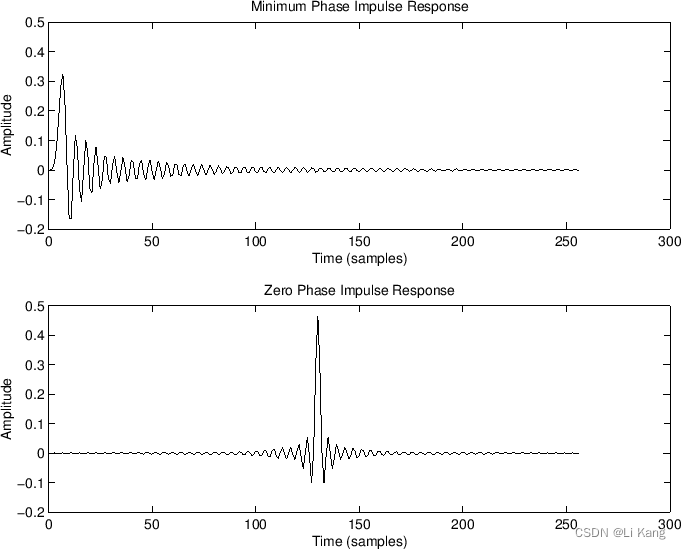
% ellipt.m - Compare minimum-phase and zero-phase
%            lowpass impulse responses.

dosounds = 1;
N = 8;     % filter order
Rp = 0.5;  % passband ripple (dB)
Rs = 60;   % stopband ripple (-dB)
Fs = 8192; % default sampling rate (Windows Matlab)
Fp = 2000; % passband end
Fc = 2200; % stopband begins [gives order 8]
Ns = 4096; % number of samples in impulse responses

[B,A] = nellip(Rp, Rs, Fp/(0.5*Fs), Fc/(0.5*Fs)); % Octave
% [B,A] = ellip(N, Rp, Rs, Fp/(0.5*Fs)); % Matlab

% Minimum phase case:
imp = [1,zeros(1,Ns/2-1)]; % or 'h1=impz(B,A,Ns/2-1)'
h1 = filter(B,A,imp); % min-phase impulse response
hmp = filter(B,A,[h1,zeros(1,Ns/2)]); % apply twice

% Zero phase case:
h1r = fliplr(h1); % maximum-phase impulse response
hzp = filter(B,A,[h1r,zeros(1,Ns/2)]); % min*max=zp
% hzp = fliplr(hzp); % not needed here since symmetric
% elliptplots; % plot impulse- and amplitude-responses

% Let's hear them!
while(dosounds)
  sound(hmp,Fs);
  pause(0.5);
  sound(hzp,Fs);
  pause(1);
end

2. 最小相位定义

2.1 最小相位多项式

2.2 最大相位滤波器

对于一个稳定的线性时不变系统，如果它的所有零点都在单位圆外，则该系统被称为最大相位。最大相位的例子就是上一篇博客中提到的纯延迟和全通滤波器。

1. 纯延迟，传递函数为$H(z)=z^{-n}$，其所有极点都在$z=0$处，而零点都在$z=\infty$
2. 全通滤波器，传递函数为
   $$H(z)=\frac{c+z^{-1}}{1+c{z}^{-1}}$$ $$c=\frac{tan(\pi \ast fc/fs)-1}{tan(\pi \ast fc/fs)+1}$$其中fc为截止频率，fs为采样频率，其中参数$c$范围为 (-1.0,1.0)。因此所有的极点都在单位圆内，而所有零点都在单位圆外，是最大相位滤波器。

2.3 最小相位意味最快的衰减

2.4 最小相位/全通分解

3. 建立最小相位系统