梯度消失和梯度爆炸
梯度爆炸和梯度消失本质上是因为梯度反向传播中的连乘效应。
梯度下降算法
举一个简单的例子,函数表达式为loss = 2w^2 + 4w,如下图
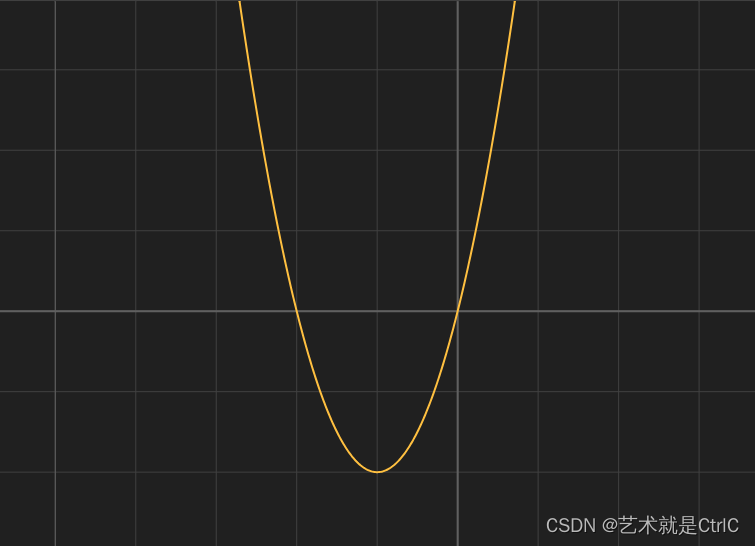
为了求得w的最优值,使得loss最小,从上图很容易看出来当w = -1时,loss最小,也就是当loss函数的导数为0时。
对w1随机取一个值,比如w1 = 0.5,此时
loss = 2 * 0.5^2 + 4 * 0.5 = 2.5, loss' = 4 * w1 + 4 = 4 * 0.5 + 4 = 6
如果我们把w1减少0.1,即w2 = 0.4,那么loss就会缩小0.1的5倍多不到6倍,此时
loss = 2 * 0.4^2 + 4 * 0.4 = 1.92, loss' = 4 * w2 + 4 = 4 * 0.4 + 4 = 5.6
于是经过多次迭代,当wn = -1,loss降到最小值,loss函数的导数此时也为0了
loss = -2, loss' = 4 * wn + 4 = 4 * -1 + 4 = 0
由此可见当我们缩小w的值,loss也会缩小,最终取得最优值,这就是梯度下降的目的。
复合函数
在深度学习训练中,实际问题往往不是一个简单的函数能够表达的,而是需要复合函数来作为映射方法。即已知函数y = f(u),当u表示为u = g(x)时,y作为x的函数就可以表示为y = f(g(x))这样的嵌套结构,这种嵌套结构的函数,就称为f(u),g(x)的复合函数。
例子:函数y = (2 - x)^2 是函数u = 2 - x 和函数y = u^2的复合函数
链式法则
已知函数y = f(u),函数u = g(x),复合函数y = f(g(x))的导函数可以表示为y' = dy/dx = (dy/du)*(du/dx)
在多层神经网络中,输入x,最后一层输出y4,损失函数为C,激活函数为S,可以列出
y1 = S(z1) = S(w1x + b1)
y2 = S(z2) = S(w2x + b2) = S(w2y1 + b2) (上一层的输出是这一层的输入)
y3 = S(z3) = S(w3x + b3) = S(w3y2 + b2) (同上)
y4 = S(z4) = S(w4x + b4) = S(w4y3 + b2) (同上)
根据链式法则,对b1求导得
dC/db1 = (dC/dy4)*(dy4/dz4)*(dz4/dy3)*(dy3/dz3)*(dz3/dy2)*(dy2/dz2)*(dz2/dy1)*(dy1/dz1)*(dz1/db1) = (dC/dy4)*S(z4)'*w4*S(z3)'*w3*S(z2)'*w2*S(z1)'*1
如果激活函数S为Sigmoid,则S'的函数曲线如下
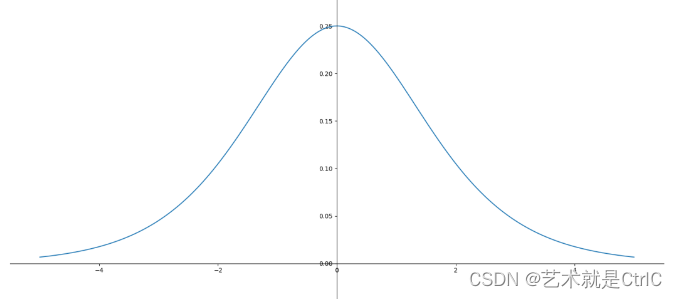
可以看到S'值域区间为[0,0.25],以最大值0.25代入上述例子,
即dC/db1 = (dC/dy4)*0.25*0.25*0.25*0.25*1
再代入梯度下降算法更新公式θ = θ0 - η*▽f(θ0),
即b1 = b1 - η*(dC/dy4)*0.25*w4*0.25*w3*0.25*w2*0.25*1
当神经网络层数足够多时,η*▽f(θ0)将会变得非常小,θ会更新得非常慢,即梯度消失。
又有如果初始权值w大于1甚至更大,导致θ更新过大,即梯度爆炸。