文章目录
- 简介
- 概念
- 随机变量与随机过程
- 马尔可夫链
- 隐含马尔可夫模型
- 两个基本假设
- 三个基本问题
- 算法
- 观测序列生成算法
- 概率计算算法
- 前向概率与后向概率
- 前向算法
- 后向算法
- 小结
- 概率与期望
- 学习问题
- 监督学习方法
- Baum-Welch算法
- 预测算法
- 近似算法(MAP)
- 维特比算法(Viterbi)
简介
-
动态贝叶斯网络的最简单实现隐马尔可夫模型。HMM可以看成是一种推广的混合模型。
-
序列化建模,打破了数据独立同分布的假设。
-
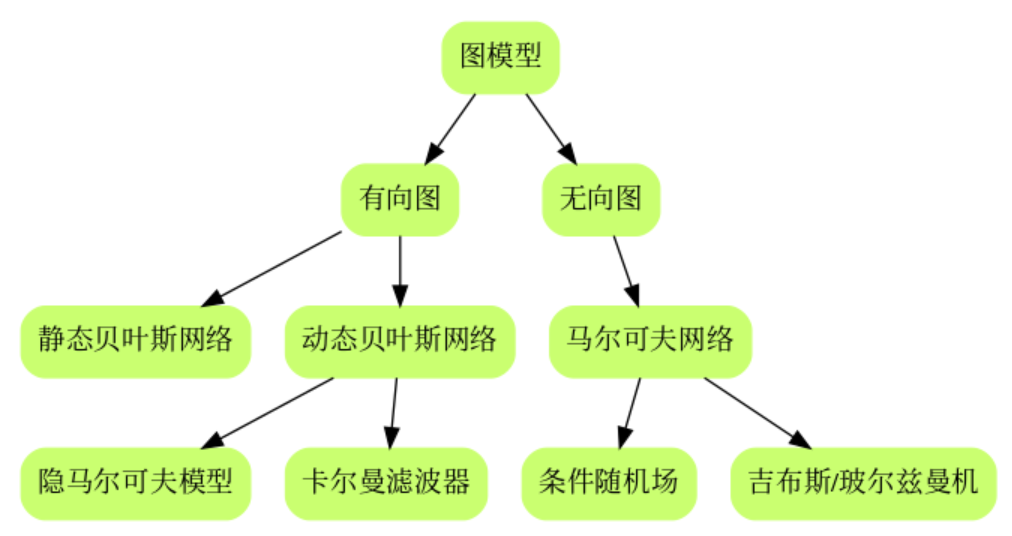
有些关系需要理清
-
另外一个图
另外,注意一点,在李老师这本书上介绍的HMM,涉及到举例子的,给的都是观测概率矩阵是离散的情况,对应了Multinominal HMM。但这个观测概率矩阵是可以为连续的分布的,比如高斯模型,对应了Gaussian HMM,高斯无处不在。具体可以参考hmmlearn库[^2]
- HMM有两个基本假设和三个基本问题, 两个基本假设。 I I I是隐变量。
概念
随机变量与随机过程
19世纪, 概率论的发展从对(相对静态的)随机变量的研究发展到对随机变量的时间序列 s 1 , s 2 , s 3 , … , s t , … s_1,s_2, s_3, \dots,s_t,\dots s1,s2,s3,…,st,…,即随机过程(动态的)的研究
马尔可夫链
随机过程有两个维度的不确定性。马尔可夫为了简化问题,提出了一种简化的假设,即随机过程中各个状态 s t s_t st的概率分布,只与它的前一个状态 s t − 1 s_{t-1} st−1有关, 即 P ( s t ∣ s 1 , s 2 , s 3 , … , s t − 1 ) = P ( s t ∣ s t − 1 ) P(s_t|s_1, s_2, s_3, \dots,s_{t-1})=P(s_t|s_{t-1}) P(st∣s1,s2,s3,…,st−1)=P(st∣st−1)
这个假设后来被称为马尔可夫假设,而符合这个假设的随机过程则称为马尔可夫过程,也称为马尔可夫链
P ( s t ∣ s 1 , s 2 , s 3 , … , s t − 1 ) = P ( s t ∣ s t − 1 ) P(s_t|s_1, s_2, s_3, \dots,s_{t-1})=P(s_t|s_{t-1}) P(st∣s1,s2,s3,…,st−1)=P(st∣st−1)
时间和状态取值都是离散的马尔可夫过程也称为马尔可夫链
隐含马尔可夫模型
P ( s 1 , s 2 , s 3 , … , o 1 , o 2 , o 3 , … ) = ∏ t P ( s t ∣ s t − 1 ) ⋅ P ( o t ∣ s t ) P(s_1,s_2,s_3,\dots,o_1,o_2,o_3,\dots)=\prod_tP(s_t|s_{t-1})\cdot P(o_t|s_t) P(s1,s2,s3,…,o1,o2,o3,…)=t∏P(st∣st−1)⋅P(ot∣st)
隐含的是状态 s s s
隐含马尔可夫模型由初始概率分布(向量 π \pi π), 状态转移概率分布(矩阵 A A A)以及观测概率分布(矩阵 B B B)确定.
隐马尔可夫模型
λ
\lambda
λ 可以用三元符号表示, 即
λ
=
(
A
,
B
,
π
)
\lambda = (A, B, \pi)
λ=(A,B,π)
其中 A , B , π A,B,\pi A,B,π称为模型三要素。
具体实现的过程中,如果观测的概率分布是定的,那么 B B B就是确定的。在hhmlearn中,实现了三种概率分布的HMM模型:MultinominalHMM,GaussianHMM,GMMHMM。还可以定义不同的emission probabilities[^3],生成不同的HMM模型。
两个基本假设
-
齐次马尔科夫假设(状态)
P ( i t ∣ i t − 1 , o t − 1 , … , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , … , T P(i_t|i_{t-1},o_{t-1},\dots,i_1,o_1) = P(i_t|i_{t-1}), t=1,2,\dots,T P(it∣it−1,ot−1,…,i1,o1)=P(it∣it−1),t=1,2,…,T
注意书里这部分的描述假设隐藏的马尔可夫链在任意时刻 t t t的状态 → i t \rightarrow i_t →it
只依赖于其前一时刻的状态 → i t − 1 \rightarrow i_{t-1} →it−1
与其他时刻的状态 → i t − 1 , … , i 1 \rightarrow i_{t-1, \dots, i_1} →it−1,…,i1
及观测无关 → o t − 1 , … , o 1 \rightarrow o_{t-1},\dots,o_1 →ot−1,…,o1
也与时刻 t t t无关 → t = 1 , 2 , … , T \rightarrow t=1,2,\dots,T →t=1,2,…,T
如此烦绕的一句话, 用一个公式就表示了, 数学是如此美妙.
-
观测独立性假设(观测)
P ( o t ∣ i T , o T , i T − 1 , o T − 1 , … , i t + 1 , o t + 1 , i t , i t − 1 , o t − 1 , … , i 1 , o 1 ) = P ( o t ∣ i t ) P(o_t|i_T,o_T,i_{T-1},o_{T-1},\dots,i_{t+1},o_{t+1},i_t,i_{t-1},o_{t-1},\dots,i_1,o_1)=P(o_t|i_t) P(ot∣iT,oT,iT−1,oT−1,…,it+1,ot+1,it,it−1,ot−1,…,i1,o1)=P(ot∣it)
书里这部分描述如下假设任意时刻 t t t的观测 → o t \rightarrow o_t →ot
只依赖于该时刻的马尔可夫链的状态 → i t \rightarrow i_t →it
与其他观测 → o T , o T − 1 , … , o t + 1 , o t − 1 , … , o 1 \rightarrow o_T,o_{T-1},\dots,o_{t+1},o_{t-1},\dots,o_1 →oT,oT−1,…,ot+1,ot−1,…,o1
及状态无关 → i T , i T − 1 , … , i t + 1 , i t − 1 , … , i 1 \rightarrow i_T,i_{T-1},\dots,i_{t+1},i_{t-1},\dots,i_1 →iT,iT−1,…,it+1,it−1,…,i1
三个基本问题
-
概率计算问题
输入: 模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π), 观测序列 O = ( o 1 , o 2 , … , o T ) O=(o_1,o_2,\dots,o_T) O=(o1,o2,…,oT)
输出: P ( O ∣ λ ) P(O|\lambda) P(O∣λ) -
学习问题
输入: 观测序列 O = ( o 1 , o 2 , … , o T ) O=(o_1,o_2,\dots,o_T) O=(o1,o2,…,oT)
输出: 输出 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π) -
预测问题, 也称为解码问题(Decoding)
输入: 模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π), 观测序列 O = ( o 1 , o 2 , … , o T ) O=(o_1,o_2,\dots,o_T) O=(o1,o2,…,oT)
输出: 状态序列 I = ( i 1 , i 2 , … , i T ) I=(i_1,i_2,\dots,i_T) I=(i1,i2,…,iT)因为状态序列是隐藏的,不可观测的,所以叫解码
HMM存在三个基本问题:
-给定模型参数和观测数据,估计隐藏状态的最优序列
-给定模型参数和观测数据,计算数据的可能性
-仅在给定观测数据的情况下,估计模型参数
第一个和第二个问题可以分别通过称为维特比算法和前向-后向算法的动态编程算法来解决。最后一个问题可以通过迭代期望最大化(EM)算法来解决,该算法被称为Baum-Welch算法
算法
观测序列生成算法
输入: λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π) ,观测序列长度 T T T
输出:观测序列 O = ( o 1 , o 2 , … , o T ) O=(o_1,o_2,\dots,o_T) O=(o1,o2,…,oT)
- 按照初始状态分布 π \pi π产生 i 1 i_1 i1
- t = 1 t=1 t=1
- 按照状态 i t i_t it的观测概率分布 b i t ( k ) b_{i_t}(k) bit(k)生成 o t o_t ot
- 按照状态 i t i_t it的状态转移概率分布 { a i t , i t + 1 } \{a_{i_t, {i_{t+1}}}\} {ait,it+1}产生状态 i t + 1 i_{t+1} it+1, i t + 1 = 1 , 2 , … , N \color{red}i_{t+1}=1,2,\dots,N it+1=1,2,…,N
- t = t + 1 t=t+1 t=t+1 如果 t < T t<T t<T转到3,否则,终止
书中定义了
I
=
(
i
1
,
i
2
,
…
,
i
T
)
,
Q
=
{
q
1
,
q
2
,
…
,
q
T
}
I=(i_1,i_2,\dots,i_T), Q=\{q_1,q_2,\dots,q_T\}
I=(i1,i2,…,iT),Q={q1,q2,…,qT}根据定义,
i
t
i_t
it的取值集合应该是
Q
Q
Q,而上面算法描述中说明了
i
t
+
1
=
1
,
2
,
…
,
N
\color{red}i_{t+1}=1,2,\dots,N
it+1=1,2,…,N
注意这里面的
i
t
i_t
it实际上不是状态, 而是对应了前面的
i
,
j
i,j
i,j的含义,实际的状态应该是
q
i
t
q_{i_t}
qit这个算法中的
a
i
t
i
t
+
1
=
P
(
i
t
+
1
=
q
i
t
+
1
∣
i
t
=
q
i
t
)
a_{i_ti_{t+1}}=P(i_{t+1}=q_{i_{t+1}}|i_t=q_{i_t})
aitit+1=P(it+1=qit+1∣it=qit) 这里同样的符号,表示了两个不同的含义
概率计算算法
前向概率与后向概率
给定马尔可夫模型 λ \lambda λ, 定义到时刻 t t t部分观测序列为 o 1 , o 2 , … , o t o_1, o_2, \dots ,o_t o1,o2,…,ot, 且状态 q i q_i qi的概率为前向概率, 记作
α t ( i ) = P ( o 1 , o 2 , … , o t , i t = q i ∣ λ ) \alpha_t(i)=P(o_1,o_2,\dots,o_t,i_t=q_i|\lambda) αt(i)=P(o1,o2,…,ot,it=qi∣λ)
给定马尔可夫模型 λ \lambda λ, 定义到时刻 t t t状态为 q i q_i qi的条件下, 从 t + 1 t+1 t+1到 T T T的部分观测序列为 o t + 1 , o t + 2 , … , o T o_{t+1}, o_{t+2}, \dots ,o_T ot+1,ot+2,…,oT的概率为后向概率, 记作
β t ( i ) = P ( o t + 1 , o t + 2 , … , o T ∣ i t = q i , λ ) \beta_t(i)=P(o_{t+1},o_{t+2},\dots,o_T|i_t=q_i, \lambda) βt(i)=P(ot+1,ot+2,…,oT∣it=qi,λ)
关于 α 和 β 这两个公式 , 仔细看下 , 细心理解 . \color{red} 关于\alpha 和\beta 这两个公式, 仔细看下, 细心理解. 关于α和β这两个公式,仔细看下,细心理解. 前向概率从前往后递推, 后向概率从后向前递推。
前向算法
输入: λ , O \lambda , O λ,O
输出: P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
初值
α 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , … , N \alpha_1(i)=\pi_ib_i(o_1), i=1,2,\dots,N α1(i)=πibi(o1),i=1,2,…,N
观测值 o 1 o_1 o1, i i i的含义是对应状态 q i q_i qi这里 α \alpha α 是 N N N维向量, 和状态集合 Q Q Q的大小 N N N有关系. α \alpha α是个联合概率.
递推
α t + 1 ( i ) = [ ∑ j = 1 N α t ( j ) a j i ] b i ( o t + 1 ) , i = 1 , 2 , … , N , t = 1 , 2 , … , T − 1 \color{red}\alpha_{t+1}(i) = \left[\sum\limits_{j=1}^N\alpha_t(j)a_{ji}\right]b_i(o_{t+1})\color{black}, \ i=1,2,\dots,N, \ t = 1,2,\dots,T-1 αt+1(i)=[j=1∑Nαt(j)aji]bi(ot+1), i=1,2,…,N, t=1,2,…,T−1
转移矩阵 A A A维度 N × N N\times N N×N, 观测矩阵 B B B维度 N × M N\times M N×M, 具体的观测值 o o o可以表示成one-hot形式, 维度 M × 1 M\times1 M×1, 所以 α \alpha α的维度是 α = α A B o = 1 × N × N × N × N × M × M × N = 1 × N \alpha = \alpha ABo=1\times N\times N\times N \times N\times M \times M\times N=1\times N α=αABo=1×N×N×N×N×M×M×N=1×N终止
P ( O ∣ λ ) = ∑ i = 1 N α T ( i ) = ∑ i = 1 N α T ( i ) β T ( i ) P(O|\lambda)=\sum\limits_{i=1}^N\alpha_T(i)=\color{red}\sum\limits_{i=1}^N\alpha_T(i)\beta_T(i) P(O∣λ)=i=1∑NαT(i)=i=1∑NαT(i)βT(i)
注意, 这里 O → ( o 1 , o 2 , o 3 , … , o t ) O\rightarrow (o_1, o_2, o_3,\dots, o_t) O→(o1,o2,o3,…,ot), α i \alpha_i αi见前面前向概率的定义 P ( o 1 , o 2 , … , o t , i t = q i ∣ λ ) P(o_1,o_2,\dots,o_t,i_t=q_i|\lambda) P(o1,o2,…,ot,it=qi∣λ), 所以, 对 i i i求和能把联合概率中的 I I I消掉.这个书里面解释的部分有说.
书中有说前向算法的关键是其局部计算前向概率, 然后利用路径结构将前向概率"递推"到全局.
减少计算量的原因在于每一次计算直接引用前一时刻的计算结果, 避免重复计算.
前向算法计算 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)的复杂度是 O ( N 2 T ) O(N^2T) O(N2T)阶的,直接计算的复杂度是 O ( T N T ) O(TN^T) O(TNT)阶,所以 T = 2 T=2 T=2时候并没什么改善。
红色部分为后补充了 β T ( i ) \beta_T(i) βT(i)项,这项为1,此处注意和后面的后向概率对比。
后向算法
输入: λ , O \lambda , O λ,O
输出: P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
终值
β T ( i ) = 1 , i = 1 , 2 , … , N \beta_T(i)=1, i=1,2,\dots,N βT(i)=1,i=1,2,…,N
在 t = T t=T t=T时刻, 观测序列已经确定.递推
β t ( i ) = ∑ j = 1 N a i j b j ( o t + 1 ) β t + 1 ( j ) , i = 1 , 2 , … , N , t = T − 1 , T − 2 , … , 1 \color{red}\beta_t(i)=\sum\limits_{j=1}^Na_{ij}b_j(o_{t+1})\beta_{t+1}(j)\color{black}, i=1,2,\dots,N, t=T-1, T-2,\dots,1 βt(i)=j=1∑Naijbj(ot+1)βt+1(j),i=1,2,…,N,t=T−1,T−2,…,1
从后往前推
β = A B o β = N × N × N × M × M × N × N × 1 = N × 1 \beta = ABo\beta = N \times N \times N \times M \times M \times N \times N \times 1 = N \times 1 β=ABoβ=N×N×N×M×M×N×N×1=N×1P ( O ∣ λ ) = ∑ i = 1 N π i b i ( o 1 ) β 1 ( i ) = ∑ i = 1 α 1 ( i ) β 1 ( i ) P(O|\lambda)=\sum\limits_{i=1}^N\pi_ib_i(o_1)\beta_1(i)=\color{red}\sum\limits_{i=1}\alpha_1(i)\beta_1(i) P(O∣λ)=i=1∑Nπibi(o1)β1(i)=i=1∑α1(i)β1(i)
- 这里需要注意下,按照后向算法, β \beta β在递推过程中会越来越小,如果层数较多,怕是 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)会消失
- 另外一个要注意的点 o t + 1 β t + 1 \color{red}o_{t+1}\beta_{t+1} ot+1βt+1
- 注意,红色部分为后补充,结合前面的前向概率最后的红色部分一起理解
小结
求解的都是观测序列概率
观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)统一写成
P ( O ∣ λ ) = ∑ i = 1 N ∑ j = 1 N α t ( i ) a i j b j ( o t + 1 β t + 1 ( j ) ) , t = 1 , 2 , … , T − 1 P(O|\lambda)=\sum_{i=1}^N\sum_{j=1}^N\alpha_t(i)a_{ij}b_j(o_{t+1}\beta_{t+1}(j)),\ t=1,2,\dots,T-1 P(O∣λ)=i=1∑Nj=1∑Nαt(i)aijbj(ot+1βt+1(j)), t=1,2,…,T−1P ( O ∣ λ ) = α A B o β P(O|\lambda) = \alpha ABo\beta P(O∣λ)=αABoβ
其实前向和后向不是为了求整个序列
O
O
O的概率,是为了求中间的某个点
t
t
t,前向后向主要是有这个关系:
α
t
(
i
)
β
t
(
i
)
=
P
(
i
t
=
q
i
,
O
∣
λ
)
\alpha_t(i)\beta_t(i)=P(i_t=q_i,O|\lambda)
αt(i)βt(i)=P(it=qi,O∣λ)
当
t
=
1
t=1
t=1或者
t
=
T
−
1
t=T-1
t=T−1的时候,单独用后向和前向就可以求得
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ),分别利用前向和后向算法均可以求解
P
(
O
∣
λ
)
P(O|\lambda)
P(O∣λ),结果一致。
利用上述关系可以得到下面一些概率和期望,这些概率和期望的表达式在后面估计模型参数的时候有应用。
概率与期望
- 输入模型 λ \lambda λ与观测 O O O,输出在时刻 t t t处于状态 q i q_i qi的概率 γ t ( i ) \gamma_t(i) γt(i)
- 输入模型 λ \lambda λ与观测 O O O,输出在时刻 t t t处于状态 q i q_i qi且在时刻 t + 1 t+1 t+1处于状态 q j q_j qj的概率 ξ t ( i , j ) \xi_t(i,j) ξt(i,j)
- 在观测 O O O下状态 i i i出现的期望值
- 在观测 O O O下状态 i i i转移的期望值
- 在观测 O O O下状态 i i i转移到状态 j j j的期望值
学习问题
监督学习方法
效果好,费钱,如果有钱能拿到标注数据,不用犹豫,去干吧。
Baum-Welch算法
马尔可夫模型实际上是一个含有隐变量的概率模型
P
(
O
∣
λ
)
=
∑
I
P
(
O
∣
I
,
λ
)
P
(
I
∣
λ
)
P(O|\lambda)=\sum\limits_IP(O|I,\lambda)P(I|\lambda)
P(O∣λ)=I∑P(O∣I,λ)P(I∣λ)
关于EM算法可以参考第九章, 对隐变量求期望,
Q
Q
Q函数极大化
输入: 观测数据 O = ( o 1 , o 2 , … , o T ) O=(o_1, o_2, \dots, o_T) O=(o1,o2,…,oT)
输出: 隐马尔可夫模型参数
初始化
对 n = 0 n=0 n=0,选取 a i j ( 0 ) , b j ( k ) ( 0 ) , π i ( 0 ) a_{ij}^{(0)}, b_j(k)^{(0)}, \pi_i^{(0)} aij(0),bj(k)(0),πi(0),得到模型参数 λ ( 0 ) = ( A ( 0 ) , B ( 0 ) , π ( 0 ) ) \lambda^{(0)}=(A^{(0)}, B^{(0)},\pi^{(0)}) λ(0)=(A(0),B(0),π(0))递推
对 n = 1 , 2 , … , n=1,2,\dots, n=1,2,…,
a i j ( n + 1 ) = ∑ t = 1 T − 1 ξ t ( i , j ) ∑ t = 1 T − 1 γ t ( i ) a_{ij}^{(n+1)}=\frac{\sum\limits_{t=1}^{T-1}\xi_t(i,j)}{\sum\limits_{t=1}^{T-1}\gamma_t(i)} aij(n+1)=t=1∑T−1γt(i)t=1∑T−1ξt(i,j)b j ( k ) ( n + 1 ) = ∑ t = 1 , o t = v k T γ t ( j ) ∑ t = 1 T γ t ( j ) b_j(k)^{(n+1)}=\frac{\sum\limits_{t=1,o_t=v_k}^{T}\gamma_t(j)}{\sum\limits_{t=1}^T\gamma_t(j)} bj(k)(n+1)=t=1∑Tγt(j)t=1,ot=vk∑Tγt(j)
π i ( n + 1 ) = γ 1 ( i ) \pi_i^{(n+1)}=\gamma_1(i) πi(n+1)=γ1(i)
- 终止
得到模型参数 λ ( n + 1 ) = ( A ( n + 1 ) , B ( n + 1 ) , π ( n + 1 ) ) \lambda^{(n+1)}=(A^{(n+1)}, B^{(n+1)},\pi^{(n+1)}) λ(n+1)=(A(n+1),B(n+1),π(n+1))
理解:
单独说一下这个问题,公式里面求和有个 o t = v k o_t=v_k ot=vk, 什么意思?
γ \gamma γ的维度应该是 N × T N\times T N×T,通过 ∑ t = 1 T \sum\limits_{t=1}^T t=1∑T可以降维到 N N N,但是实际上 B B B的维度是 N × M N\times M N×M,所以有了这个表达,书中对应部分的表达在 P 172 的 10.3 P_{172}的10.3 P172的10.3,也说明了 b j ( k ) b_j(k) bj(k)的具体定义。
注意这里
b
j
(
k
)
b_j(k)
bj(k)并不要求是离散的,可以定义为一个连续的函数, 所以书中这样的表达更通用一些,关于这点在本章大参考文献[^5]中有部分内容讨论,见Special cases of the B parameters。
这里涉及到实际实现的时候,可以考虑把观测序列 O O O转换成one-hot的形式, O o n e _ h o t O_{one\_hot} Oone_hot维度为 M × T M\times T M×T, B B B的维度 N × M N\times M N×M, B ⋅ O B\cdot O B⋅O之后,转换成观测序列对应的发射概率矩阵,维度为 N × T N\times T N×T。
补充一下, o t = v k o_t=v_k ot=vk有另外一种表达是$ \sigma_{o_t,v_k}$, 克罗内克函数。
克罗内克函数是一个二元函数, 自变量一般是两个整数, 如果两者相等, 输出是1, 否则为0.
其实和指示函数差不多, 只不过条件只限制在了相等。
σ
i
j
=
{
1
(
i
=
j
)
0
(
i
≠
j
)
b
j
(
k
)
=
∑
t
=
1
,
o
t
=
v
k
T
γ
t
(
j
)
∑
t
=
1
T
γ
t
(
j
)
=
∑
t
=
1
T
σ
o
t
,
v
k
γ
t
(
j
)
∑
t
=
1
T
γ
t
(
j
)
\sigma_{ij}= \begin{cases} 1 (i = j)\\ 0 (i\ne j) \end{cases} \\ b_j(k)=\frac{\sum\limits_{t=1,o_t=v_k}^{T}\gamma_t(j)}{\sum\limits_{t=1}^T\gamma_t(j)}=\frac{\sum\limits_{t=1}^{T}\sigma_{o_t,v_k}\gamma_t(j)}{\sum\limits_{t=1}^T\gamma_t(j)}
σij={1(i=j)0(i=j)bj(k)=t=1∑Tγt(j)t=1,ot=vk∑Tγt(j)=t=1∑Tγt(j)t=1∑Tσot,vkγt(j)
E E E步与 M M M步的理解
Baum-Welch算法是EM算法在隐马尔可夫模型学习中的具体实现, 由Baum和Welch提出.
看到书上这里都知道是EM算法, 具体实现 哪里是 E , 哪里是 M ? \color{red}哪里是E,哪里是M? 哪里是E,哪里是M?
书中在前向后向算法介绍之后, 单独有一个小节介绍了"一些概率与期望值的计算", 这部分内容在后面的Baum
-Welch算法中会用到, 代码实现的时候才理解, 这小节对应的是E步概率和期望, 后面算法里面的是M步的内容, 说明如何用这些概率和期望去更新HMM模型的参数.
重新梳理一下整个10.2节的内容,这部分内容描述**概率计算方法 **, 实际上在E步操作的时候都要用到,需要用到前向后向算法根据模型参数 A , B , π A,B,\pi A,B,π来更新 α \alpha α和 β \beta β,然后利用这两个值来更新一些概率和期望,再通过模型参数的递推公式来更新模型参数。
这里可能还有点疑问,EM算法的描述里面,E步计算的是Q函数,但是前面的描述似乎并没有显示Q函数和这些工作之间的关系。另外,M步具体操作是参数更新的递推公式,怎么就是最大化了呢? 书中 P 182 P_{182} P182的推导也许能解释这个问题。
看到这里, 感觉书上真的是一句废话都没有…
这部分的理解,要再结合第九章的内容反复一下,应该会有新的体会。
注意E步计算Q函数
Q
(
λ
,
λ
ˉ
)
=
∑
I
log
P
(
O
,
I
∣
λ
)
P
(
O
,
I
∣
λ
ˉ
)
Q(\lambda,\bar{\lambda})=\sum_I\log P(O,I|\lambda)P(O,I|\bar\lambda)
Q(λ,λˉ)=I∑logP(O,I∣λ)P(O,I∣λˉ)
对比一下算法9.1,
P
(
O
,
I
∣
λ
ˉ
)
=
P
(
I
∣
O
,
λ
ˉ
)
P
(
O
∣
λ
ˉ
)
P(O,I|\bar\lambda)=P(I|O,\bar\lambda)P(O|\bar\lambda)
P(O,I∣λˉ)=P(I∣O,λˉ)P(O∣λˉ),所以书中在这个地方有个注释,略去了对于
λ
\lambda
λ而言的常数因子
1
/
P
(
O
∣
λ
ˉ
)
1/P(O|\bar\lambda)
1/P(O∣λˉ)
预测算法
近似算法(MAP)
每个时刻最有可能的状态
i
t
∗
i_t^*
it∗是
i
t
∗
=
arg
max
1
⩽
i
⩽
N
[
γ
t
(
i
)
]
,
t
=
1
,
2
,
…
,
T
i_t^*=\arg \max\limits_{1\leqslant i\leqslant N}\left[\gamma_t(i)\right], t=1,2,\dots,T
it∗=arg1⩽i⩽Nmax[γt(i)],t=1,2,…,T
得到序列
I
∗
=
(
i
1
∗
,
i
2
∗
,
…
,
i
T
∗
)
I^*=(i_1^*,i_2^*,\dots,i_T^*)
I∗=(i1∗,i2∗,…,iT∗)
这个算法, 在输出每个状态的时候, 只考虑了当前的状态.
维特比算法(Viterbi)
输入: 模型 λ = ( A , B , π ) \lambda=(A, B, \pi) λ=(A,B,π)和观测 O = ( o 1 , o 2 , … , o T ) O=(o_1, o_2,\dots,o_T) O=(o1,o2,…,oT)
输出: 最优路径 I ∗ = ( i 1 ∗ , i 2 ∗ , … , i T ∗ ) I^*=(i_1^*, i_2^*,\dots,i_T^*) I∗=(i1∗,i2∗,…,iT∗)
- 初始化
δ 1 ( i ) = π i b i ( o 1 ) , i = 1 , 2 , … , N \delta_1(i)=\pi_ib_i(o_1), i=1,2,\dots,N δ1(i)=πibi(o1),i=1,2,…,N
ψ 1 ( i ) = 0 , i = 1 , 2 , … , N \psi_1(i)=0, i=1,2,\dots,N ψ1(i)=0,i=1,2,…,N- 递推
t = 2 , 3 , … , T t=2,3,\dots,T t=2,3,…,T
δ t ( i ) = max 1 ⩽ j ⩽ N [ δ t − 1 ( j ) a j i ] b i ( o t ) , i = 1 , 2 , … , N \delta_t(i)=\max\limits_{1\leqslant j \leqslant N}\left[\delta_{t-1}(j)a_{ji}\right]b_i(o_t), i=1,2,\dots,N δt(i)=1⩽j⩽Nmax[δt−1(j)aji]bi(ot),i=1,2,…,N
ψ t ( j ) = arg max 1 ⩽ j ⩽ N [ δ t − 1 ( j ) a j i ] , i = 1 , 2 , … , N \psi_t(j)=\arg\max\limits_{1\leqslant j \leqslant N}\left[\delta_{t-1}(j)a_{ji}\right], i=1,2,\dots,N ψt(j)=arg1⩽j⩽Nmax[δt−1(j)aji],i=1,2,…,N- 终止
P ∗ = max 1 ⩽ i ⩽ N δ T ( i ) P^*=\max\limits_{1\leqslant i\leqslant N}\delta_T(i) P∗=1⩽i⩽NmaxδT(i)
i T ∗ = arg max 1 ⩽ i ⩽ N [ δ T ( i ) ] i_T^*=\arg\max\limits_{1\leqslant i \leqslant N}\left[ \delta_T(i)\right] iT∗=arg1⩽i⩽Nmax[δT(i)]- 最优路径回溯
t = T − 1 , T − 2 , … , 1 t=T-1, T-2, \dots,1 t=T−1,T−2,…,1
i t ∗ = ψ t + 1 ( i i + 1 ∗ ) i_t^*=\psi_{t+1}(i_{i+1}^*) it∗=ψt+1(ii+1∗)
书上配了个图,这个图可视化了 δ \delta δ