设计切换函数/滑模面S（x）
线性：
滑模面参数确定方法：Hurwitz
保证多项式
为Hurwitz，即特征值在左半平面。
主要适用于速度和精度要求都不高的非线性系统
非线性 《滑模变结构控制理论研究综述》
终端滑模控制：在有限时间内到达平衡点，引入非线性部分
，改善收敛速度
积分滑模控制：增加状态变量的积分项，可以削弱抖振、减小误差，但当初始状态过大会引起超调或饱和
分段线性滑模控制：分成多段线性滑模面
时变滑模面：时变滑模面可随系统的状态或时间改变而改变，使系统始终运行在滑模状态
求控制律u
设计趋近律，将其与
方程联立求得控制律
利用Lyapunov判据，利用
,反推出满足条件的控制律
在实际控制器设计总，为了保证稳定性不能做到每次输出都要进行Lyapunov判据，因此常采用趋近律方式。
常见趋近律
等速趋近律：
指数趋近律：
幂次趋近律：
一般趋近律：
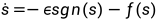
Lyapunov函数设计
构造Lyapunov函数没有通用方法，每种方法都有自己的局限性，具有技巧性。
线性滑模面常用的Lyapunov函数为
，其导数为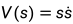
滑模控制的设计步骤
根据系统得出状态方程
设计滑模面
设计趋近律求出控制器表达
利用Lyapunov函数证明稳定性，保证s=0可达
若使用反推法求控制律，则先设计Lyapunov函数，求导后设计控制律以满足稳定性条件。
抖振
当系统到达滑模面时速度并不为0，因此会穿过滑模面造成抖振。
根本原因是开关的切换动作造成的控制不连续性。
改变切换函数（此处不是滑模面的意思）减小抖振：
符号函数：sgn（s）
饱和函数
双曲正切函数：
改变趋近律
滤波方法：消除高频抖振
观测器方法：用观测器观测外界干扰和不确定项，根据观测值设计切换增益
智能控制方法：模糊控制、神经网络控制、优化方法
滑模控制器与滑模观测器的区别
滑模观测器是一类动态系统，根据系统的外部变量（输入与输出）的实测值得出状态变量估计值的一类动态系统。与滑模控制的原理相似，用处不同。
滑模观测器设计步骤：
建立系统的状态方程
在方程基础上增加滑模控制量
利用MATLAB测试出合适的参数值
等效滑模控制
利用反推求控制律与等效滑模控制思维相似，在等效滑模控制中：
。首先通过
求得等效控制
，再通过
，该式中控制律为整体u，进而获得切换鲁棒项
自适应滑模控制分析流程
以上是学习滑模控制的部分内容总结，如有错误欢迎指正。
参考网站
【控制理论】滑模控制最强解析 - 北极星！- 博客园 (cnblogs.com)
【控制】滑模控制，滑模面的选择_滑模面如何设计_Zhao-Jichao的博客-CSDN博客
【控制理论】滑模控制最强解析_Y-box的博客-CSDN博客_滑模控制
滑模控制的一种简单理解 - 知乎 (zhihu.com)
非线性系统总结——非线性设计工具 - 知乎 (zhihu.com)
滑模控制器、滑模观测器解释 - 知乎(zhihu.com)
https://blog.csdn.net/yuanxun9785/article/details/121246612
