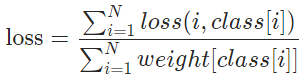- 近独立粒子:粒子之间相互作用微弱
- 基本粒子中,自旋量子数为半整数的有
- 电子 、 质子 、中子、中微子
- 自旋量子数为整数的有
- 光子、pi介子
- 经典力学描述系统的微观运动状态
- 经典力学中,全同粒子可以分辨
- 量子力学,全同粒子不可以分辨
- 微观粒子的全同性原理
- 全同粒子是不可分辨的,将任何两个全同粒子对换,不改变整个系统的微观运动状态。
- 玻色子和费米子
- 费米子: 自旋量子数为半整数
- 玻色子: 自旋量子数为整数
- 量子系统
- 费米系统:由费米子组成的系统
- 遵从泡利不相容原理,一个个体量子态最多能容纳 一个费米子
- 玻色系统:由玻色子组成的系统
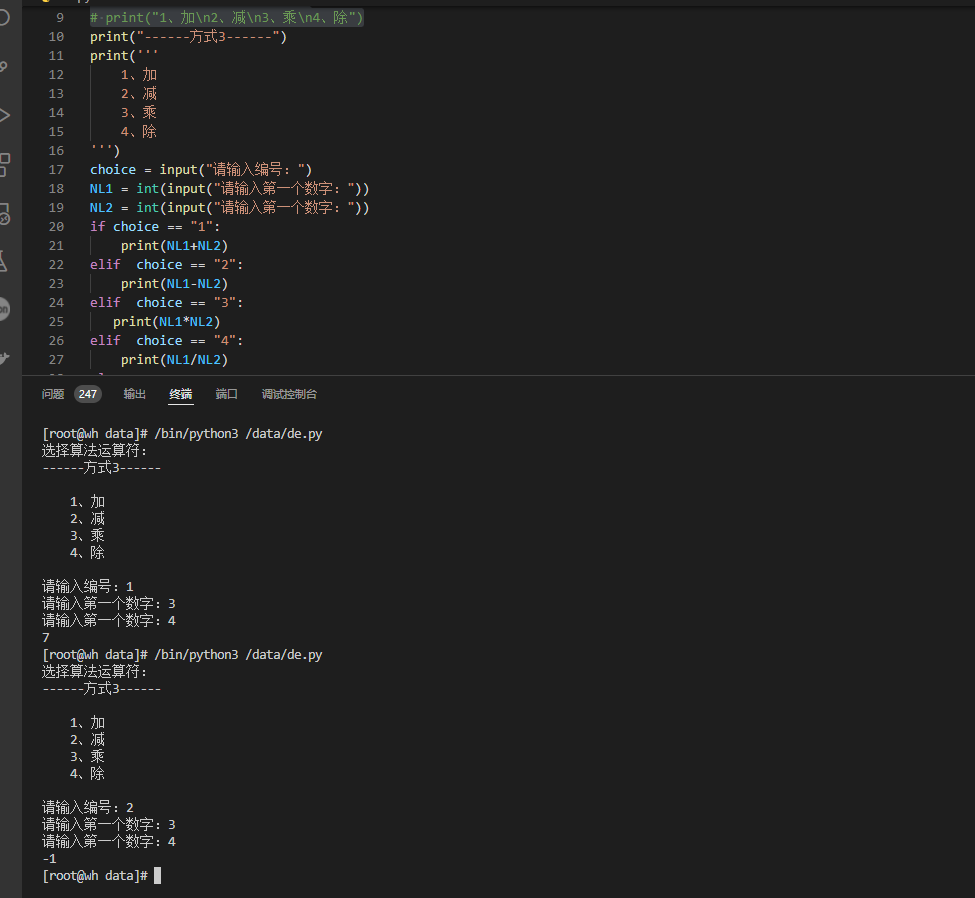
- 处在同一个个体量子态的玻色子的数目不受限制
- 玻耳兹曼系统:
- 可分辨的全同近独立粒子组成,处在一个个体量子态上的粒子数不受限制
- 费米系统:由费米子组成的系统
- 玻耳兹曼等概率原理
- 对于处在平衡状态的孤立系统,系统各个可能的微观状态出现的概率是相等的
系统
玻耳兹曼系统
- 粒子可以分辨,一个量子态可容纳的粒子数不受限制
- step1:对于能级
,
个粒子分别占据
个量子态
- step2:不同能级的粒子交换位置
- 那么,玻尔兹曼分布对应的微观状态数:
玻色系统
- 粒子不可分辨,每个量子态能容纳的粒子数不受限制
- 粒子之间的相互交换共有方式:
- 全同粒子的交换不形成新的量子态
- 量子态之间的相互交换共有方式:
- 包含在粒子与量子态的交换中
- 对于能级
,
个粒子占据量子态共有方式:
- 玻色系统相应的微观状态数为:
费米系统
- 粒子不可分辨,每一个个体量子态最多只能容纳一个粒子
- 对能级
,
个粒子占据量子态共有方式
- 费米系统对应的微观状态数:
分布
玻耳兹曼分布
,