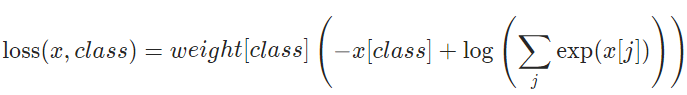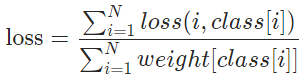李宏毅机器学习2023作业04Self-attention、李宏毅机器学习2023作业03CNN和李宏毅机器学习2023作业02Classification都是分类问题，都涉及到了交叉熵损失函数以及起正则作用的标签平滑技巧，本次博文把以上两点整理总结下。

基本概念

1、信息量：在信息论中，一个不太可能发生的事件居然发生了，我们收到的信息要多于一个非常可能发生的事情发生。因此，事件包含的信息量应与其发生的概率负相关。数学表达式定义为：假设$X$是取值集合为 { x 1 , x 2 , . . . , x n } \{x_1,x_2,...,x_n\} {x1​,x2​,...,xn​} 的离散型随机变量，定义事件$X=x_i$的信息量为$I(x_i)=-{\log }_{2}P(X=x_i)$。
  这里采用$\log$函数的形式主要是为了体现信息量的三个性质：事件发生的概率越低，信息量越大；事件发生的概率越高，信息量越低；多个事件同时发生的概率是多个事件概率相乘，总信息量是多个事件信息量相加。

2、熵：通常用熵对整个事件的平均信息量进行描述，即上述信息量定义关于概率分布$P$的期望：
$$\mathrm{H}(P)={\mathbb{E}}_{X\sim P}[-{\log }_{2}P(x)]=-\sum _{i=1}^{n}P(x_i)\cdot {\log }_{2}P(x_i)$$总而言之，信息熵是用来衡量事物不确定性的，信息熵越大，事物越具不确定性。通常接近确定性的分布（输出几乎可以确定）具有较低的熵，那些接近均匀分布的概率分布具有较高的熵。

3、KL散度（相对熵）：一般被用于计算两个分布之间的不同：
$${\mathrm{D}}_{KL}(P||Q)={\mathbb{E}}_{X\sim P}[{\log }_2\frac{P(x)}{Q(x)}]=\sum _{i=1}^{n}P(x_i)\cdot {\log }_2\frac{P(x_i)}{Q(x_i)}$$将上式展开之后可以发现前者是熵，而后者通常定义为交叉熵，因此KL散度（相对熵）=交叉熵-熵

4、交叉熵：
$$\mathrm{H}(P,Q)={\mathbb{E}}_{X\sim P}[-{\log }_{2}Q(x)]=-\sum _{i=1}^{n}P(x_i)\cdot {\log }_{2}Q(x_i)$$

交叉熵损失函数

1、在深度学习中，我们总是希望模型学到的分布$P(model)$和真实数据的分布$P(real)$越接近越好，最直接的损失函数就是利用KL散度使得两个分布的差异性最小。但我们没有真实数据的分布，那么只能退而求其次，希望模型学到的分布和训练数据的分布$P(training)$尽量相同
2、由于训练数据是给定的，因此KL散度中的熵就是恒定的，那么，最小化交叉熵就是最小化KL散度
3、在分类任务中，训练数据的标签通常才有用one-hot编码的形式，假设类别总数为3类，给定一个样本的标签为$[1,0,0]$的形式，该样本对应的模型输出为$[0.8,0.1,0.1]$的形式，直接代入交叉熵的公式$-(1\cdot {\log }_2(0.8)+0\cdot {\log }_2(0.1)+0\cdot {\log }_2(0.1))=-{\log }_2(0.8)$，计算结果中只有one-hot编码形式的标签中为1的对应项。在具体的Pytorch代码中，几行代码就可以实现交叉熵损失函数的定义、计算损失、计算梯度:

criterion = nn.CrossEntropyLoss()
......
output_tensor = model(input_tensor)
loss = criterion(output_tensor, target_tensor)
loss.backward()
...... 

Pytorch代码实现

1、在Pytorch1.9.0中，交叉熵损失函数的定义形式如下：

紧接着“This criterion combines LogSoftmax and NLLLoss in one single class.”的描述给出了两点信息：一是包含了LogSoftmax和NLLLoss两个函数，二是用于单类别问题（即一个样本只对应一个类别）
2、函数中第一个参数$weight$是可手动定义的1D Tensor，假如分类问题类别总数为$C$，参数$weight$的长度就是$C$，在训练集中各个类别占比不平衡时通过设置不同的权重会特别有用；第二个参数$size\_average$和第四个参数$reduce$已经被替代为第五个参数$reduction$，默认为${}^{\prime }mea{n}^{\prime }$，对一个$batch$范围内所有样本的交叉熵损失求平均，也可以取值${}^{\prime }su{m}^{\prime }$对一个$batch$范围内所有样本的交叉熵损失求总和以及取值${}^{\prime }non{e}^{\prime }$保持交叉熵损失的尺寸，即与$Target$的尺寸一致；$ignore\_index$表示该类别对应的样本对最终的交叉熵损失没有任何贡献。
3、函数包括2个输入：$Input$、$Target$和1个输出：$Output$，对于$Input$而言，它是来自深度学习模型未归一化的原始的各个类别的置信度，通常对应的尺寸是$batch\times C$或者$batch\times C\times d_1\times d_2\times ...\times d_K$，在2023作业02Classification、2023作业03CNN和2023作业04Self-attention中对应的是$batch\times C$，其中2023作业02Classification的BossBaseline方法是$batch\times C\times SeqLength$，当然如果不嫌麻烦的话，可以把$batch\times C\times d_1\times d_2\times ...\times d_K$通过维度转化，把后面的数据尺寸维度合并到$batch$维转换成二维的形式
4、对于$Target$而言，通常对应的尺寸是$batch$或者$batch\times d_1\times d_2\times ...\times d_K$，取值为$[0,C-1]$，最终交叉熵损失函数就是像上文提到的例子一样，当给定$batch$中的一个样本时，计算结果中只有one-hot编码形式的标签中为1的对应项，下式中$j$是类别索引，取值范围为$[0,C-1]$：

如果考虑参数$weight$，那么会在上式中乘以对应标签类别的权重

通常在一个$batch$范围内对所有样本取平均，就是如下的形式：

可以看出，分母是一个$batch$范围内所有样本对应的真实标签类别的权重之和，意味着对每个样本的交叉熵损失进行了加权平均。
5、自Pytorch1.10开始，torch.nn.CrossEntropyLoss内置了标签平滑的参数$label\_smoothing$，带标签平滑的交叉熵损失函数有点没整明白（网上资料挺多的，但是有点杂），先做个标记吧！ 如下的代码是可以直接用的，和官方的Pytorch代码结果是一致的：

import torch
import torch.nn as nn
import torch.nn.functional as F


def linear_combination(x, y, epsilon):
    return epsilon * x + (1 - epsilon) * y


def reduce_loss(loss, reduction='mean'):
    return loss.mean() if reduction == 'mean' else loss.sum() if reduction == 'sum' else loss


class LabelSmoothingCrossEntropy(nn.Module):
    def __init__(self, epsilon: float = 0.1, reduction='mean'):
        super().__init__()
        self.epsilon = epsilon
        self.reduction = reduction

    def forward(self, preds, target):
        # 如果数据样本除了batch,class_num外还有其他维度，需要先转换成batch*class_num的二维形式
        # 这样就和官方版本的代码完全一致了
        if len(preds.size()) >= 3:
            batch, class_num = preds.size()[0: 2]
            preds = preds.transpose(0, 1).reshape(class_num, -1).transpose(0, 1)
            target = target.reshape(-1)
        n = preds.size()[-1]
        log_preds = F.log_softmax(preds, dim=-1)
        loss = reduce_loss(-log_preds.sum(dim=-1), self.reduction)
        nll = F.nll_loss(log_preds, target, reduction=self.reduction)
        return linear_combination(loss / n, nll, self.epsilon)


criterion1 = LabelSmoothingCrossEntropy()
output = torch.randn(3, 5, 10, requires_grad=True)
target = torch.empty(3, 10, dtype=torch.long).random_(5)
loss1 = criterion1(output, target)
criterion2 = nn.CrossEntropyLoss(label_smoothing=0.1)
loss2 = criterion2(output, target)
print(loss1)
print(loss2)

参考文献

1.PyTorch中的Loss Fucntion
2.百度百科
3.交叉熵损失函数（Cross Entropy Loss）
4.为什么交叉熵（cross-entropy）可以用于计算代价？