概述

GTSAM（Georgia Tech Smoothing and Mapping）是基于因子图的C++库，本篇基于GTSAM对因子图优化做一个简单了解和梳理，并以LIO-SAM为例进一步分析因子图优化在SLAM中的应用。

参考链接：
[0]gtsam官方文档
[1]https://blog.csdn.net/QLeelq/article/details/111368277
[2]https://zhuanlan.zhihu.com/p/621999120

1.基本概念

• 因子图：因子图是一种无向图，由变量和因子组成
• 变量：待优化的状态，可以有多个变量，如机器人位姿、IMU偏置等，每个变量包含了多帧的信息，如位姿X={x1, x2, ... , xn}
• 因子：对应图优化中的边, 即两个变量或者观测与变量之间的约束，如两帧之间的位姿变换、3D点到相机图像的投影关系
• 先验因子：基于GPS或者其他模块得到的观测信息或者位姿初值
• 值：指变量的具体数值

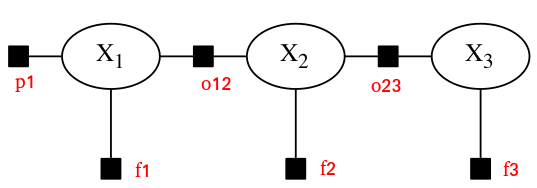
如下图所示，{x1,x2,x3}为变量
黑色方块为因子，其中连接两个变量的为二元因子，如o12, o23;
连接一个变量的为一元因子，如f1, f2, f3, p1,其中p1为先验因子，f1, f2, f3为观测因子

2.官方例子说明

2.1 机器人运动模型

下图为gtsam官方文档中最简单的一个例子，一个基于马尔可夫链的机器人运动模型，即当前时刻的机器人位姿只由机器人上一时刻位姿决定。

如上图所示：

• x1,x2,x3为变量，表示机器人的位姿
• f0为一元先验因子，可以是初始位姿
• f1,f2为二元因子，表示机器人之间的运动，可以是IMU或激光SLAM的里程计信息

2.1.1建立因子图

对于某个问题，在建立关于该问题的数学模型后，就可以基于数学模型建立因子图。gtsam为不同的数学模型内置了现成的模板，在创建因子图时只需要根据不同的模型选择不同的模板即可。
上述机器人运动模型因子图创建过程如下所示：

// step1:构建一个空的非线性因子图
NonlinearFactorGraph graph;

// step2:为因子图添加因子并连接到变量
// [1]构建先验因子，也就是图中的f_0, 这里使用二维姿态（x,y,theta）简化问题
Pose2 priorMean(0.0, 0.0, 0.0);
// [2]初始化高斯噪声，代表我们对该因子的不确定性
noiseModel::Diagonal::shared_ptr priorNoise = noiseModel::Diagonal::Sigmas(Vector3(0.3, 0.3, 0.1));
// [3]将先验因子加入因子图, 其中的1表示该因子连接到第1个变量
graph.add(PriorFactor<Pose2>(1, priorMean, priorNoise));

// [1]构建里程计因子，也就是图中的f_1,f_2, 往前移动2米，y轴不便，theta不变
Pose2 odometry(2.0, 0.0, 0.0);
// [2]初始化高斯噪声
noiseModel::Diagonal::shared_ptr odometryNoise = noiseModel::Diagonal::Sigmas(Vector3(0.2, 0.2, 0.1));
// [3]将里程计因子加入因子图, (1,2)(2,3)分别代表该里程计约束是从变量1到变量2，从变量2到变量3
graph.add(BetweenFactor<Pose2>(1, 2, odometry, odometryNoise));
graph.add(BetweenFactor<Pose2>(2, 3, odometry, odometryNoise));


// step3:设置各个变量的初始值
Values initial;
initial.insert(1, Pose2(0.5, 0.0, 0.2));
initial.insert(2, Pose2(2.3, 0.1, -0.2));
initial.insert(3, Pose2(4.1, 0.1, 0.1));

// step4:调用优化器并使用设定好的初始值对因子图优化
Values result = LevenberMarquardtOptimizer(graph, initial).optimize();

2.3机器人运动建模

进一步的，为上述运动模型添加观测模型，这里以GPS的测量为例

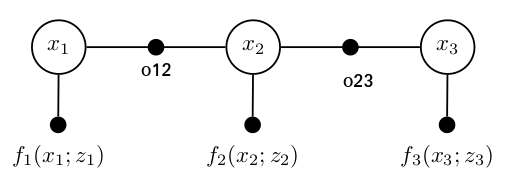
如上图所示：

• x1,x2,x3为变量，表示机器人的位姿
• o12,o23为二元因子，表示机器人之间的运动
• f1,f2,f3为一元观测因子，即GPS的观测值

2.3.1自定义观测因子

通过NoiseModelFactor1<T>模板类定义新的一元因子，其中T为一元因子所对应变量的类型。

需要针对新因子定义一下几个信息：
（1）有关传感器观测值的私有成员变量。
（2）有关因子初始化的构造函数。
（3）用于计算评估误差的误差函数，功能包括：返回变量和观测值之间的残差信息、计算用于非线性优化的雅克比矩阵。

以定义一元GPS因子为例
（1）定义GPS的测量值mx_, my_、
（2）定义GPS因子的构造函数，在使用时通过该函数实例化因子。用给定的x，y值初始化mx_, my_观测值，并给定与该因子连接的变量代号j以及观测的噪声协方差矩阵model。
（3）重载用于计算评估误差的函数evaluateError：残差 = 变量值 - 观测值
公式定义如下：

自定义因子代码如下：

// 自定义因子是Pose2类型的，Pose2对应2D位姿的李群变换矩阵，即3x3的一个矩阵，包括2x2的旋转和2x1的平移
class UnaryFactor: public NoiseModelFactor1<Pose2> {
    // 观测的状态包括x和y两个值 
    double mx_, my_;

public:
    // 成员函数， 在参数列表中初始化所关联变量的Id, 噪声模型， 测量值x和y
    UnaryFactor(Key j, double x, double y, const SharedNoiseModel& model):
        NoiseModelFactor1<Pose2>(model, j), mx_(x), my_(y){}
    // 残差函数模型，残差 = 变量值 - 观测值
    // 输入：当前时刻的位姿q，对误差求导的雅格比矩阵H
    // 位姿q=[qx,qy,angle]为三维，误差为两维，因此误差函数对位姿求导的雅格比矩阵为2x3
    Vector evaluateError(const Pose2& q, boost::optional<Matrix&> H = boost::none) const
    {
        // 如果存在雅格比矩阵，对其进行更新
        if(H)
        {   
            // Jac是误差函数对位姿求导的雅格比矩阵，因为观测函数设置的比较简单，因此雅格比矩阵也很简单，具体的公式推导见下图
            gtsam::Matrix Jac = (Matrix(2,3)<< 1.0,0.0,0.0, 0.0,1.0,0.0).finished();;

            (*H) = Jac;
        }
        return (Vector(2) << q.x() - mx_, q.y() - my_).finished();
    }
};

创建因子图

// step1:构建一个空的非线性因子图
NonlinearFactorGraph graph;
// step2:为因子图添加因子并连接到变量
// 建立观测的噪声模型
noiseModel::Diagonal::shared_ptr unaryNoise = noiseModel::Diagonal::Sigmas(Vector2(0.1, 0.1));
// 加入自定义因子
graph.add(boost::make_shared<UnaryFactor>(1, 0.0, 0.0, unaryNoise));
graph.add(boost::make_shared<UnaryFactor>(2, 2.0, 0.0, unaryNoise));
graph.add(boost::make_shared<UnaryFactor>(3, 4.0, 0.0, unaryNoise));

// step3:设置各个变量的初始值
Values initial;
initial.insert(1, 0.1, 0.0);
initial.insert(2, 2.0, -0.1);
initial.insert(3, 4.1, 0.1);

// step4:调用优化器并使用设定好的初始值对因子图优化
Values result = LevenberMarquardtOptimizer(graph, initial).optimize();

3.LIO-SAM中的因子图应用

3.1IMU因子

在LIO-SAM的imageProjection模块主要对IMU数据进行积分，使用gtsam的IMU预积分模块。该模块订阅雷达里程计的位姿，将该位姿作为初始积分的先验，然后通过gtsam的IMU预积分模块得到IMU高频里程计，同时更新偏置信息，因子图如下：

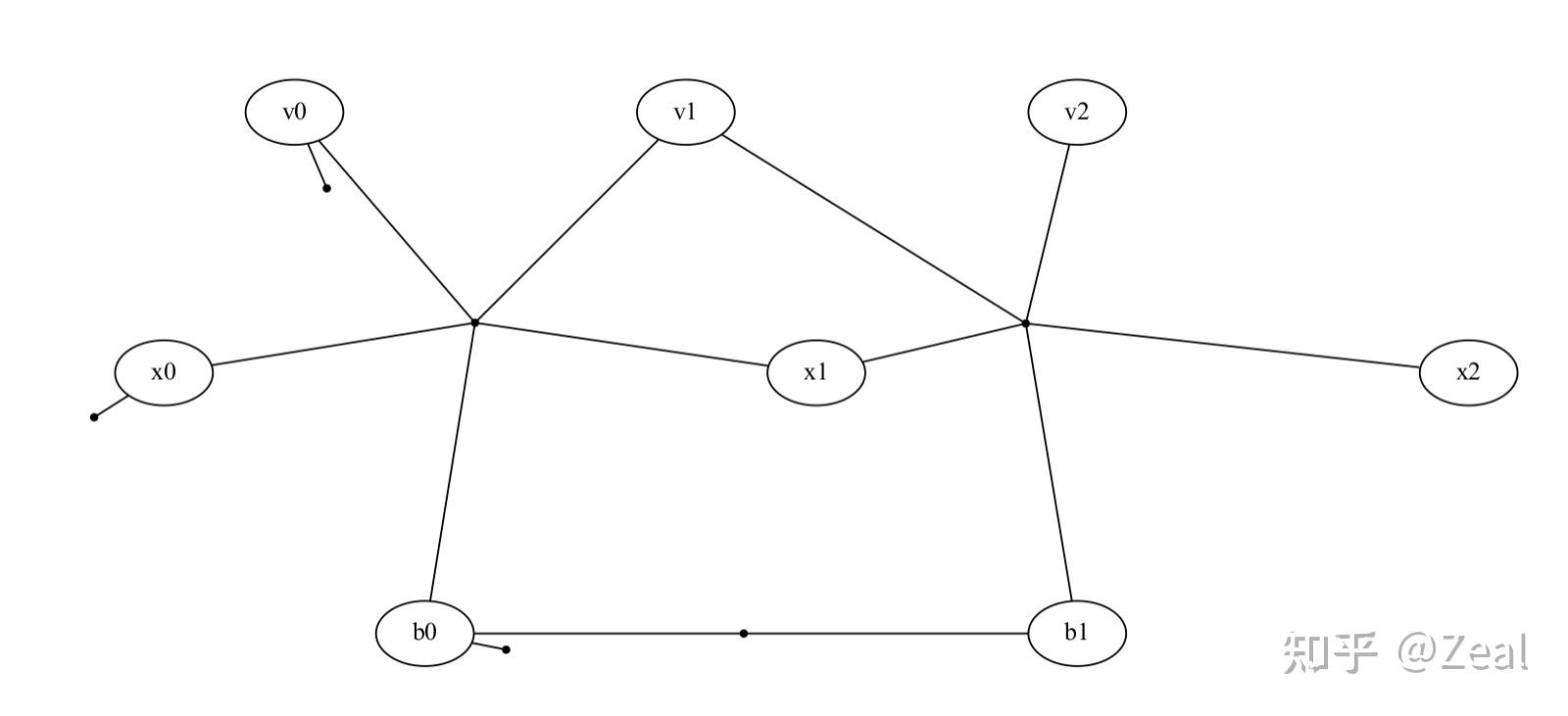
在这个过程中：

• 变量：位姿(旋转和平移)、速度、偏置
• 先验因子：位姿的先验因子为雷达里程计的位姿，速度和偏置的先验因子为0
• 观测因子：IMU因子，每个时刻IMU的角速度加速度，通过观测方程转化为观测值即位姿

1.创建因子图并添加先验因子

// 声明非线性因子图
gtsam::NonlinearFactorGraph graphFactors;

// [1]加入雷达里程计先验因子
// 将雷达里程计位姿转换到IMU坐标系作为先验
prevPose_ = lidarPose.compose(lidar2Imu);
// 创建因子，X(0)表示先验因子连接到X第一个变量，prevPose_为先验因子具体的值，priorPoseNoise为之前定义的噪声
gtsam::PriorFactor<gtsam::Pose3> priorPose(X(0), prevPose_, priorPoseNoise);
// 添加因子
graphFactors.add(priorPose);

// [2]加入速度先验因子
prevVel_ = gtsam::Vector3(0, 0, 0);// 初始化为0
gtsam::PriorFactor<gtsam::Vector3> priorVel(V(0), prevVel_, priorVelNoise);// 创建
graphFactors.add(priorVel);// 加入

// [3]加入Bias先验因子
prevBias_ = gtsam::imuBias::ConstantBias();// 初始化为0
gtsam::PriorFactor<gtsam::imuBias::ConstantBias> priorBias(B(0), prevBias_, priorBiasNoise);// 创建
graphFactors.add(priorBias);// 添加

// 将初始状态设置为因子图变量的初始值
graphValues.insert(X(0), prevPose_);
graphValues.insert(V(0), prevVel_);
graphValues.insert(B(0), prevBias_);

// 使用优化器对变量进行更新
optimizer.update(graphFactors, graphValues);

2.添加IMU因子
通过gtsam自带的积分器，已经将一段时间内(两帧激光之间)的IMU进行了连续积分，积分角速度得到旋转，积分加速度得到线速度和位姿

// 使用IMU预积分的结果构建IMU因子，并加入因子图中
// 将IMU的连续积分结果封装为gtsam::PreintegratedImuMeasurements格式
const gtsam::PreintegratedImuMeasurements& preint_imu = dynamic_cast<const gtsam::PreintegratedImuMeasurements&>(*imuIntegratorOpt_);
// 从preint_imu中拿出一次积分结果即IMU因子，如上图这个因子连接了相邻两个时刻的位姿、速度和上一时刻的Bias
gtsam::ImuFactor imu_factor(X(key - 1), V(key - 1), X(key), V(key), B(key - 1), preint_imu);
graphFactors.add(imu_factor);

// imuIntegratorOpt_->predict输入之前时刻的状态和偏差，预测当前时刻的状态
gtsam::NavState propState_ = imuIntegratorOpt_->predict(prevState_, prevBias_);
// 将IMU预积分的结果作为当前时刻因子图变量的初值
graphValues.insert(X(key), propState_.pose());
graphValues.insert(V(key), propState_.v());
graphValues.insert(B(key), prevBias_);

// 更新一次优化器
optimizer.update(graphFactors, graphValues);
optimizer.update();

// 从优化器中获取当前经过优化后估计值
gtsam::Values result = optimizer.calculateEstimate();
prevPose_  = result.at<gtsam::Pose3>(X(key));
prevVel_   = result.at<gtsam::Vector3>(V(key));
prevState_ = gtsam::NavState(prevPose_, prevVel_);
prevBias_  = result.at<gtsam::imuBias::ConstantBias>(B(key));

2.地图优化

在LIO-SAM的地图优化模块，只在添加关键帧时进行了因子图优化。因子图如下所示：

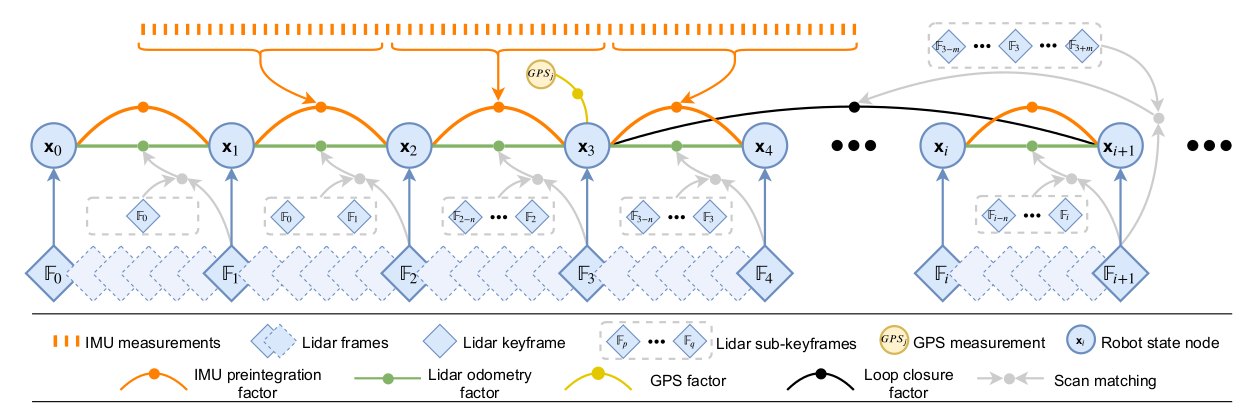
• 变量：关键帧位姿
• 因子：激光里程计因子、GPS因子、回环检测因子

下面一段代码是关于添加激光里程计因子的过程，对于第一帧添加的是PriorFactor类型的先验因子，对于后续帧添加的是BetweenFactor类型的二元因子，过程和上述一样。

void addOdomFactor()
{
    if (cloudKeyPoses3D->points.empty())
    {
        noiseModel::Diagonal::shared_ptr priorNoise = noiseModel::Diagonal::Variances((Vector(6) << 1e-2, 1e-2, M_PI*M_PI, 1e8, 1e8, 1e8).finished()); // rad*rad, meter*meter
        gtSAMgraph.add(PriorFactor<Pose3>(0, trans2gtsamPose(transformTobeMapped), priorNoise));
        initialEstimate.insert(0, trans2gtsamPose(transformTobeMapped));
    }else{
        noiseModel::Diagonal::shared_ptr odometryNoise = noiseModel::Diagonal::Variances((Vector(6) << 1e-6, 1e-6, 1e-6, 1e-4, 1e-4, 1e-4).finished());
        gtsam::Pose3 poseFrom = pclPointTogtsamPose3(cloudKeyPoses6D->points.back());
        gtsam::Pose3 poseTo   = trans2gtsamPose(transformTobeMapped);
        gtSAMgraph.add(BetweenFactor<Pose3>(cloudKeyPoses3D->size()-1, cloudKeyPoses3D->size(), poseFrom.between(poseTo), odometryNoise));
        initialEstimate.insert(cloudKeyPoses3D->size(), poseTo);
    }
}

总结

综上来看，基于gtsam的因子图优化代码结构是比较清晰的，只不过在使用之前需要根据自己的误差模型选择合适的模板，针对里程计类型、GPS类型等gtsam都提供了相应的模板，对于gtsam库中没有的模板可以自行定义。