题目所属分类

二叉树的最大值 dfs

原题链接

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

代码案例：
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

题解

(递归，树的遍历) O(n2)
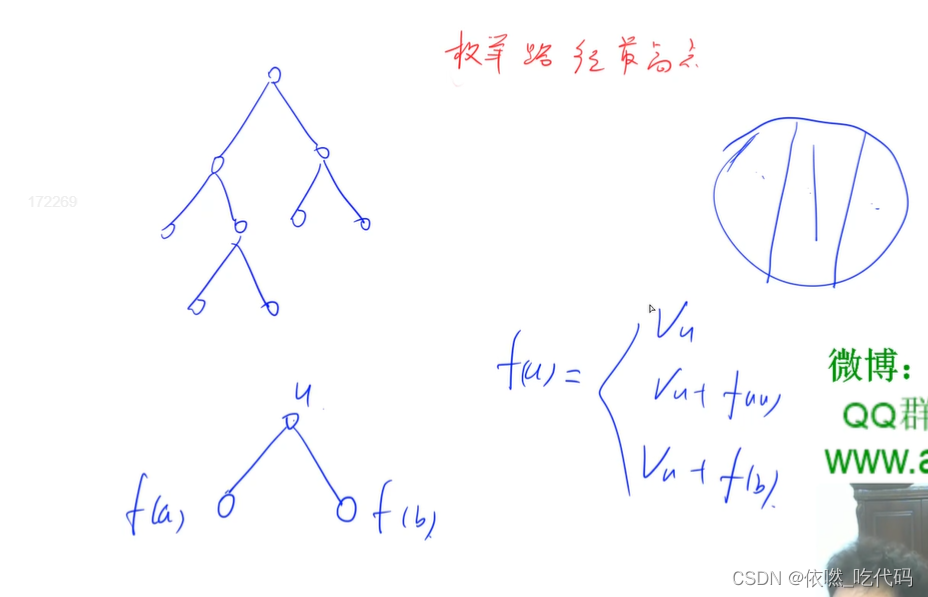
树中每条路径，都存在一个离根节点最近的点，我们把它记为割点，用割点可以将整条路径分为两部分：从该节点向左子树延伸的路径，和从该节点向右子树延伸的部分，而且两部分都是自上而下延伸的。
其实就是LCA 最近公共祖先

我们可以递归遍历整棵树，递归时维护从每个节点开始往下延伸的最大路径和。
对于每个点，递归计算完左右子树后，我们将左右子树维护的两条最大路径，和该点拼接起来，就可以得到以这个点为割点的最大路径。
然后维护从这个点往下延伸的最大路径：从左右子树的路径中选择权值大的一条延伸即可。
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int ans  ;
    public int maxPathSum(TreeNode root) {
        ans = Integer.MIN_VALUE;
        dfs(root);
        return ans ;
    }
    public int dfs(TreeNode root ){
        if(root == null) return 0 ;
        int left = Math.max(0 , dfs(root.left));
        int right = Math.max(0 , dfs(root.right));
        ans = Math.max(ans , left + right + root.val);
        return root.val + Math.max(right , left);
    }
}