目录

字母异位词分组

最大子数组和 

跳跃游戏

合并区间

不同路径 

最小路径和 

爬楼梯 

颜色分类

子集

单词搜索

二叉树的中序遍历 

不同的二叉搜索树 

---

字母异位词分组

题目链接：49. 字母异位词分组

 示例

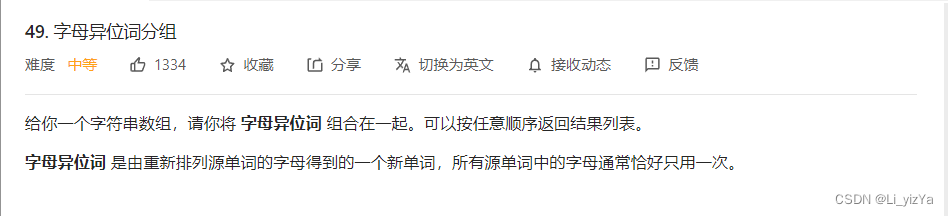
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

解题思路：计数法，遍历每一个字符串，记录其每一个字符出现次数，再按顺序将每个出现次数大于 0 的字母和出现次数拼接成字符串，作为哈希表的键，原字符串作为哈希表的值，将键相同的存入一个链表中，最终将哈希表的值转化为顺序表即可。

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> ret = new HashMap<>();
        for (String str : strs) {
            int[] count = new int[26];
            int length = str.length();
            for (int i = 0; i < length; i++) {
                count[str.charAt(i) - 'a']++;
            }
            //按顺序将字符串拼接
            StringBuffer sb = new StringBuffer();
            for (int i = 0; i < 26; i++) {
                if (count[i] != 0) {
                    sb.append((char) 'a' + i);
                    sb.append(count[i]);
                }
            }
            String key = sb.toString();
            List<String> list = ret.getOrDefault(key, new ArrayList<String>());
            list.add(str);
            ret.put(key, list);
        }
        return new ArrayList<List<String>>(ret.values());
    }
}

最大子数组和 

题目链接：53. 最大子数组和

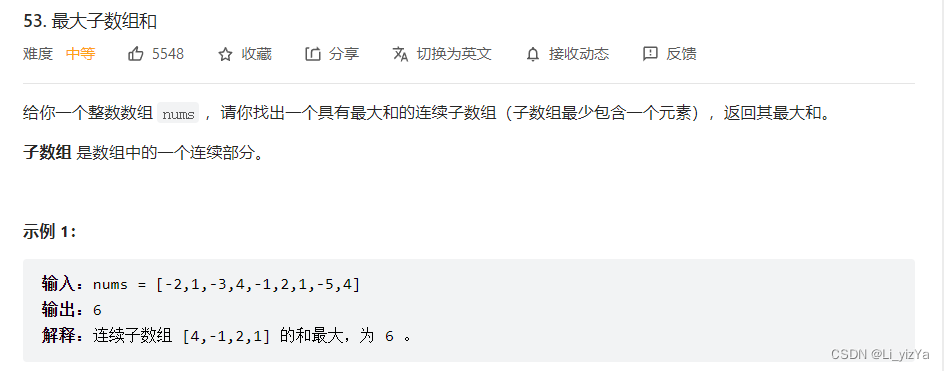
解题思路：动态规划，列出状态、状态方程、初始值

    状态定义：f(i): 下标为i之前连续子数组的最大和
    状态方程：dp[i]=max{nums[i],dp[i−1]+nums[i]}
    初始值：dp[0] = nums[0]
    返回结果：ret 

class Solution {
    /**
    状态定义：dp(i): 以 nums[i] 结尾的连续子数组的最大和
    状态方程：dp[i]=max{nums[i],dp[i−1]+nums[i]}
    初始值：dp[0] = nums[0]
    返回结果：ret
     */
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int[] dp = new int[len];
        dp[0] = nums[0];
        int ret = nums[0];
        for (int i = 1; i < len; i++) {
            dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
            ret = Math.max(dp[i], ret);
        }
        return ret;
    }
}

跳跃游戏

题目链接：55. 跳跃游戏

 

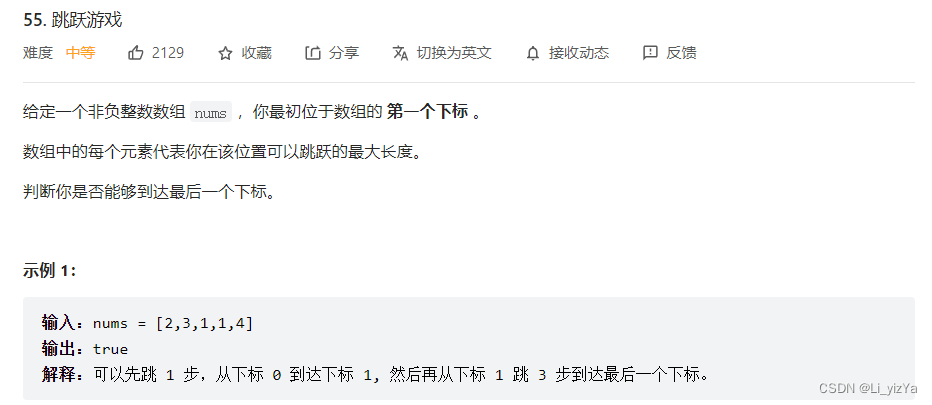
解题思路：贪心思想，遍历nums数组，如果可以到达该位置，则根据在该位置可以跳跃的长度更新最大可到达位置，如果最大可到达位置大于nums的长度，则返回true，反之遍历结束后返回false。heb

class Solution {
    public boolean canJump(int[] nums) {
        int rightMost = 0;
        for (int i = 0; i < nums.length; i++) {
            if (i <= rightMost) {
                rightMost = Math.max(i + nums[i], rightMost);
                if (rightMost >= nums.length - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

合并区间

题目链接：56. 合并区间

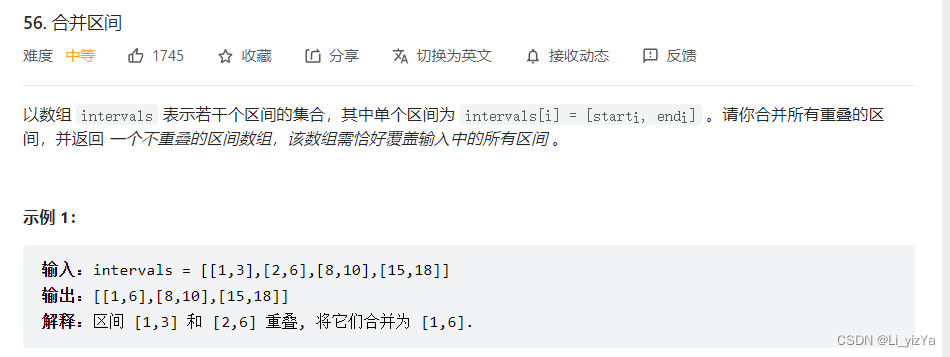
解题思路：首先对给出的区间按照左边界值进行从小到大的排序， 之后根据每一个区间的左边界和右边界来确定是新增一个区间还是更新当前区间的右边界值。

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
        List<int[]> merged = new ArrayList<>();
        for (int i = 0; i < intervals.length; i++) {
            int l = intervals[i][0];
            int r = intervals[i][1];
            if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < l) {
                merged.add(new int[]{l, r});
            } else {
                merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], r);
            }
        }
        return merged.toArray(new int[merged.size()][]);
    }
}

不同路径 

题目链接：62. 不同路径

 

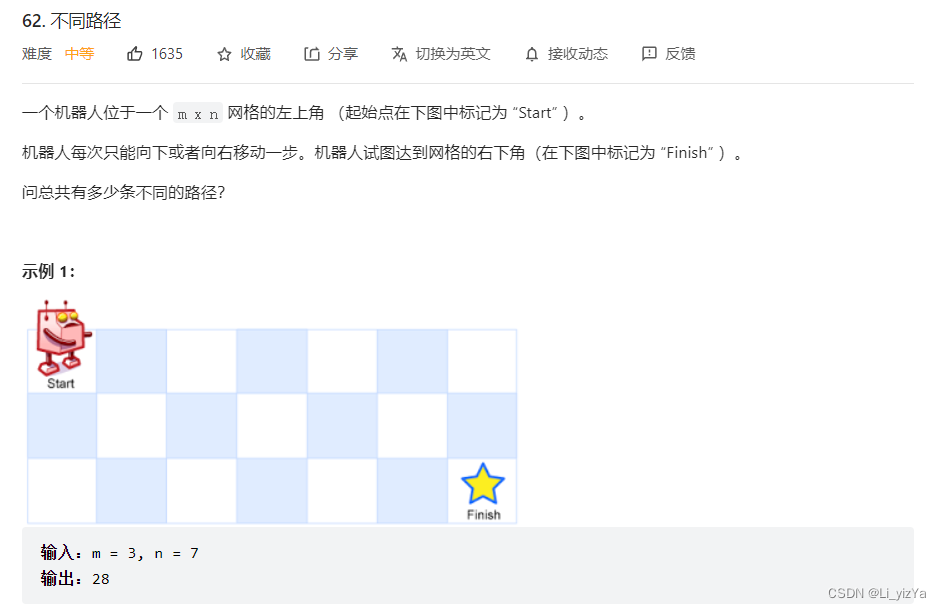
解题思路：动态规划思想，列出动态规划的状态、状态方程、初始值即可

    状态定义：f(i, j): 从(0, 0)到(i, j)的路径总数

    状态方程：f(i, j) = f(i - 1, j) + f(i, j - 1)

    初始化：f(i, 0) = 1, f(0, i) = 1

    返回值：f(m - 1, n - 1)

class Solution {
    /**
    状态定义：f(i, j): 从(0, 0)到(i, j)的路径总数
    状态方程：f(i, j) = f(i - 1, j) + f(i, j - 1)
    初始化：f(i, 0) = 1, f(0, i) = 1
    返回值：f(m - 1, n - 1)
     */
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++) {
            dp[i][0] = 1;
        } 
        for (int i = 0; i < n; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

最小路径和 

题目链接：64. 最小路径和

 

解题思路：动态规划思想，列出动态规划的状态、状态方程、初始值即可

    状态定义：f(i, j): 从(0, 0)到(i, j)的最小路径和
    状态方程：f(i, j) = min(f(i - 1, j), f(i, j - 1)) + grid[i][j]
    初始值：f(0, i) = grid[0][i] + f(0, i - 1), f(i, 0) = grid[i][0] + f(i - 1, 0) 
    返回值：f(m - 1, n - 1) 

class Solution {
    /**
    状态定义：f(i, j): 从(0, 0)到(i, j)的最小路径和
    状态方程：f(i, j) = min(f(i - 1, j), f(i, j - 1)) + grid[i][j]
    初始值：f(0, i) = grid[0][i] + f(0, i - 1), f(i, 0) = grid[i][0] + f(i - 1, 0) 
    返回值：f(m - 1, n - 1)
     */
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < n; i++) {
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        }
        for (int i = 1; i < m; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

爬楼梯 

题目链接：70. 爬楼梯

 

解题思路：简单的动态规划问题，由于每次只能跳一个或两个台阶，所以第i阶只能从第i-1阶或者第i-2阶跳上来，因此可以得出状态方程为：f(i) = f(i - 1) + f(i - 2)

    状态定义：f(i): 从0阶到达i阶的跳跃方法数

    状态方程：f(i) = f(i - 1) + f(i - 2)

    初始化：f(0) = 1, f(1) = 2 f(0)代表第一阶，f(1)代表第二阶

    返回值：f(n - 1)

 

class Solution {
    /**
    状态定义：f(i): 从0阶到达i阶的跳跃方法数
    状态方程：f(i) = f(i - 1) + f(i - 2)
    初始化：f(0) = 1, f(1) = 2 f(0)代表第一阶，f(1)代表第二阶
    返回值：f(n - 1)
     */
    public int climbStairs(int n) {
        if (n <= 2) {
            return n;
        }
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n - 1];
    }
}

颜色分类

题目链接：75. 颜色分类

 

解题思路：双指针思想，用指针p0来交换0， 指针p1来交换1，遍历数组，如果找到了1，将其与nums[p1]交换，交换结束后p1++；如果找到了0，则先将其与nums[p0]交换，交换结束后判断p0与p1的大小，如果p1大于p0，则将nums[p1]与nums[i]再进行交换，交换结束后p0++，p1++。

例如2，0，2，1，1，0，再经过几次遍历交换后，此时数组的值为0，1，1，2，2，0，此时p0 = 1，p1 = 3，此时i = 5， 首先将i与p0的值进行交换，交换结束后为0，0，1，2，2，1，此时再将i与p1的值进行交换，就得到最终结果0，0，1，1，2，2

class Solution {
    public void sortColors(int[] nums) {
        int n = nums.length;
        int p0 = 0;
        int p1 = 0;
        for (int i = 0; i < n; i++) {
            if (nums[i] == 1) {
                swap(nums, i, p1);
                p1++;
            } else if (nums[i] == 0) {
                swap(nums, i, p0);
                if (p0 < p1) {
                    swap(nums, i, p1);
                }
                p0++;
                p1++;
            }
        }
    }
    private void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}

子集

题目链接：78. 子集

 

解题思路：回溯思想，当cur == nums.length时，说明深度优先搜索已经走到了尽头，此时就将当前结果加入结果集中，将每一种可能都尝试一遍即可

class Solution {
    List<List<Integer>> ret = new ArrayList<>();
    List<Integer> curRet = new ArrayList<>();
    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ret;
    }
    private void dfs(int cur, int[] nums) {
        if (cur == nums.length) {
            ret.add(new ArrayList<Integer>(curRet));
            return;
        }
        curRet.add(nums[cur]);
        dfs(cur + 1, nums);
        curRet.remove(curRet.size() - 1);
        dfs(cur + 1, nums);
    }
}

单词搜索

题目链接：79. 单词搜索

 

解题思路：回溯思想，先在网格中找到单词的第一个字符，之后开始对其上下左右进行查找，看是否存在第二个字符，如果存在则继续判断，反之返回false。由于本题规定不允许字母重复使用，因此定义一个标记数组visited，已经使用过的字母设为1，未使用过的设为0，注意在搜索结束后需要将标记数组置为0. 

class Solution {
    public boolean exist(char[][] board, String word) {
        int m = board.length;
        int n = board[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (board[i][j] == word.charAt(0)) {
                   int[][] visited = new int[m][n]; 
                   if (dfs(board, word, visited, 0, i, j)) {
                       return true;
                   }
                }
            }
        }
        return false;
    }
    private boolean dfs(char[][] board, String word, int[][] visited, int index, int i, int j) {
        if (index == word.length()) {
            return true;
        }
        //判断是否越界
        if (i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word.charAt(index) || visited[i][j] == 1) {
            return false;
        }
        if (board[i][j] == word.charAt(index)) {
            visited[i][j] = 1;
            index++;
        }
        boolean ret = false;
        if (dfs(board, word, visited, index, i + 1, j)
            || dfs(board, word, visited, index, i - 1, j)
            || dfs(board, word, visited, index, i, j + 1)
            || dfs(board, word, visited, index, i, j - 1)
        ) {
            ret = true;
        }
        visited[i][j] = 0;
        return ret;
    }
}

二叉树的中序遍历 

题目链接：94. 二叉树的中序遍历

递归

class Solution {
    List<Integer> ret = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if (root == null) {
            return ret;
        }
        inorder(root);
        return ret;
    }
    private void inorder(TreeNode root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        ret.add(root.val);
        inorder(root.right);
    }
}

非递归：利用栈的特性来实现二叉树的中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret = new ArrayList<>();
        if (root == null) {
            return ret;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        while (node != null || !stack.isEmpty()) {
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            ret.add(node.val);
            node = node.right;
        }
        return ret;
    }
}

不同的二叉搜索树 

题目链接：96. 不同的二叉搜索树

 

class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }
        return dp[n];
    }
}