Hi,你好。我是茶桁。
在上一节课讲SVM之后,再给大家将一个新的分类模型「决策树」。我们直接开始正题。
决策树
我们从一个例子开始,来看下面这张图:

假设我们的x1 ~ x4是特征,y是最终的决定,打比方说是买东西和不买东西,0为不买,1为买东西,假设现在y是[0,0,1,0,1]。
那么,我们应该以哪个特征为准去判断到底y是0还是1呢?
如果关注x3,那么x3为A的时候,即有0也有1,我们先放一边找找看有没有更合适的。
如果是x4的话,肉眼可见的,区分度是最准确的对吧?B的都是都是0,C的时候都是1,那么x4也就是区分度最大的。
我们现在换成人的思维过程来说,肯定是期望先找到那个最能区分它的,就是最能识别的特征。这个最能识别的特征在数学里面有一个专门的定义:Salient feature, 就是显著特征。
如果我们更改一下x4的值,变成[B,C,C,B,B], 那x4也就不那么显著了。这个时候最能区分的就是x2了,只在x2[1]的位置上判断错了一个。
这个时候,我们就需要客观的衡量一下,什么叫做最能区分,或者说是最能分割,最显著的区别。这就需要一个专门的数值来计算。
那我们就来看看,到底怎么样来做区分。我们现在根据一个值,将我们的数据分成了两堆,那咱们的期望就是这两堆数据尽可能是一样的。比如极端情况下,一堆全是0, 一堆全是1,当然,中间混进去一个不一样的也行,但是尽可能的「纯」:

好,那我们该怎么定义这个「纯」呢?
我们大家应该都知道物理里有一个定义:「熵」,那熵在物理里是衡量物体的混乱程度的。
比如说一个组织、一个单位、公司或者个人,其内部的熵都是在呈现越来越混乱,而且熵的混乱具有不可逆性。这个呢,就是熵增定律,也叫「热力学第二定律」。是德国人克劳修斯提出的理论,最初用于揭示事物总是向无序的方向的发展、以及“孤立系统下热量从高温物体流向低温不可逆”的热力学定律(要不说看我的文章涨学问呢是吧)。
信息熵
好,说回咱们的机器学习。后来有一个叫「香农」的人要衡量一堆新息的混乱程度,就起了一个名字「信息熵」,也就成了衡量信息的复杂程度。
那么信息熵怎么求呢?
E n t r o p y = ∑ i = 1 n − p ( c i ) l o g 2 ( p ( c i ) ) \begin{align*} Entropy = \sum_{i=1}^n-p(c_i)log_2(p(c_i)) \end{align*} Entropy=i=1∑n−p(ci)log2(p(ci))
这个值越大,就说明了这个新息越混乱,相反的,越小就说明越有秩序。来,我们看一下代码演示,定义一个熵的方法:
import numpy as np
from icecream import ic
from collections import Counter
def pr(e, elements):
counter = Counter(elements)
return counter[e] / len(elements)
# 信息熵
def entropy(elements):
return -np.sum(pr(e, element) * np.log(pr(e, elements)) for e in elements)
然后我们具体的来看几组数据:
ic(entropy([1,1,1,1,1,0]))
ic(entropy([1,1,1,1,1,1]))
ic(entropy([1,2,3,4,5,8]))
ic(entropy([1,2,3,4,5,9]))
ic(entropy(['a','b','c','c','c','c','c']))
ic(entropy(['a','b','c','c','c','c','d']))
---
ic| entropy([1,1,1,1,1,0]): 1.05829973151282
ic| entropy([1,1,1,1,1,1]): -0.0
ic| entropy([1,2,3,4,5,8]): 1.7917594692280547
ic| entropy([1,2,3,4,5,9]): 1.7917594692280547
ic| entropy(['a','b','c','c','c','c','c']): 1.7576608876629927
ic| entropy(['a','b','c','c','c','c','d']): 2.1130832934475294
我们可以看到,最「纯」的是第二行数据,然后是第一行,第三行和第四行是一样的。5,6行就更混乱一些。
那接下来的知识点是只关于Python的,我们看上面的代码是不是有点小问题?这个代码里有很多的冗余。一般情况下,会将counter改成全局变量,但是一般如果想要代码质量好一些,尽量不要轻易定义全局变量。我们来简单的修改一下:
def entropy(elements):
# 信息熵
def pr(es):
counter = Counter(es)
def _wrap(e):
return counter[e] / len(elements)
return _wrap
p = pr(elements)
return -np.sum(p(e) * np.log(p(e)) for e in elements)
这样写之后,我们再用刚才的数据来进行调用会看到结果完全一样。不过如果这样写之后,如果我们数据量很大的情况下,会发现会快很多。
Gini系数
除了上面这个信息熵之外,还有一个叫Gini系数,和信息熵很类似:
G i n i = 1 − ∑ i = 1 n p 2 ( C i ) \begin{align*} Gini = 1 - \sum_{i=1}^np^2(C_i) \\ \end{align*} Gini=1−i=1∑np2(Ci)
假如说probability都是1,也就是最纯的情况,那么1减去1就等于0。如果它特别长,特别混乱,都很分散,那probability就会越接近于0,那么1减去0,那结果也就是越接近于1。
那么代码实现一下就是这样:
def geni(elements):
return 1-np.sum(pr(e) ** 2 for e in set(elements))
好吧,这个时候我发现一个问题,之前我们将probability函数定义到熵函数内部了,为了让Gini函数能够调用,我们还得拿出来。在我们之前修改的初衷不变的情况下,我们来这样进行修改:
def pr(es):
counter = Counter(es)
def _wrap(e):
return counter[e] / len(es)
return _wrap
def entropy(elements):
# 信息熵
p = pr(elements)
return -np.sum(p(e) * np.log(p(e)) for e in elements)
哎,这样就对了。优雅…
然后我们来修改Gini函数,让其调用pr函数:
def gini(elements):
p = pr(elements)
return 1 - np.sum(p(e) ** 2 for e in set(elements))
然后我们写一个衡量的方法:
pure_func = gini
然后我们将之前的调用都修改一下:
ic(pure_func([1,1,1,1,1,0]))
ic(pure_func([1,1,1,1,1,1]))
ic(pure_func([1,2,3,4,5,8]))
ic(pure_func([1,2,3,4,5,9]))
ic(pure_func(['a','b','c','c','c','c','c']))
ic(pure_func(['a','b','c','c','c','c','d']))
---
ic| pure_func([1,1,1,1,1,0]): 0.2777777777777777
ic| pure_func([1,1,1,1,1,1]): 0.0
ic| pure_func([1,2,3,4,5,8]): 0.8333333333333333
ic| pure_func([1,2,3,4,5,9]): 0.8333333333333333
ic| pure_func(['a','b','c','c','c','c','c']): 0.44897959183673464
ic| pure_func(['a','b','c','c','c','c','d']): 0.6122448979591837
我们可以看到,Gini系数是把整个纯度压缩到了0~1之间,越接近于1就是越混乱,越接近0呢就是越有秩序。
其实除了数组之外,字符串也是一样可以衡量的:
ic(pure_func("probability"))
ic(pure_func("apple"))
ic(pure_func("boom"))
---
ic| pure_func("probability"): 0.8760330578512396
ic| pure_func("apple"): 0.72
ic| pure_func("boom"): 0.625
在能够定义纯度之后,现在如果我们有很多数据,就比方说是我们最之前定义数据再增多一些:[x1, x2, x3, ..., xn],那么我们决策树会做什么呢?
根据x1对y做了分类,根据x2对y做了分类,做了分类之后,通过x1把y分成了两堆,一堆我们称呼其为m_left, 另外一堆我们称呼其为m_right,然后我们来定义一个loss函数:
l o s s = m l e f t n ⋅ G l e f t + m r i g h t m ⋅ G r i g h t \begin{align*} loss = \frac{m_{left}}{n} \cdot G_{left} + \frac{m_{right}}{m} \cdot G_{right} \end{align*} loss=nmleft⋅Gleft+mmright⋅Gright
现在要让这个loss函数的值最小。在整个式子中,G代表的是纯度函数,这个纯度函数可以是Entropy,也可以是Gini。
loss函数的值最小的时候,就可以实现左右两边分的很均匀。我们把这个算法就叫做CART。

CART算法其实就是classification and regression tree Algorithm, 也称为「分类和回归树算法」。
上面我们讲的所有内容可以实现分类问题,那么回归问题怎么解决呢?CART里可是包含了Regression的。
好,还是我们最之前给的数据,我们现在的y不是[0,0,1,0,1]了,我们将其更改为[1.3,1.4,0.5,0.8,1.9]。我们人类大脑中的直觉会怎么分类?会将[1.3,1.4,1.9]分为一类,而[0.5,0.8]分为一类对吧?(我说的是大部分人,少部分「天才」忽略)。
那么为了完成这样的一个分类,我们将之前公式里的纯度函数替换成MSE,那么函数就会变成如下这个样子:
J ( k , t k ) = m l e f t m ⋅ M S E l e f t + m r i g h t m M S E r i g h t J(k, t_k) = \frac{m_{left}}{m} \cdot MSE_{left} + \frac{m_{right}}{m}MSE_{right} J(k,tk)=mmleft⋅MSEleft+mmrightMSEright
MSE是什么呢?其实就是均方误差。
M S E n o d e = ∑ i ∈ n o d e ( y ^ n o d e − y ( i ) ) 2 y ^ n o d e = 1 m n o d e ∑ i ∈ n o d e y ( i ) \begin{align*} MSE_{node} & = \sum_{i \in node}(\hat y_{node} - y^{(i)})^2 \\ \hat y_{node} & = \frac{1}{m_{node}}\sum_{i\in node}y^{(i)} \end{align*} MSEnodey^node=i∈node∑(y^node−y(i))2=mnode1i∈node∑y(i)
我们要取的,就是最小的那一个MSE。
决策树最大的优点就是在决策上我们需要更大的解释性的时候很直观,决策树可以将其分析过程以树的形式展现出来。一般在商业、金融上进行决策的时候我们都需要很高的解释性。就比如下面这个例子:
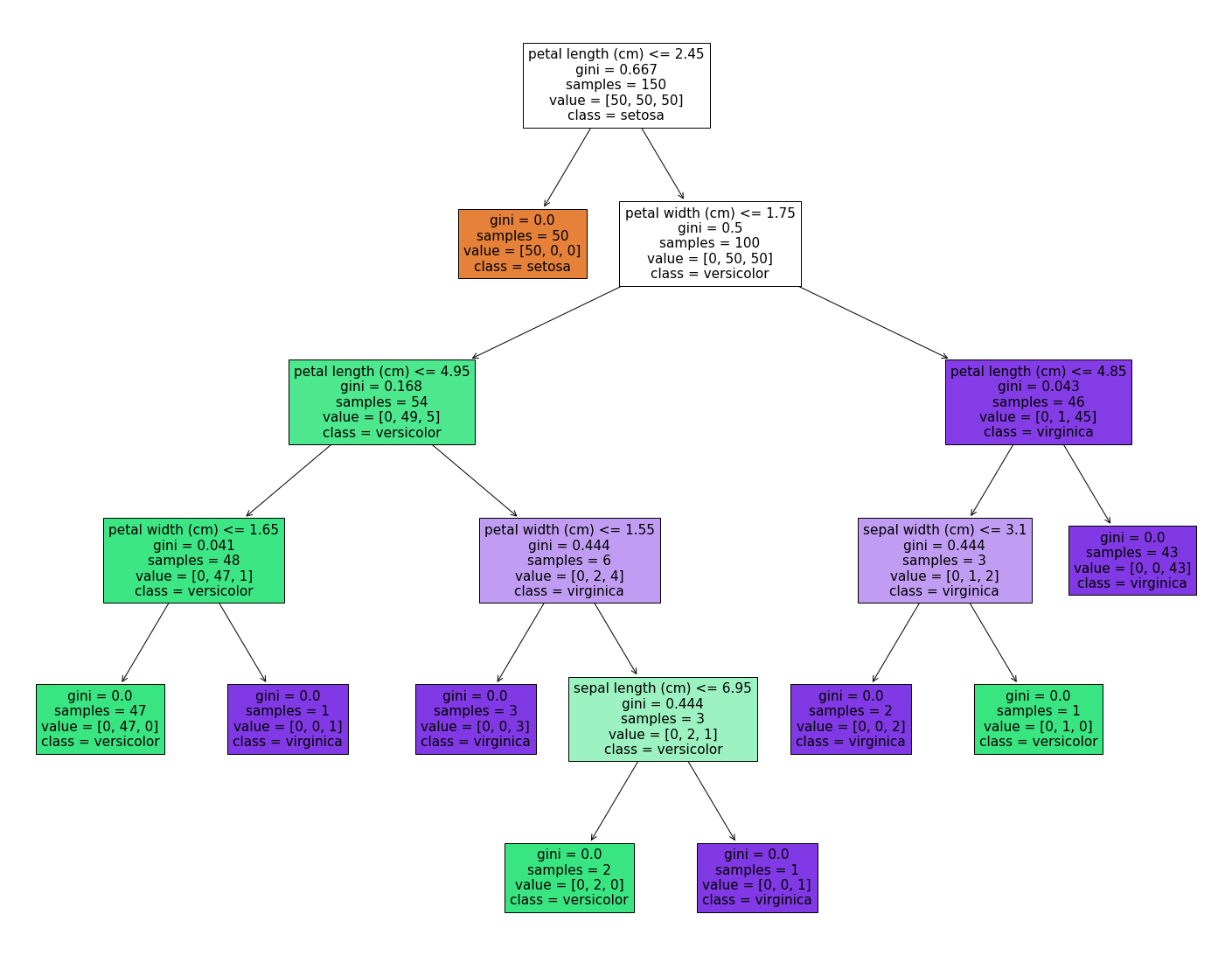
第二呢,它可以来提取重要特征。决策术可能某一类问题上效果假设最多只能做到85%的准确度,我们期望换一种模型,希望用到的维度少一点。
比方说要做逻辑回归,我们期望的w.x+b乘以一个Sigmoid,原来的x是10维的,我们期望把它降到5维。那这个时候决策树的构建过程就从最显著的特征开始逐渐构建,我们就可以把它前五个特征给他保留下来,前五个特征就是最salience的feature。我们假如把它用到逻辑回归上,直接用这五个维度就可以了。
接着我们来个问题:本来是10维的我们期望把它变成5维,为什么我们希望降维呢?
还记得我们「拟合」这一节么?我们说过,过拟合最主要的原因是数据量过少或者模型过于复杂,那为什么数据量过少呢?不知道是否还记得我讲过的维度灾难。
多个维度就需要多个数量级的数据。在仅有这么多数据的情况下,维度越多需要更多数据来拟合,但是大部分时候我们并没有那么多数据。
这个问题其实是一个很经典的问题,为什么我们做各种机器学习的时候期望降维。如果能把这个仔仔细细的想清楚,其实机器学习原理基本上已经能够掌握清楚了。
接下来我们再说说它的缺点,其实也很明显,它的分类规则太过于简单。所以它最大的缺点就是因为简单,所以好解释,但正是因为简单,所以解决不了复杂问题。
和SVM一样,也可以给决策树加核函数,曾经有一段时间这也是很重要的一个研究领域。
好,在结束之前我们预告一下下一节课内容,我们还是讲决策树,讲讲决策树中的Adaboost等,以及决策树的升级版:随机森林。