目录

使用BFS求解单源路径问题

BFS重要性质

无权图的最短路径问题

---

使用BFS求解单源路径问题

import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Queue;

public class SingleSourcePath {

    private Graph G;
    private int s;//在SingleSourcePath中传入的源

    private boolean[] visited;
    private int[] pre;

    public SingleSourcePath(Graph G, int s){

        this.G = G;
        this.s = s;

        visited = new boolean[G.V()];
        pre = new int[G.V()];//图有多少个顶点就开多少空间
        for(int i = 0; i < pre.length; i ++)
            pre[i] = -1;

        bfs(s);//从s到其他连通分量是不可达的
    }

    private void bfs(int s){

        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        pre[s] = s;
        while(!queue.isEmpty()){
            int v = queue.remove();

            for(int w: G.adj(v))
                if(!visited[w]){
                    queue.add(w);
                    visited[w] = true;
                    pre[w] = v;//w的上一个顶点是v
                }
        }
    }

    public boolean isConnectedTo(int t){
        G.validateVertex(t);//看用户传入的t是否合法
        return visited[t];//若t被遍历到了，说明t和s属于同一个连通分量，从s肯定有条路径到达t
    }

    public Iterable<Integer> path(int t){

        ArrayList<Integer> res = new ArrayList<Integer>();
        if(!isConnectedTo(t)) return res;//若从s无法到达t则返回一个空的ArrayList，说明没有路径能从s到t

        int cur = t;
        while(cur != s){
            res.add(cur);
            cur = pre[cur];
        }
        res.add(s);

        Collections.reverse(res);//把ArrayList所有元素颠倒出来成为正序
        return res;
    }

    public static void main(String[] args){

        Graph g = new Graph("g.txt");//用户自己传入的图
        SingleSourcePath sspath = new SingleSourcePath(g, 0);
        System.out.println("0 -> 6 : " + sspath.path(6));
    }
}

BFS重要性质

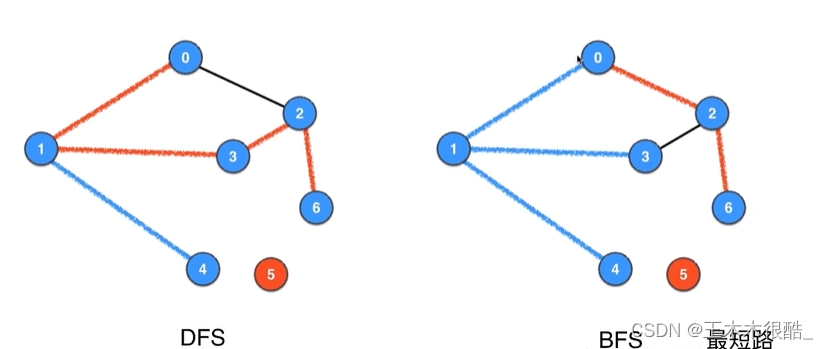
BFS求解的路径不是一般路，而是最短路，而且要注意BFS求最短路径必须是无权图！ 广度优先遍历先遍历离源顶点近的，先遍历的顶点的距离小于等于后遍历的顶点离源顶点的距离。其实这个和树的广度优先遍历的顺序是一模一样的。

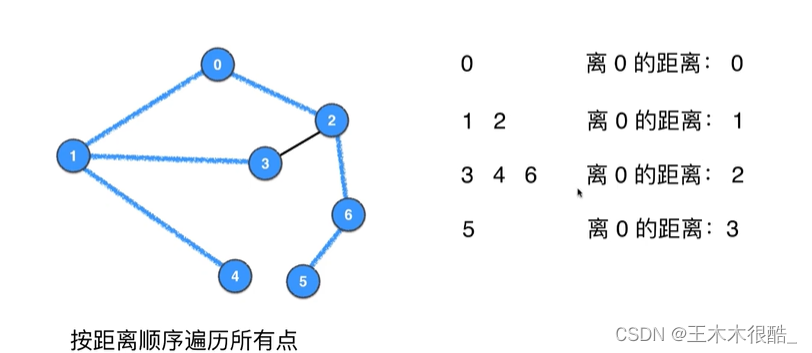
无权图的最短路径问题

用一个dis数组来记录距离。

import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Queue;

// Unweighted Single Source Shortest Path
public class USSSPath {

    private Graph G;
    private int s;

    private boolean[] visited;
    private int[] pre;
    private int[] dis;

    public USSSPath(Graph G, int s){

        this.G = G;
        this.s = s;

        visited = new boolean[G.V()];
        pre = new int[G.V()];
        dis = new int[G.V()];
        for(int i = 0; i < G.V(); i ++) {
            pre[i] = -1;
            dis[i] = -1;
        }
        bfs(s);

        for(int i = 0; i < G.V(); i ++)
            System.out.print(dis[i] + " ");
        System.out.println();
    }

    private void bfs(int s){

        Queue<Integer> queue = new LinkedList<>();
        queue.add(s);
        visited[s] = true;
        pre[s] = s;
        dis[s] = 0;
        while(!queue.isEmpty()){
            int v = queue.remove();

            for(int w: G.adj(v))
                if(!visited[w]){
                    queue.add(w);
                    visited[w] = true;
                    pre[w] = v;
                    dis[w] = dis[v] + 1;
                }
        }
    }

    public boolean isConnectedTo(int t){
        G.validateVertex(t);
        return visited[t];
    }

    public int dis(int t){
        G.validateVertex(t);
        return dis[t];//返回从源点到某个目标顶点的长度
    }

    public Iterable<Integer> path(int t){

        ArrayList<Integer> res = new ArrayList<Integer>();
        if(!isConnectedTo(t)) return res;

        int cur = t;
        while(cur != s){
            res.add(cur);
            cur = pre[cur];
        }
        res.add(s);

        Collections.reverse(res);
        return res;
    }

    public static void main(String[] args){

        Graph g = new Graph("g.txt");
        USSSPath ussspath = new USSSPath(g, 0);
        System.out.println("0 -> 6 : " + ussspath.path(6));
        System.out.println("0 -> 6 : " + ussspath.dis(6));
    }
}