代码随想录复习
文章目录
- 代码随想录复习
- 209.长度最小的子数组(滑动窗口)
- 76.最小覆盖子串
- 904.水果成篮
- 59.螺旋矩阵2
- 螺旋矩阵1
209.长度最小的子数组(滑动窗口)
209.长度最小的子数组
复习一下滑动窗口,滑窗的复杂度还是O(n)的,等于说拿r 遍历了一下数组
首先,滑动窗口的板子
for r in range(len()):
(在r滑动过程中,更新一下要维护的变量)
while l <= r and 滑窗移动的条件:
首先更新一下要维护的变量
l += 1 (滑窗左边界右移动)
按着板子这道题应该能秒杀因为很简单
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
l, r = 0, 0
sum = 0
length = len(nums)+1
for r in range(len(nums)):
sum += nums[r]
while l <= r and sum >= target:
length = min(length, r-l+1)
sum -= nums[l]
l += 1
return length if length != len(nums)+1 else 0
76.最小覆盖子串
76.最小覆盖子串
t字符串中每一位的数量达标,并且总体数量达标,窗口右移
所以需要一个t_wordict和一个总需求flag 参与控制窗口右移
具体的更新窗口变量的逻辑在代码对应部分有所体现
class Solution:
def minWindow(self, s: str, t: str) -> str:
l, r = 0, 0
t_wordict = collections.Counter(t)
flag = len(t)
min_len = len(s) + 1
start, end = 0, -1
for r in range(len(s)):
ch = s[r]
if ch in t_wordict:
if t_wordict[ch] > 0: flag -= 1
t_wordict[ch] -= 1
while l <= r and flag == 0:
if r-l+1 <= min_len:
min_len = r-l+1
start, end = l, r
ch = s[l]
if ch in t_wordict:
if t_wordict[ch] == 0: flag += 1
t_wordict[ch] += 1
l += 1
return s[start: end+1]
904.水果成篮
904.水果成篮
这道题需要记住的有两个点,
一个是dict可以用Counter,因为新的元素进字典不用创建,直接可以dict[‘ch’] += 1
一个是删除字典里的value值为0的元素可以用 dict.pop(‘ch’)
这道题意思是,窗口里不能出现超过两种元素,求这种窗口的最长长度。所以窗口的更新逻辑是窗口里的元素大于2,但是要注意一旦value为0,要删除它不然会占用元素个数
这道题的结果更新逻辑需要放在窗口右滑之后,因为右滑逻辑是 > 2所以不能在这个时候更新长度,需要在滑动调整之后,迭代较大的那个窗口长度值
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
l, r = 0, 0
fruits_dict = Counter()
max_length = 0
for r in range(len(fruits)):
fruits_dict[fruits[r]] += 1
while l <= r and len(fruits_dict) > 2:
fruits_dict[fruits[l]] -= 1
if fruits_dict[fruits[l]] == 0: fruits_dict.pop(fruits[l])
l += 1
max_length = max(max_length, r-l+1)
return max_length
59.螺旋矩阵2
59.螺旋矩阵2
还是先理清一下思路,这道题是转着圈去填数去模拟,那么一拿到这个题的第一反应是应该 有两种循环
思维阶梯step1:
第一种属于外层循环,控制转的圈数
通过找规律可以找到如果是22、33的话,转一圈就行,如果是44、55的话,转两圈;可以发现 外层loop = n // 2, while loop 就一圈圈的转,每转一圈 loop-1
如果n是奇数的话,需要最后填上最后一个位置 res[mid][mid], mid = n // 2
思维阶梯step2:
第二种属于内层遍历,什么意思呢,就是每一条边怎么填。
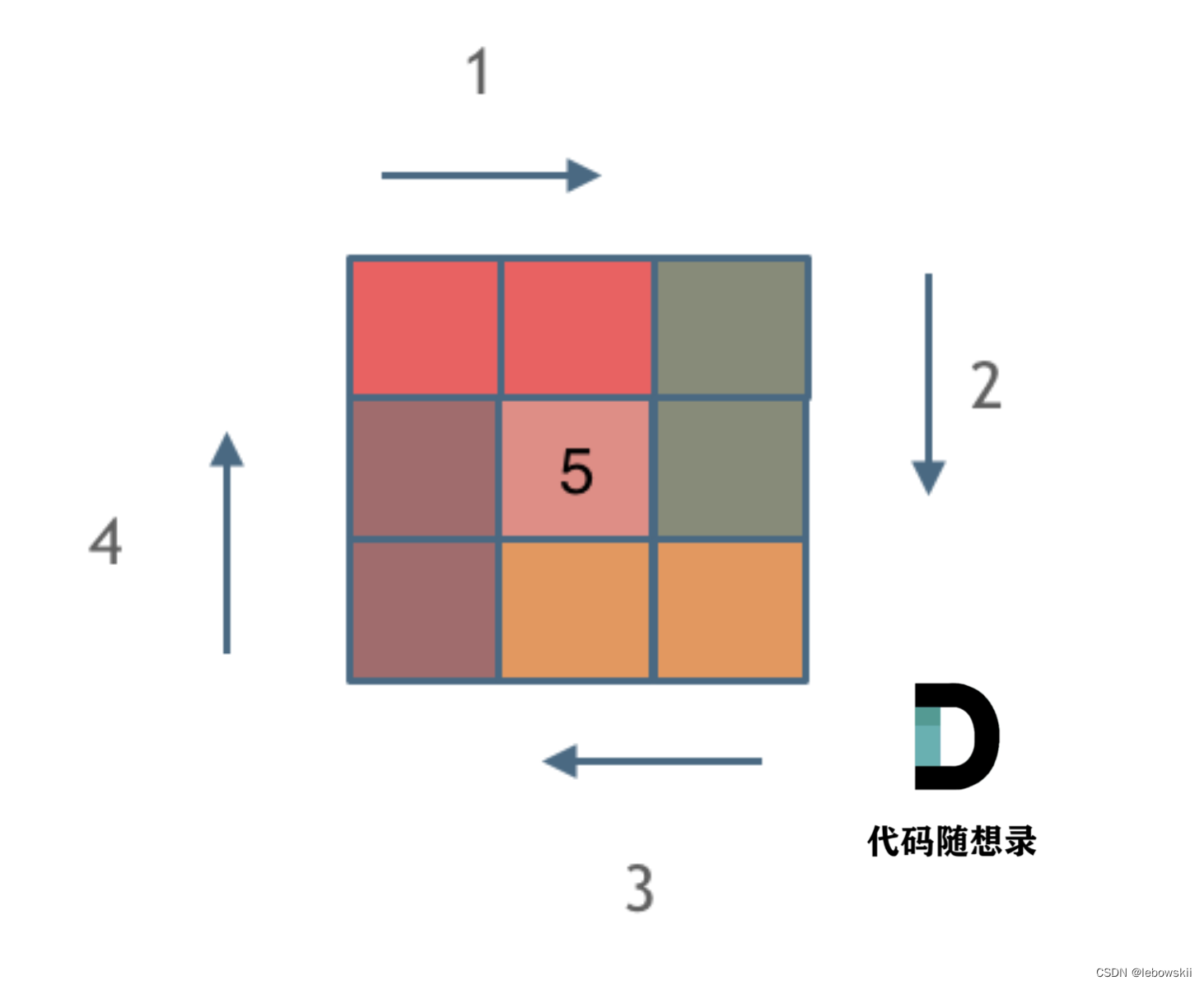
这里就需要用for了,可以看出,每一条边都坚持左闭右开的原则,这个图还不是很形象,如果是5*5的话就不一样了,每一圈loop之后,内层的for循环的开始位置和结束位置都需要移动一位,我们用startx, starty,表示横行和列的循环开始,一开始初始化为0从头开始;结束位置可以看出都需要提前一位,我们可以整一个offset, 一开始初始化为1,结束位置就是n - offset。 每绕一圈,startx, starty, 和 offset都需要+1
思维阶梯step3:
loop也就是绕圈结束后,如果n一开始是奇数,需要手动填最后的中心
有了这三步思维阶梯,就应该能够a出来,注意, startx, starty代表的含义,我习惯y代表列,x代表行, j代表列,i代表行
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
res = [[0] * n for _ in range(n)]
loop, mid = n // 2, n // 2
startx, starty, offset = 0, 0, 1
cnt = 1
while loop:
loop -= 1
for j in range(starty, n-offset):
res[startx][j] = cnt
cnt += 1
for i in range(startx, n-offset):
res[i][n-offset] = cnt
cnt += 1
for j in range(n-offset, starty, -1):
res[n-offset][j] = cnt
cnt += 1
for i in range(n-offset, startx, -1):
res[i][starty] = cnt
cnt += 1
startx += 1
starty += 1
offset += 1
if n % 2 == 1: res[mid][mid] = cnt
return res
螺旋矩阵1
54.螺旋矩阵
不想看答案了,直接仿照螺旋矩阵2写的;这道题相比上一道,多了一些不是方阵的情况,方阵的话很容易读出来,有奇数的行列的话我加了一些特判
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m, n = len(matrix), len(matrix[0])
loop = min(m//2, n//2)
startx, starty, offset = 0, 0, 1
res = []
if m == 1: #只有一行的情况
for j in range(len(matrix[0])):
res.append(matrix[0][j])
return res
if n == 1: #有多行只有一列的情况
for i in range(len(matrix)):
res.append(matrix[i][0])
return res
while loop:
loop -= 1
for j in range(starty, n-offset):
res.append(matrix[startx][j])
for i in range(startx, m-offset):
res.append(matrix[i][n-offset])
for j in range(n-offset, starty, -1):
res.append(matrix[m-offset][j])
for i in range(m-offset, startx, -1):
res.append(matrix[i][starty])
startx += 1
starty += 1
offset += 1
#绕圈完之后的特判
if m == n and m % 2 == 1: #3*3 or 5*5这种情况
res.append(matrix[m//2][n//2])
if m != n and (m%2==1 and n%2==0 or n%2==1 and m%2==0): #3*4 or 4*3的情况
if m % 2 == 1:
for j in range(starty, n-offset+1):
res.append(matrix[m//2][j])
elif n % 2 == 1:
for i in range(startx, m-offset+1):
res.append(matrix[i][n//2])
if m != n and (m % 2 == 1 and n % 2 == 1): #3*5 or 5*3的情况
if m > n:
for i in range(startx, m-offset+1):
res.append(matrix[i][n//2])
else:
for j in range(starty, n-offset+1):
res.append(matrix[m//2][j])
return res