八数码:
在一个 3×3 的网格中,1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。
例如:
1 2 3
x 4 6
7 5 8
在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x
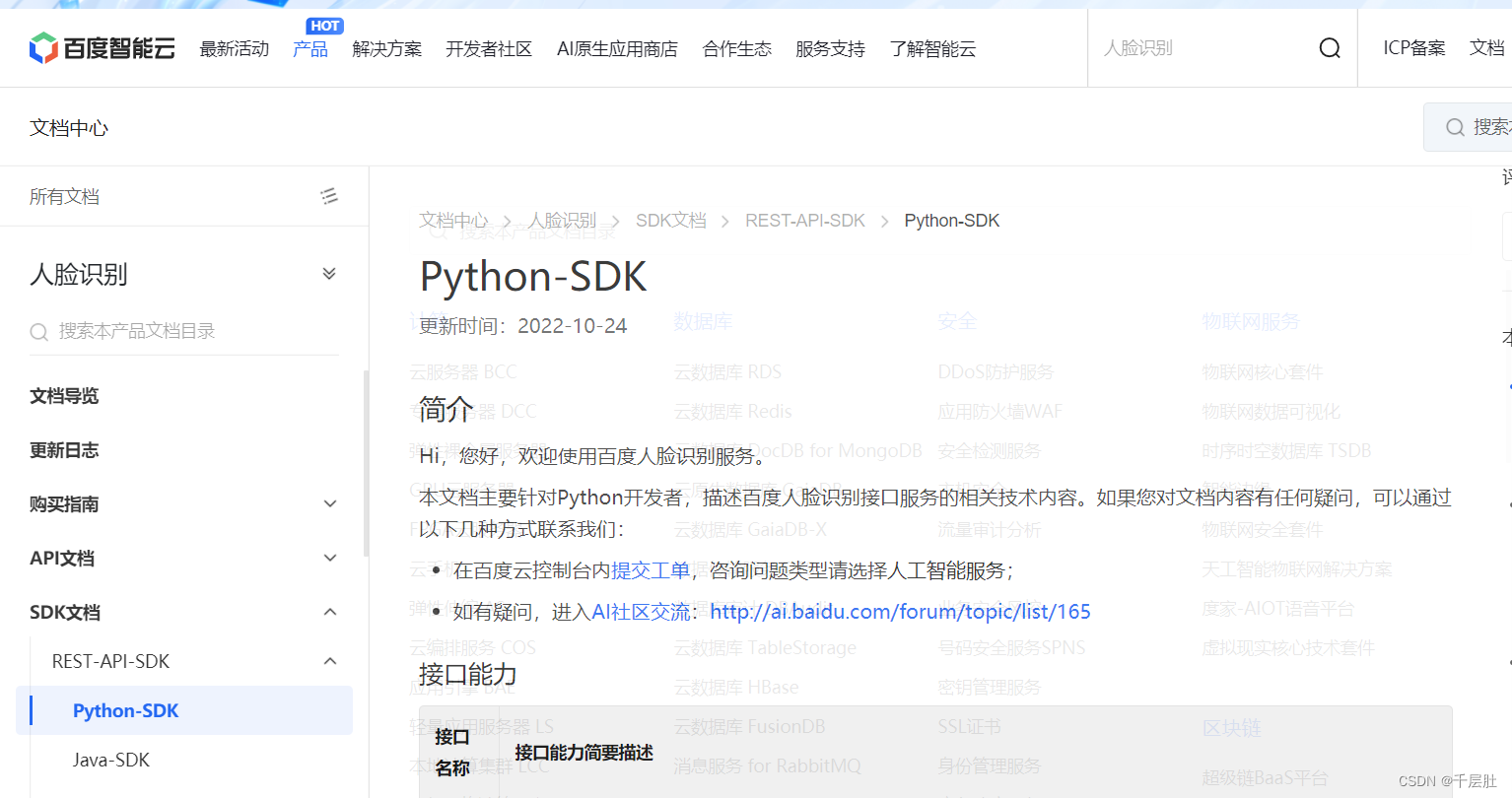
例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×3 的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8
则输入为:1 2 3 x 4 6 7 5 8
输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1
输入样例:
2 3 4 1 5 x 7 6 8
输出样例
19使用BFS求解思路:
题目要求的是3×3的矩阵八个数字,首先给一个起始状态start,然后要求通过算法,得到题目给的最终状态end。并且要求是最优解,即最短路径。
由此我们可以使用BFS即广度优先算法来解决此类问题,广度优先是层次遍历,每次通过遍历空格位置向上下左右四个方向交换,可得到四个不同的状态(边界可能小于4)以及与初始状态变化距离。
求解存在的问题:用什么数据结构来存储,该如何表示每次变化的状态,该如何记录每次状态距离初始状态的距离。
我们通过队列来记录层次遍历时每层的状态,每一层的共性就是移动距离相同。如图所示:
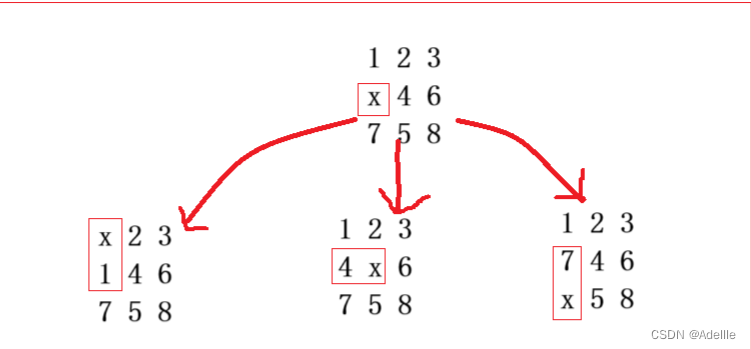
由于向左时越界所以跳过向左,由图所示,当前一共有三个状态,并且距离初始状态为1,与end状态比较不相等。
通过上面的解释,我们可以发现,使用队列来记录每次改变的状态最合适,因为队列可以按照层次遍历的顺序来存储状态,可以记录路径和搜索的顺序,并且可以帮助我们避免重复访问。然后,使用哈希表来存储每个状态对应的距离,每次要存储一次距离时,判断哈希表中是否存在当前要存储的状态,然后通过刚刚从队列中取出的状态距离加1即当前状态距离。
每次从队列中获取一个状态都要和最终状态比较,如果相等,返回hash表中对应的距离。否则通过改变空格位置来获取每次状态。如果遍历完所有的状态都没有,返回-1.
这里以JAVA为例,使用BFS算法,展示代码:
import java.sql.Statement;
import java.util.*;
class Main {
static int dx[] = {1, 0, -1, 0};
static int dy[] = {0, -1, 0, 1};//空格位置的上下左右移动
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
String start = new String();
for (int i = 0; i < 9; i++) {
char c;
c = cin.next().charAt(0);
start += c;
}
System.out.println(bfs(start));
}
private static int bfs(String start) {
String end = new String();
end = "12345678x";
Queue<String> queue = new LinkedList<>();//存储状态
Map<String, Integer> map = new HashMap<>();//每个状态到起点的位置
queue.add(start);
map.put(start, 0);
while (!queue.isEmpty()) {
String s = queue.poll();
if (s.equals(end)) return map.get(s);
int dist = map.get(s);
int k = s.indexOf("x");
int x = k / 3, y = k % 3;//二维数组中空格的下标
for (int i = 0; i < 4; i++) {//对空格进行上下左右移动
int a = x + dx[i], b = y + dy[i];
if (a >= 0 && a < 3 && b >= 0 && b < 3) {
String st = new String(swap(s.toCharArray(), k, a * 3 + b));
if (map.get(st) == null) {
map.put(st, dist + 1);
queue.add(st);
}
st = new String(swap(s.toCharArray(), k, a * 3 + b));
}
}
}
return -1;
}
private static char[] swap(char[] chars, int k, int i) {
char temp = chars[k];
chars[k] = chars[i];
chars[i] = temp;
return chars;
}
}C++代码:
#include <algorithm>
#include <iostream>
#include <unordered_map>
#include <queue>
using namespace std;
int bfs(string s)
{
queue<string>q;
unordered_map<string,int>d;
q.push(s);
d[s]=0;
string end="12345678x";
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
while(!q.empty())
{
string t=q.front();
q.pop();
if(t==end)return d[t];
int distant=d[t];
int k=t.find('x');
int x=k/3,y=k%3;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=0&&a<3&&b>=0&&b<3)
{
swap(t[k],t[a*3+b]);
if(!d.count(t))
{
d[t]=distant+1;
q.push(t);
}
swap(t[k],t[a*3+b]);
}
}
}
return -1;
}
int main()
{
string s;
for(int i=0;i<9;i++)
{
char a;
cin>>a;
s+=a;
}
cout<<bfs(s);
return 0;
}在广度优先遍历算法中,我们发现在找到最终答案之前它遍历了所有状态的八数码(盲目式搜索),对于有明确终点的问题来说,其实可以优先考虑具有较小估计代价的状态来进行搜索以尽快找到解决方案。
A*算法:
A*算法(A-star algorithm)是一种启发式搜索算法,常用于解决图形和网络中的最短路径问题。该算法在已知节点之间的连接关系以及每个节点的估计成本(启发函数)的基础上,通过遍历节点来找到从起点到目标节点的最优路径。
A*算法结合了Dijkstra算法和贪婪最佳优先搜索算法的特点,它维护两个值:g值和h值。其中g值表示起点到当前节点的实际代价,h值表示当前节点到目标节点的预计代价。通过合理选择启发函数,A*算法能够高效地找到最佳路径。
A*算法使用一个优先队列来存储待探索的节点,并根据f值(f = g + h)的大小进行排序。在每一次迭代中,它选择f值最小的节点进行探索,计算其邻居节点的g值和h值,并更新优先队列。当从队列中选出的节点为目标节点时,路径被找到。
A*算法在计算资源允许的情况下,通常能够找到最短路径。然而,如果启发函数不准确或者图形/网络过于复杂,A*算法可能会陷入局部最优解并无法找到全局最优解。
A*算法通过下面这个函数来计算每个节点的优先级。
![]()
其中:
- f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时,我们总会选取综合优先级最高(值最小)的节点。
- g(n) 是节点n距离起点的代价。
- h(n)是节点n距离终点的预计代价,这也就是A*算法的启发函数。关于启发函数我们在下面详细讲解。
A*算法在运算过程中,每次从优先队列中选取f(n)值最小(优先级最高)的节点作为下一个待遍历的节点。
另外,A*算法使用两个集合来表示待遍历的节点,与已经遍历过的节点,这通常称之为open_set和close_set。
A*算法解决八数码问题:
1. 定义状态表示:将八数码问题中的每个状态表示为一个3x3的矩阵,空白格用0表示。例如,初始状态为:
1 2 3
x 4 6
7 5 8
2. 定义启发函数:根据当前状态和目标状态之间的差异,设计一个启发函数来估计从当前状态到目标状态的代价。
3. 实现A*算法:按照以下步骤实现A*算法来解决八数码问题
算法流程图
程序设计语言编写程序,实现算法;
运行程序并对照分析不同估价函数对A*算法性能的影响。
总结
A*算法和广度优先搜索(BFS)都可以用于解决八数码问题,但它们之间存在一些重要的区别。
1. 目标导向性:
A*算法是一种启发式搜索算法,它使用一个启发函数来估计当前状态到达目标状态的代价。它通过优先考虑具有较小估计代价的状态来进行搜索,以尽快找到解决方案。
广度优先搜索则是一种朴素的无信息搜索方法,它按照层次遍历的方式搜索问题的解空间,逐渐扩展搜索树,直到找到目标状态为止。BFS不考虑每个状态的代价,只关注解的深度。
2. 内存消耗:
A*算法通常需要维护一个优先队列来存储待扩展的状态,该队列的大小与搜索过程中生成的状态数量成正比。因此,A*算法可能会占用更多的内存空间。
广度优先搜索也需要存储搜索树中所有已生成的状态,但不需要额外的优先队列。BFS在搜索空间中逐层扩展,可能会占用较大的内存空间,尤其是当搜索树的分支因子较大时。
3. 时间复杂度:
A*算法的时间复杂度取决于启发函数的质量。在最坏情况下,A*算法的时间复杂度与状态空间的大小成指数关系。