[USACO1.5]八皇后 Checker Challenge

题目描述

一个如下的 $6\times 6$ 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列 $246135$ 来描述，第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子，如下：

行号 $123456$

列号 $246135$

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。

输入格式

一行一个正整数 $n$，表示棋盘是 $n\times n$ 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

样例 #1

样例输入 #1

6

样例输出 #1

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

提示

【数据范围】
对于 $100\%$ 的数据，$6\le n\le 13$。

题目翻译来自NOCOW。

USACO Training Section 1.5

思路

搜索框架

依次搜索row行，枚举row行的col列，如果col列满足题目条件可以放皇后，则递归下一行
题目条件
每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子
由于按每行开始枚举，那么同一行一定没有两个棋子
同一列，只需要枚举上面每一行的是否存在同一列棋子即可
斜边即：枚举上面每一行的棋子与当前尝试放的棋子在x轴的距离与y轴的距离是否相等即可判断

代码

N = 15

path = [0] * N
res = []

def check(row, col) :
    for i in range(1, row + 1) : 
        if path[i] == col : return False#检查列
        if abs(row - i) == abs(path[i] - col) : return False#检查斜边
    return True

#搜索框架：依次搜索第row行，枚举col列，把col列放上皇后，然后递归下一行
def dfs(row) :
    if row == n + 1 :
        res.append(path[:])
    for i in range(1, n + 1) :
        if not check(row, i) : continue #可行性剪枝
        path[row] = i
        dfs(row + 1)
        path[row] = 0

n = int(input())

dfs(1)

for i in range(3) :
    for j in range(1, n + 1) :
        print(res[i][j], end = " ")
    print()
print(len(res))

位运算优化

lowbit运算

首先了解一下lowbit运算，lowbit(n)定义为非负整数n在二进制表示下“最低位的1及其后边所有的0”构成的所有数值
为了实现lowbit运算，先把n取反，此时第k位变成0，第0~k - 1位都是1，再加1，此时0~k-1位都变为0，k位变为1，k + 1到最高位恰好与原来相反所以
lowbit(n) = n & (~ n + 1) = n & (-n)，因为在补码表示下~n = -1 - n
python中k进制数值字符串（k = 2，8，16）转变为十进制
int(str, k)

思路

依次搜索每一行，枚举每一列，可以放皇后的位置放下皇后，标记下一行不能同列与同斜边的位置。
有意思的是二进制运算中斜边每下移一行向右（左）移以为就能得到相应行的限制

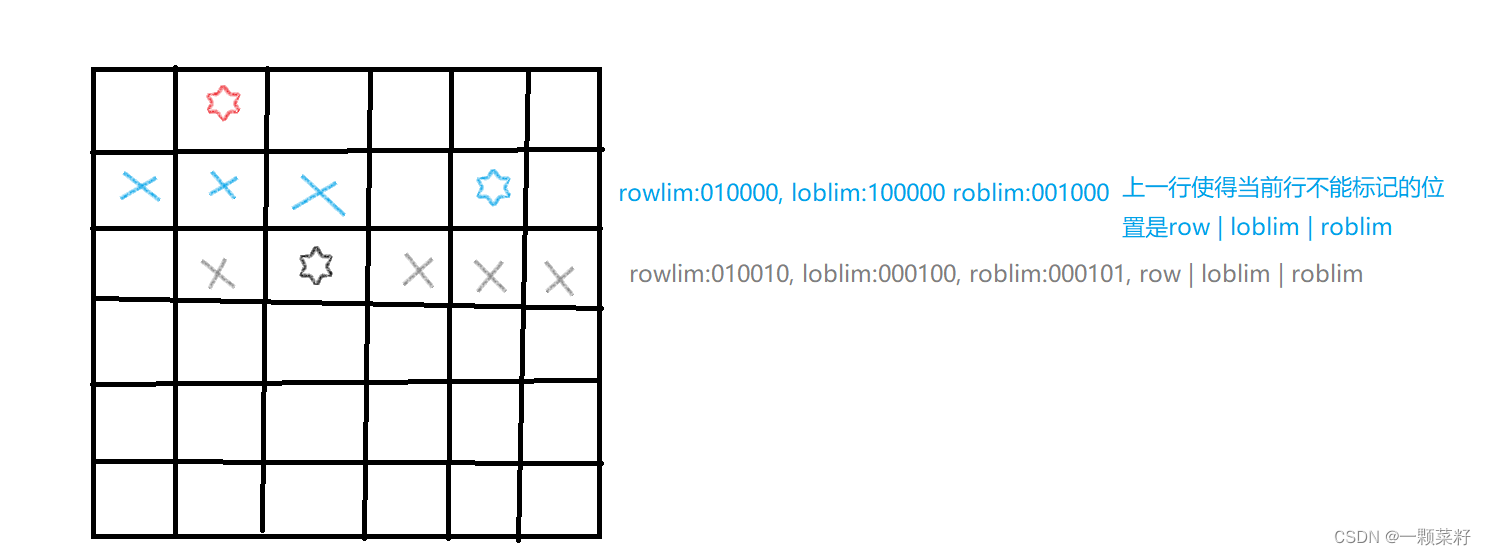
## 二进制优化

def lowbit(n) :
    return n & (-n)

path = []
res = []

def dfs(rowlim, loblim, roblim) : # 参数分别标记的是遍历到节点的当前行中那些不能在同一列列不能放，不能在同一斜边的不能放左列和右列
    if colim == n :
        res.append(path[:])
        return

    pos = n & (~(rowlim | loblim | roblim))

    while pos != 0 :
        lowb = lowbit(pos)
        path.append(len(str(bin(lowb))) - 2)
        pos -= lowb
        dfs(rowlim | lowb, (loblim | lowb) << 1, (roblim | lowb) >> 1 ) #
        path.pop()

n = (1 << int(input())) - 1

dfs(0, 0, 0)

for i in range(3) :
    for j in res[i] :
        print(j, end = " ")
    print()
print(len(res))

kkksc03考前临时抱佛脚

题目背景

kkksc03 的大学生活非常的颓废，平时根本不学习。但是，临近期末考试，他必须要开始抱佛脚，以求不挂科。

题目描述

这次期末考试，kkksc03 需要考 $4$ 科。因此要开始刷习题集，每科都有一个习题集，分别有 $s_1,s_2,s_3,s_4$ 道题目，完成每道题目需要一些时间，可能不等（$A_1,A_2,\dots ,A_{s_1}$，$B_1,B_2,\dots ,B_{s_2}$，$C_1,C_2,\dots ,C_{s_3}$，$D_1,D_2,\dots ,D_{s_4}$）。

kkksc03 有一个能力，他的左右两个大脑可以同时计算 $2$ 道不同的题目，但是仅限于同一科。因此，kkksc03 必须一科一科的复习。

由于 kkksc03 还急着去处理洛谷的 bug，因此他希望尽快把事情做完，所以他希望知道能够完成复习的最短时间。

输入格式

本题包含 $5$ 行数据：第 $1$ 行，为四个正整数 $s_1,s_2,s_3,s_4$。

第 $2$ 行，为 $A_1,A_2,\dots ,A_{s_1}$ 共 $s_1$ 个数，表示第一科习题集每道题目所消耗的时间。

第 $3$ 行，为 $B_1,B_2,\dots ,B_{s_2}$ 共 $s_2$ 个数。

第 $4$ 行，为 $C_1,C_2,\dots ,C_{s_3}$ 共 $s_3$ 个数。

第 $5$ 行，为 $D_1,D_2,\dots ,D_{s_4}$ 共 $s_4$ 个数，意思均同上。

输出格式

输出一行,为复习完毕最短时间。

样例 #1

样例输入 #1

1 2 1 3		
5
4 3
6
2 4 3

样例输出 #1

20

提示

$1\le s_1,s_2,s_3,s_4\le 20$。

$1\le A_1,A_2,\dots ,A_{s_1},B_1,B_2,\dots ,B_{s_2},C_1,C_2,\dots ,C_{s_3},D_1,D_2,\dots ,D_{s_4}\le 60$。

思路

这是一个集合题，枚举每一题，考虑每一题放在左脑还是右脑即可，依次递归

代码

s = list(map(int, input().split()))

def dfs(u, l, r) :
	global cnt
	if l >= cnt or r >= cnt : return
	if u == n :
		cnt = max(l, r)
		return
	dfs(u + 1, l + pro[u], r)
	dfs(u + 1, l, r + pro[u])

res = 0
for i in range(4) :
	n = s[i]
	pro = list(map(int, input().split()))
	cnt = 20 * 60
	dfs(0, 0, 0)
	res += cnt
print(res)

吃奶酪

题目描述

房间里放着 $n$ 块奶酪。一只小老鼠要把它们都吃掉，问至少要跑多少距离？老鼠一开始在 $(0,0)$ 点处。

输入格式

第一行有一个整数，表示奶酪的数量 $n$。

第 $2$ 到第 $(n+1)$ 行，每行两个实数，第 $(i+1)$ 行的实数分别表示第 $i$ 块奶酪的横纵坐标 $x_i,y_i$。

输出格式

输出一行一个实数，表示要跑的最少距离，保留 $2$ 位小数。

样例 #1

样例输入 #1

4
1 1
1 -1
-1 1
-1 -1

样例输出 #1

7.41

提示

数据规模与约定

对于全部的测试点，保证 $1\le n\le 15$，$|x_i|,|y_i|\le 200$，小数点后最多有 $3$ 位数字。

提示

对于两个点 $(x_1,y_1)$，$(x_2,y_2)$，两点之间的距离公式为 $\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$。

---

$\mathrm{2022.7.13}$：新增加一组 $\text{Hack}$ 数据。

思路

1、排列的方式，搜索排列中每个位置，在相应位置上枚举可放入的点，继续递归直到抵达最后一个位置
2、记忆化搜索优化，建一个记录数组f[st][i]保存经过st存储的点后从0到达i点的最短距离，搜索当前状态（一个二进制串）和当前所到达的点，枚举还没被访问过的节点，加入当前状态，更新当起点与即将访问的节点的距离（dist + 当前到达的点与即将访问点的距离），这里可以使用f数组做记忆化搜索剪枝

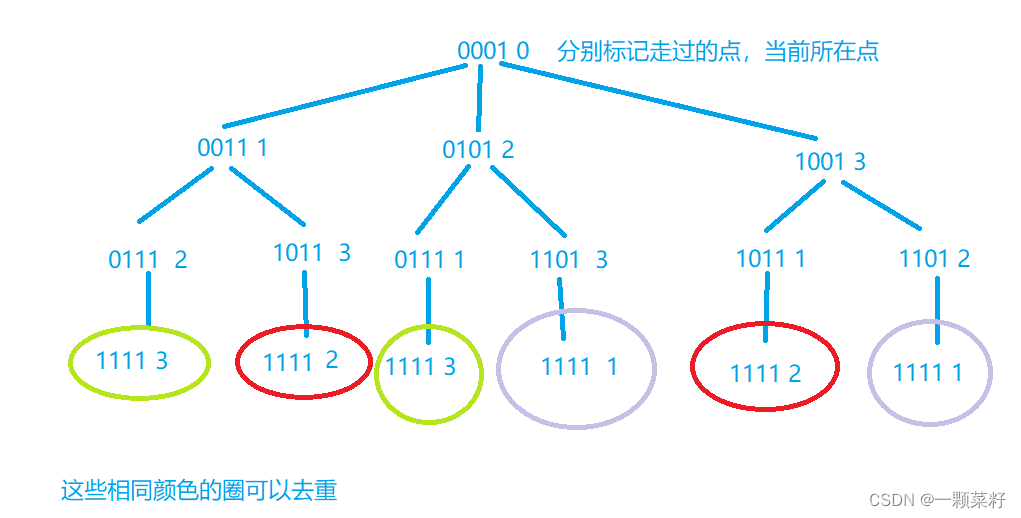
问：为何记录数组要开两维，一个记录已经走过的点，一个记录当前到达的点。
答：因为这是个排列问题，每个节点只能访问一次，只能做一次起点。如果只记录走过的点的话，则无法保证每个节点只作为起点被访问一次。

代码

朴素做法

import math
import sys
sys.setrecursionlimit(6000)
N = 16
g = []
st = [False] * N

ans = 30010.0

def ca_dist(x1, y1, x2, y2) :
    return math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)

def dfs(cnt, cab, last) :
    global ans
    if ans <= cab : return #最优性剪枝
    if cnt == n :
        ans = cab
        return
    
    for i in range(n) :
        if st[i] : continue
        st[i] = True
        dfs(cnt + 1, cab + ca_dist(last[0],last[1], g[i][0], g[i][1]), g[i])
        st[i] = False

n = int(input())

for i in range(n) :
    g.append(list(map(int, input().split())))
g.sort(reverse= True)
    
dfs(0, 0, [0, 0])

print(f"{ans :.2f}")

记忆化搜索优化

import math
import sys
sys.setrecursionlimit(6000)
N = 16
ans = 300000.0
def dfs(u, x, dist) :
    global ans
    if dist >= ans : return
    if u == edu :
        ans = dist
    for i in range(1, n + 1) :
        if st[i] : continue
        if f[u + (1 << i)][i] <= dist + w[x][i] : continue
        st[i] = True
        f[u + (1 << i)][i] = dist + w[x][i]
        dfs(u + (1 << i), i, dist + w[x][i])
        st[i] = False

n = int(input())

edu = (1 << (n + 1)) - 1

for i in range(n) :
    cheeses.append(list(map(float, input().split())))
#预处理优化
for i in range(n + 1) :
    for j in range(n + 1) :
        w[i][j] = math.sqrt((cheeses[i][0] - cheeses[j][0]) ** 2 + (cheeses[i][1] - cheeses[j][1]) ** 2)

f[1][0] = 0
dfs(1, 0, 0)
print(f"{ans:.2f}")

[USACO11OPEN]Corn Maze S

题面翻译

奶牛们去一个 $N\times M$ 玉米迷宫，$2\le N\le 300,2\le M\le 300$。

迷宫里有一些传送装置，可以将奶牛从一点到另一点进行瞬间转移。这些装置可以双向使用。

如果一头奶牛处在这个装置的起点或者终点，这头奶牛就必须使用这个装置。

玉米迷宫除了唯一的一个出口都被玉米包围。

迷宫中的每个元素都由以下项目中的一项组成：

1. 玉米，# 表示，这些格子是不可以通过的。
2. 草地，. 表示，可以简单的通过。
3. 传送装置，每一对大写字母 $\mathtt{A}$ 到 $\mathtt{Z}$ 表示。
4. 出口，= 表示。
5. 起点， @ 表示

奶牛能在一格草地上可能存在的四个相邻的格子移动，花费 $1$ 个单位时间。从装置的一个结点到另一个结点不花时间。

题目描述

This past fall, Farmer John took the cows to visit a corn maze. But this wasn’t just any corn maze: it featured several gravity-powered teleporter slides, which cause cows to teleport instantly from one point in the maze to another. The slides work in both directions: a cow can slide from the slide’s start to the end instantly, or from the end to the start. If a cow steps on a space that hosts either end of a slide, she must use the slide.

The outside of the corn maze is entirely corn except for a single exit.

The maze can be represented by an N x M (2 <= N <= 300; 2 <= M <= 300) grid. Each grid element contains one of these items:

* Corn (corn grid elements are impassable)

* Grass (easy to pass through!)

* A slide endpoint (which will transport a cow to the other endpoint)

* The exit

A cow can only move from one space to the next if they are adjacent and neither contains corn. Each grassy space has four potential neighbors to which a cow can travel. It takes 1 unit of time to move from a grassy space to an adjacent space; it takes 0 units of time to move from one slide endpoint to the other.

Corn-filled spaces are denoted with an octothorpe (#). Grassy spaces are denoted with a period (.). Pairs of slide endpoints are denoted with the same uppercase letter (A-Z), and no two different slides have endpoints denoted with the same letter. The exit is denoted with the equals sign (=).

Bessie got lost. She knows where she is on the grid, and marked her current grassy space with the ‘at’ symbol (@). What is the minimum time she needs to move to the exit space?

输入格式

第一行：两个用空格隔开的整数 $N$ 和 $M$。

第 $2\sim N+1$ 行：第 $i+1$ 行描述了迷宫中的第 $i$ 行的情况（共有$M$个字符，每个字符中间没有空格）。

输出格式

一个整数，表示起点到出口所需的最短时间。

样例 #1

样例输入 #1

5 6
###=##
#.W.##
#.####
#.@W##
######

样例输出 #1

3

提示

例如以下矩阵，$N=5,M=6$。

###=##
#.W.##
#.####
#.@W##
######

唯一的一个装置的结点用大写字母 $\mathtt{W}$ 表示。

最优方案为：先向右走到装置的结点，花费一个单位时间，再到装置的另一个结点上，花费 $0$ 个单位时间，然后再向右走一个，再向上走一个，到达出口处，总共花费了 $3$ 个单位时间。

思路

代码