一、动态规划概念

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果 [1]  。[2] 

[1]  许国根，赵后随，黄智勇．最优化方法及其MATLAB实现：许国根，赵后随，黄智勇，2018-07：91

[2]  Thomas H. Cormen,Charles E. Leiserson,Ronald L. Rivest,Clifford Stein．Introduction to Algorithms, Third Edition：麻省理工大学出版社，2009

简单理解：动态规划就是在有多个子序列作为解的时候，去寻找出最优的组合作为最优解。

二、动态规划的例子

1. 例子1：寻找两个字符串的最长公共子串？

如str_01 = '世界杯半决赛真好看'，str_02 = '决赛比半决赛更好看'

import numpy as np

def dynamic_p(s1, s2) -> list:
    r, c = len(s1), len(s2)
    dp = [[0] * (c+1) for _ in range(r+1)] #构建转移方程矩阵
    for row in range(r):
        for col in range(c):
            #转移方程表达式
            if s1[row] == s2[col]:
                dp[row+1][col+1] = dp[row][col] + 1    # 对左上角CELL值+1
            else:
                # 匹配不成功清0，这里可以不用到else，因为默认值就为0
                dp[row+1][col+1] = 0
    return dp

str_01 = '世界杯半决赛真好看'
str_02 = '决赛比半决赛更真好看'
arr = []
dp = dynamic_p(str_01, str_02)

for i in dp:
    arr.extend(i)
    print(i)                                           # 打印数组
#最长子串的位置
dp_array = np.array(dp)
res = []
for i in np.where(dp_array == np.max(dp_array))[0]:
    result = str_01[i - np.max(dp_array):i]
    res.append(result)
print(f"最长公共子串长度为:{max(arr)}")
print(f"最长公共子串为:{res}")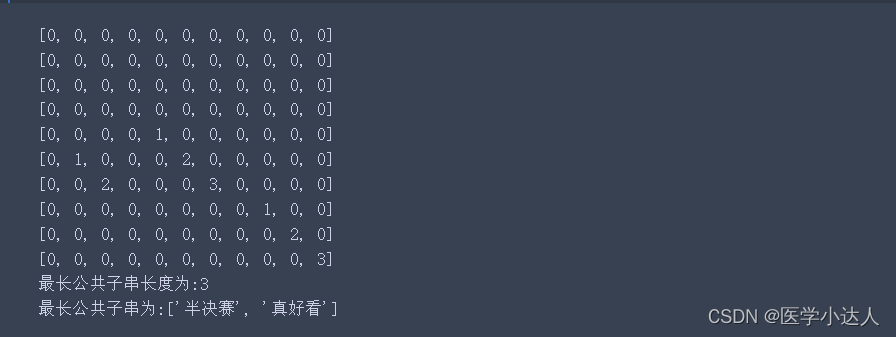

 动态规划策略：动态规划中本阶段的状态往往是上一阶段状态和上一阶段决策的结果。若给定了第K阶段的状态Sk以及决策uk(Sk),则第K+1阶段的状态Sk+1也就完全确定。也就是说Sk+1与Sk,uk之间存在一种明确的数量对应关系，记为Tk(Sk,uk),即有Sk+1= Tk(Sk,uk)。 这种用函数表示前后阶段关系的方程，称为状态转移方程。在上例中状态转移方程为 Sk+1= uk(Sk) 。

转移方程：

 2.例子2：背包空间问题，即组合最优化问题？

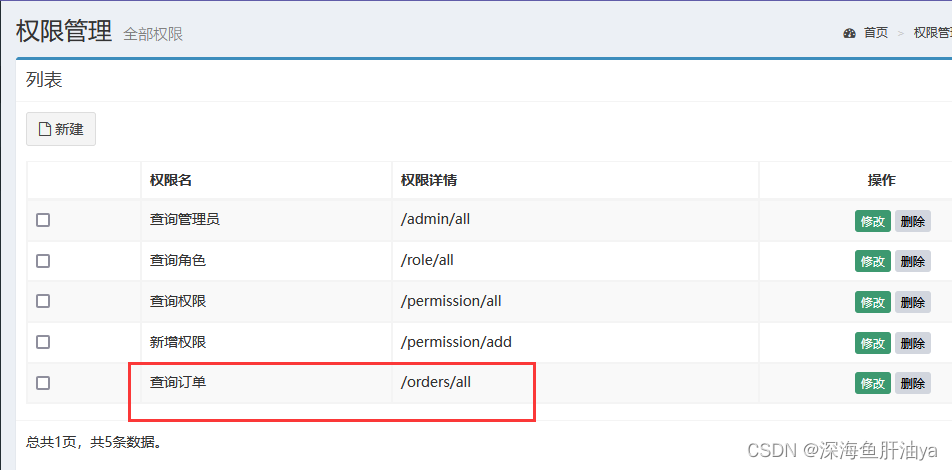
假设王同学要去野营，他准备了以下物品：

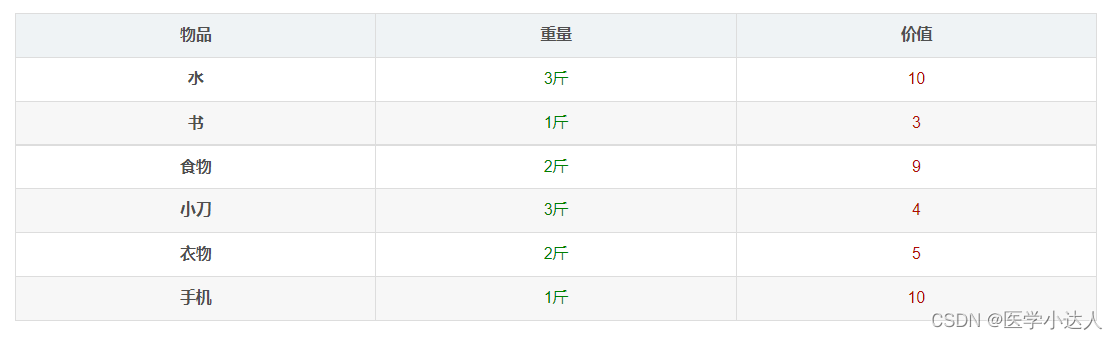
背包最大容量为6斤，装不下所有的东西，只能从这堆东西中挑选组合价值最高的物品，这是典型的最优组合问题：

方法一：

思路：构建一个解题矩阵，（物品）*（背包空间），然后计算每个矩阵位点的最优解，即价值最大组合。

代码;

#完整代码
def dynamic_p() -> list:
    items = [  									 # 物品项
        {"name": "水", "weight": 3, "value": 10},
        {"name": "书", "weight": 1, "value": 3},
        {"name": "食物", "weight": 2, "value": 9},
        {"name": "小刀", "weight": 3, "value": 4},
        {"name": "衣物", "weight": 2, "value": 5},
        {"name": "手机", "weight": 1, "value": 10}
    ]
    max_capacity = 6                             # 约束条件为 背包最大承重为6
    dp = [[0] * (max_capacity + 1) for _ in range(len(items) + 1)]

    for row in range(1, len(items) + 1):         # row 代表行
        for col in range(1, max_capacity + 1):   # col 代表列
            weight = items[row - 1]["weight"]    # 获取当前物品重量
            value = items[row - 1]["value"]      # 获取当前物品价值
            if weight > col:                     # 判断物品重量是否大于当前背包容量
                dp[row][col] = dp[row - 1][col]  # 大于直接取上一次最优结果 此时row-1代表上一行
            else:
                # row-1 为上一行，row为本行，若要重复拿取，只需要在目前物品所在的那一行寻找最优解即可
                dp[row][col] = max(value + dp[row][col - weight], dp[row - 1][col])
    return dp


dp = dynamic_p()
for i in dp:                                     # 打印数组
    print(i)

print(dp[-1][-1])                                # 打印最优解的价值和

方法二：通过平均最大价值来计算

思路：构建物品矩阵，计算每件物品的平均价值，选取最优的放进包里

import numpy as np

items = [  									 # 物品项
        {"name": "水", "weight": 3, "value": 10},
        {"name": "书", "weight": 1, "value": 3},
        {"name": "食物", "weight": 2, "value": 9},
        {"name": "小刀", "weight": 3, "value": 4},
        {"name": "衣物", "weight": 2, "value": 5},
        {"name": "手机", "weight": 1, "value": 10}
    ]

#物品词典
dic_name ={i['name']:index for index,i in enumerate(items)}
#构建item矩阵
item2array = np.zeros((6,4),dtype='float')
for i,j in enumerate(items):
    item2array[i][0] = float(dic_name.get(j['name']))
    item2array[i][1] = float(j['weight'])
    item2array[i][2] = float(j['value'])
    item2array[i][3] = item2array[i][2]/item2array[i][1]

#矩阵排序
item2array_01 = item2array[np.lexsort(-item2array.T)]

#剩余空间v_remain
v_remain = 6
#目前背包中物品的价值value
value = 0
#背包中的物品re_lis
re_lis = []
for i in item2array_01:
    if i[1] <= v_remain:
        v_remain = v_remain - i[1]
        value = value + i[2]
        for m in dic_name.keys():
            if float(dic_name[m]) == float(i[0]):
                re_lis.append(m)
print(v_remain,value,re_lis)

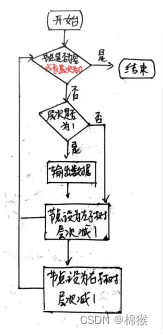
例子3：斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34...

斐波纳契数列转移方程可以写成：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）
方法1：

def febonaci(n):
    a,b = 0,1
    for i in range(n):
        a,b = b,a+b
        print(a)
febonaci(5)

 方法2：

def febonaci(n):
    a,b =0,1
    i = 0
    while i < n:
        print(a)
        a,b = b,a+b
        i+=1

方法3： 

def febonaci(n):
    lis_num = []
    for i in range(n):
        if i==0 or i==1:
            lis_num.append(i)
        else:
            lis_num.append(lis_num[-1]+lis_num[-2])
    return lis_num

 方法4： 

def febonaci(n):
    lis_num = []
    i = 0
    while i < n:
        if i==0 or i==1:
            lis_num.append(i)
        else:
            lis_num.append(lis_num[-1]+lis_num[-2])
        i += 1
    return lis_num

  方法5： 

def febonaci(n):
    def feb(i):
        if i<2:
            return i
        else:
            return feb(i-1)+feb(i-2)
    for i in range(n):
        print(feb(i))

 其中方法345可以直观的看到状态转移方程。

参考：Python 算法之 动态规划详解_XianZhe_的博客-CSDN博客_python 动态规划